1. 下列选项中,$\angle 1与\angle 2$是对顶角的是 (
B
)答案:B
解析:
根据对顶角的定义:两条直线相交后所得的只有一个公共顶点且两边互为反向延长线的两个角叫做对顶角。
观察各选项:
选项A、C、D中,∠1与∠2的两边不互为反向延长线,不符合对顶角定义。
选项B中,两条直线相交,∠1与∠2有公共顶点,且两边互为反向延长线,符合对顶角定义。
答案:B
观察各选项:
选项A、C、D中,∠1与∠2的两边不互为反向延长线,不符合对顶角定义。
选项B中,两条直线相交,∠1与∠2有公共顶点,且两边互为反向延长线,符合对顶角定义。
答案:B
2. 已知点$A,B,C,D,E$的位置如图所示,下列结论中正确的是 (
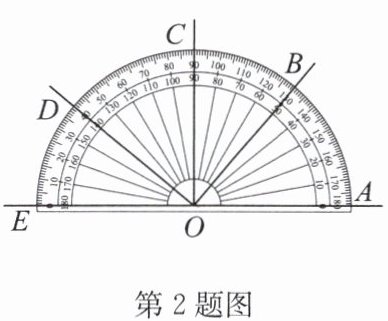
A.$\angle AOB= 130^{\circ}$
B.$\angle DOC与\angle BOE$互补
C.$\angle AOB= \angle DOE$
D.$\angle AOB与\angle COD$互余
B
)
A.$\angle AOB= 130^{\circ}$
B.$\angle DOC与\angle BOE$互补
C.$\angle AOB= \angle DOE$
D.$\angle AOB与\angle COD$互余
答案:B
解析:
由图可知:
$\angle AOB=20^{\circ}$,A选项错误;
$\angle DOC=50^{\circ}$,$\angle BOE=130^{\circ}$,$50^{\circ}+130^{\circ}=180^{\circ}$,所以$\angle DOC$与$\angle BOE$互补,B选项正确;
$\angle DOE=40^{\circ}$,$\angle AOB=20^{\circ}$,C选项错误;
$\angle COD=50^{\circ}$,$\angle AOB=20^{\circ}$,$50^{\circ}+20^{\circ}=70^{\circ}\neq90^{\circ}$,D选项错误。
B
$\angle AOB=20^{\circ}$,A选项错误;
$\angle DOC=50^{\circ}$,$\angle BOE=130^{\circ}$,$50^{\circ}+130^{\circ}=180^{\circ}$,所以$\angle DOC$与$\angle BOE$互补,B选项正确;
$\angle DOE=40^{\circ}$,$\angle AOB=20^{\circ}$,C选项错误;
$\angle COD=50^{\circ}$,$\angle AOB=20^{\circ}$,$50^{\circ}+20^{\circ}=70^{\circ}\neq90^{\circ}$,D选项错误。
B
3. (2024·启东期末)如图,直线$AB,CD相交于点O$,$\angle DOE= 90^{\circ}$,$\angle 1= 40^{\circ}$,则$\angle AOC$的度数为
$130^{\circ}$
.答案:$ 130^{\circ} $
4. 如图,当剪刀口$\angle AOB增大21^{\circ}$时,$\angle COD$增大
$ 21^{\circ} $
.答案:$ 21^{\circ} $
解析:
解:由对顶角相等可知,∠AOB = ∠COD。当∠AOB增大21°时,∠COD也增大21°。
21°
21°
5. 如图,直线$AB,CD相交于点O$,$\angle AOC= 40^{\circ}$,$OE平分\angle BOC$,求$\angle DOE$的度数.


答案:解:因为 $ \angle AOC = 40^{\circ} $,所以 $ \angle BOC = 180^{\circ} - \angle AOC = 140^{\circ} $。因为 $ OE $ 平分 $ \angle BOC $,所以 $ \angle BOE = \frac{1}{2} \angle BOC = 70^{\circ} $。因为 $ \angle BOD = \angle AOC = 40^{\circ} $,所以 $ \angle DOE = \angle BOD + \angle BOE = 40^{\circ} + 70^{\circ} = 110^{\circ} $。
解析:
解:因为直线$AB$,$CD$相交于点$O$,$\angle AOC = 40^{\circ}$,
所以$\angle BOC = 180^{\circ}-\angle AOC = 180^{\circ}-40^{\circ}=140^{\circ}$。
因为$OE$平分$\angle BOC$,
所以$\angle BOE=\frac{1}{2}\angle BOC=\frac{1}{2}×140^{\circ}=70^{\circ}$。
因为$\angle BOD$与$\angle AOC$是对顶角,
所以$\angle BOD=\angle AOC = 40^{\circ}$。
所以$\angle DOE=\angle BOD+\angle BOE=40^{\circ}+70^{\circ}=110^{\circ}$。
所以$\angle BOC = 180^{\circ}-\angle AOC = 180^{\circ}-40^{\circ}=140^{\circ}$。
因为$OE$平分$\angle BOC$,
所以$\angle BOE=\frac{1}{2}\angle BOC=\frac{1}{2}×140^{\circ}=70^{\circ}$。
因为$\angle BOD$与$\angle AOC$是对顶角,
所以$\angle BOD=\angle AOC = 40^{\circ}$。
所以$\angle DOE=\angle BOD+\angle BOE=40^{\circ}+70^{\circ}=110^{\circ}$。
6. 如图,直线$AB,CD,EF相交于点O$,已知$OA平分\angle EOC$,若$\angle EOC:\angle EOD= 2:3$,则$\angle BOD$的度数为 (
A.$40^{\circ}$
B.$37^{\circ}$
C.$36^{\circ}$
D.$35^{\circ}$
C
)A.$40^{\circ}$
B.$37^{\circ}$
C.$36^{\circ}$
D.$35^{\circ}$
答案:C
解析:
解:设∠EOC=2x,∠EOD=3x。
∵∠EOC+∠EOD=180°,
∴2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°。
∵OA平分∠EOC,
∴∠AOE=∠AOC=∠EOC/2=36°。
∵∠BOD=∠AOC(对顶角相等),
∴∠BOD=36°。
答案:C
∵∠EOC+∠EOD=180°,
∴2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°。
∵OA平分∠EOC,
∴∠AOE=∠AOC=∠EOC/2=36°。
∵∠BOD=∠AOC(对顶角相等),
∴∠BOD=36°。
答案:C
7. 如图,三条直线$a,b,c$相交于一点,则$\angle 1+\angle 2+\angle 3= $ (

A.$360^{\circ}$
B.$180^{\circ}$
C.$120^{\circ}$
D.$90^{\circ}$
B
)
A.$360^{\circ}$
B.$180^{\circ}$
C.$120^{\circ}$
D.$90^{\circ}$
答案:B
解析:
解:由对顶角相等可知,∠2的对顶角与∠1、∠3组成一个平角。
因为平角为180°,所以∠1+∠2+∠3=180°。
答案:B
因为平角为180°,所以∠1+∠2+∠3=180°。
答案:B
8. 两条直线相交所成的四个角中,有两个角分别是$(2x - 10)^{\circ}和(110 - x)^{\circ}$,则$x= $
40 或 80
.答案:40 或 80
解析:
解:两条直线相交所成的四个角中,对顶角相等,邻补角互补。
情况一:若两角为对顶角,则$2x - 10 = 110 - x$
$2x + x = 110 + 10$
$3x = 120$
$x = 40$
情况二:若两角为邻补角,则$(2x - 10) + (110 - x) = 180$
$2x - 10 + 110 - x = 180$
$x + 100 = 180$
$x = 80$
综上,$x = 40$或$80$。
情况一:若两角为对顶角,则$2x - 10 = 110 - x$
$2x + x = 110 + 10$
$3x = 120$
$x = 40$
情况二:若两角为邻补角,则$(2x - 10) + (110 - x) = 180$
$2x - 10 + 110 - x = 180$
$x + 100 = 180$
$x = 80$
综上,$x = 40$或$80$。