9. 两条直线相交于点$O$,共有
2
对对顶角;三条直线相交于点$O$,共有6
对对顶角;$n条直线相交于点O$,共有$n(n - 1)$
对对顶角.答案:2 6 $ n(n - 1) $
解析:
两条直线相交于点$O$,形成$2$对对顶角;三条直线相交于点$O$,形成$6$对对顶角;$n$条直线相交于点$O$,共有$n(n - 1)$对对顶角。
答案依次为:$2$;$6$;$n(n - 1)$
答案依次为:$2$;$6$;$n(n - 1)$
10. 如图,点$A,O,B$在同一条直线上,$OE平分\angle BOC$,$\angle DOE= 90^{\circ}$.
(1)与$\angle COD$互余的角有
(2)若$\angle COE= 30^{\circ}$,求$\angle AOE$的度数;
(3)试说明:$OD是\angle AOC$的平分线.
(1)与$\angle COD$互余的角有
$ \angle BOE $,$ \angle COE $
;(2)若$\angle COE= 30^{\circ}$,求$\angle AOE$的度数;
解:因为 $ OE $ 平分 $ \angle BOC $,所以 $ \angle COE = \angle BOE = 30^{\circ} $,所以 $ \angle AOE = 180^{\circ} - 30^{\circ} = 150^{\circ} $
(3)试说明:$OD是\angle AOC$的平分线.
解:因为 $ OE $ 是 $ \angle BOC $ 的平分线,所以 $ \angle COE = \angle BOE $。因为 $ \angle DOE = 90^{\circ} $,所以 $ \angle COD + \angle COE = 90^{\circ} $,且 $ \angle DOA + \angle BOE = 180^{\circ} - \angle DOE = 90^{\circ} $,所以 $ \angle DOC + \angle COE = \angle DOA + \angle BOE $,所以 $ \angle DOC = \angle DOA $,所以 $ OD $ 是 $ \angle AOC $ 的平分线。
答案:(1) $ \angle BOE $,$ \angle COE $;(2) 解:因为 $ OE $ 平分 $ \angle BOC $,所以 $ \angle COE = \angle BOE = 30^{\circ} $,所以 $ \angle AOE = 180^{\circ} - 30^{\circ} = 150^{\circ} $;(3) 解:因为 $ OE $ 是 $ \angle BOC $ 的平分线,所以 $ \angle COE = \angle BOE $。因为 $ \angle DOE = 90^{\circ} $,所以 $ \angle COD + \angle COE = 90^{\circ} $,且 $ \angle DOA + \angle BOE = 180^{\circ} - \angle DOE = 90^{\circ} $,所以 $ \angle DOC + \angle COE = \angle DOA + \angle BOE $,所以 $ \angle DOC = \angle DOA $,所以 $ OD $ 是 $ \angle AOC $ 的平分线。
解析:
(1) $\angle BOE$,$\angle COE$
(2) 解:因为 $OE$ 平分 $\angle BOC$,所以 $\angle COE = \angle BOE = 30^{\circ}$,所以 $\angle AOE = 180^{\circ} - \angle BOE = 180^{\circ} - 30^{\circ} = 150^{\circ}$
(3) 证明:因为 $OE$ 平分 $\angle BOC$,所以 $\angle COE = \angle BOE$。因为 $\angle DOE = 90^{\circ}$,所以 $\angle COD + \angle COE = 90^{\circ}$。因为点 $A, O, B$ 在同一条直线上,所以 $\angle AOB = 180^{\circ}$,所以 $\angle AOD + \angle DOE + \angle BOE = 180^{\circ}$,即 $\angle AOD + 90^{\circ} + \angle BOE = 180^{\circ}$,所以 $\angle AOD + \angle BOE = 90^{\circ}$。因为 $\angle COD + \angle COE = 90^{\circ}$ 且 $\angle COE = \angle BOE$,所以 $\angle COD = \angle AOD$,所以 $OD$ 是 $\angle AOC$ 的平分线。
(2) 解:因为 $OE$ 平分 $\angle BOC$,所以 $\angle COE = \angle BOE = 30^{\circ}$,所以 $\angle AOE = 180^{\circ} - \angle BOE = 180^{\circ} - 30^{\circ} = 150^{\circ}$
(3) 证明:因为 $OE$ 平分 $\angle BOC$,所以 $\angle COE = \angle BOE$。因为 $\angle DOE = 90^{\circ}$,所以 $\angle COD + \angle COE = 90^{\circ}$。因为点 $A, O, B$ 在同一条直线上,所以 $\angle AOB = 180^{\circ}$,所以 $\angle AOD + \angle DOE + \angle BOE = 180^{\circ}$,即 $\angle AOD + 90^{\circ} + \angle BOE = 180^{\circ}$,所以 $\angle AOD + \angle BOE = 90^{\circ}$。因为 $\angle COD + \angle COE = 90^{\circ}$ 且 $\angle COE = \angle BOE$,所以 $\angle COD = \angle AOD$,所以 $OD$ 是 $\angle AOC$ 的平分线。
11. 如图①,直线$AB与CD相交于点E$,射线$EG在\angle AEC$内部.
(1)若$\angle BEC$的补角是它的余角的3倍,则$\angle BEC= $
(2)在(1)的条件下,若$\angle CEG比\angle AEG小25^{\circ}$,求$\angle AEG$的度数;
(3)如图②,若射线$EF平分\angle AED$,$\angle FEG= 100^{\circ}$,则$\angle AEG-\angle CEG= $
(1)若$\angle BEC$的补角是它的余角的3倍,则$\angle BEC= $
$45^{\circ}$
;(2)在(1)的条件下,若$\angle CEG比\angle AEG小25^{\circ}$,求$\angle AEG$的度数;
解:因为 $ \angle BEC = 45^{\circ} $,所以 $ \angle AEC = 135^{\circ} $。设 $ \angle AEG = x^{\circ} $,则 $ \angle CEG = x^{\circ} - 25^{\circ} $,所以 $ x + (x - 25) = 135 $,解得 $ x = 80 $,所以 $ \angle AEG = 80^{\circ} $
(3)如图②,若射线$EF平分\angle AED$,$\angle FEG= 100^{\circ}$,则$\angle AEG-\angle CEG= $
$20^{\circ}$
.答案:(1) $ 45^{\circ} $;(2) 解:因为 $ \angle BEC = 45^{\circ} $,所以 $ \angle AEC = 135^{\circ} $。设 $ \angle AEG = x^{\circ} $,则 $ \angle CEG = x^{\circ} - 25^{\circ} $,所以 $ x + (x - 25) = 135 $,解得 $ x = 80 $,所以 $ \angle AEG = 80^{\circ} $;(3) $ 20^{\circ} $
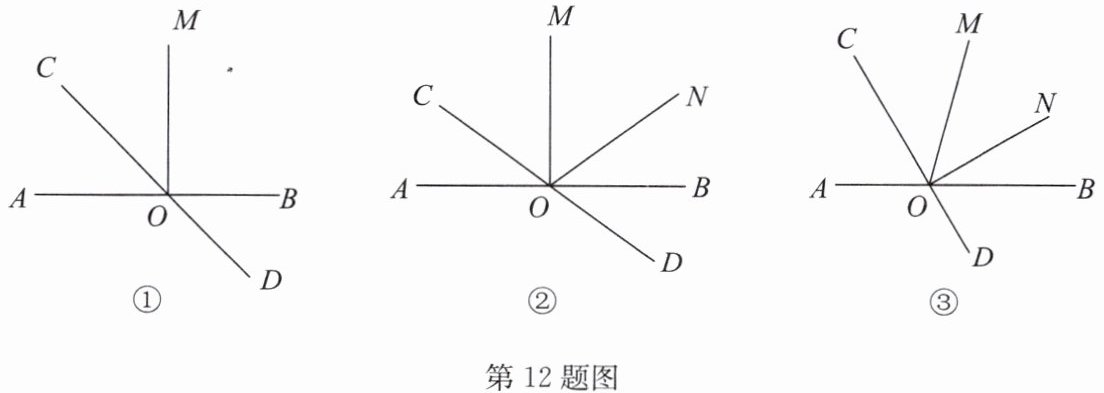
12. 如图,直线$AB与CD相交于点O$.
(1)如图①,若$\angle AOM= 90^{\circ}$,$OC平分\angle AOM$,求$\angle AOD$的度数;
(2)如图②,若$\angle AOM= 90^{\circ}$,$\angle BOC= 4\angle BON$,$OM平分\angle CON$,求$\angle MON$的度数;
(3)如图③,若$\angle AOM= \alpha$,$\angle BOC= 4\angle BON$,$OM平分\angle CON$,求$\angle MON$的度数. (用含$\alpha$的式子表示)
(1)如图①,若$\angle AOM= 90^{\circ}$,$OC平分\angle AOM$,求$\angle AOD$的度数;
(2)如图②,若$\angle AOM= 90^{\circ}$,$\angle BOC= 4\angle BON$,$OM平分\angle CON$,求$\angle MON$的度数;
(3)如图③,若$\angle AOM= \alpha$,$\angle BOC= 4\angle BON$,$OM平分\angle CON$,求$\angle MON$的度数. (用含$\alpha$的式子表示)

答案:(1) 解:因为 $ \angle AOM = 90^{\circ} $,$ OC $ 平分 $ \angle AOM $,所以 $ \angle AOC = \frac{1}{2} \angle AOM = \frac{1}{2} × 90^{\circ} = 45^{\circ} $。因为 $ \angle AOC + \angle AOD = 180^{\circ} $,所以 $ \angle AOD = 180^{\circ} - \angle AOC = 180^{\circ} - 45^{\circ} = 135^{\circ} $;(2) 解:因为 $ \angle BOC = 4 \angle BON $,所以设 $ \angle BON = x $,则 $ \angle BOC = 4x $,所以 $ \angle CON = \angle COB - \angle BON = 4x - x = 3x $。因为 $ OM $ 平分 $ \angle CON $,所以 $ \angle COM = \angle MON = \frac{1}{2} \angle CON = \frac{3}{2}x $。因为 $ \angle AOM = 90^{\circ} $,所以 $ \angle BOM = 90^{\circ} $,所以 $ \angle BOM = \angle MON + \angle BON = \frac{3}{2}x + x = 90^{\circ} $,所以 $ x = 36^{\circ} $,所以 $ \angle MON = \frac{3}{2}x = \frac{3}{2} × 36^{\circ} = 54^{\circ} $;(3) 解:因为 $ \angle BOC = 4 \angle BON $,所以设 $ \angle BON = x $,则 $ \angle BOC = 4x $,由 (2) 可知 $ \angle COM = \angle MON = \frac{1}{2} \angle CON = \frac{3}{2}x $。因为 $ \angle AOM = \alpha $,所以 $ \angle BOM = \angle MON + \angle BON = \frac{3}{2}x + x = 180^{\circ} - \alpha $,所以 $ x = \frac{360^{\circ} - 2\alpha}{5} $,所以 $ \angle MON = \frac{3}{2}x = \frac{3}{2} × \frac{360^{\circ} - 2\alpha}{5} = \frac{540^{\circ} - 3\alpha}{5} $
解析:
(1) 解:因为 $ \angle AOM = 90^{\circ} $,$ OC $ 平分 $ \angle AOM $,所以 $ \angle AOC = \frac{1}{2} \angle AOM = \frac{1}{2} × 90^{\circ} = 45^{\circ} $。因为 $ \angle AOC + \angle AOD = 180^{\circ} $,所以 $ \angle AOD = 180^{\circ} - 45^{\circ} = 135^{\circ} $。
(2) 解:设 $ \angle BON = x $,则 $ \angle BOC = 4x $,所以 $ \angle CON = \angle BOC - \angle BON = 4x - x = 3x $。因为 $ OM $ 平分 $ \angle CON $,所以 $ \angle MON = \frac{1}{2} \angle CON = \frac{3}{2}x $。因为 $ \angle AOM = 90^{\circ} $,所以 $ \angle BOM = 180^{\circ} - \angle AOM = 90^{\circ} $。又因为 $ \angle BOM = \angle MON + \angle BON $,所以 $ \frac{3}{2}x + x = 90^{\circ} $,解得 $ x = 36^{\circ} $,所以 $ \angle MON = \frac{3}{2} × 36^{\circ} = 54^{\circ} $。
(3) 解:设 $ \angle BON = x $,则 $ \angle BOC = 4x $,所以 $ \angle CON = 4x - x = 3x $。因为 $ OM $ 平分 $ \angle CON $,所以 $ \angle MON = \frac{3}{2}x $。因为 $ \angle AOM = \alpha $,所以 $ \angle BOM = 180^{\circ} - \alpha $。又因为 $ \angle BOM = \angle MON + \angle BON $,所以 $ \frac{3}{2}x + x = 180^{\circ} - \alpha $,解得 $ x = \frac{2(180^{\circ} - \alpha)}{5} = \frac{360^{\circ} - 2\alpha}{5} $,所以 $ \angle MON = \frac{3}{2} × \frac{360^{\circ} - 2\alpha}{5} = \frac{540^{\circ} - 3\alpha}{5} $。
(2) 解:设 $ \angle BON = x $,则 $ \angle BOC = 4x $,所以 $ \angle CON = \angle BOC - \angle BON = 4x - x = 3x $。因为 $ OM $ 平分 $ \angle CON $,所以 $ \angle MON = \frac{1}{2} \angle CON = \frac{3}{2}x $。因为 $ \angle AOM = 90^{\circ} $,所以 $ \angle BOM = 180^{\circ} - \angle AOM = 90^{\circ} $。又因为 $ \angle BOM = \angle MON + \angle BON $,所以 $ \frac{3}{2}x + x = 90^{\circ} $,解得 $ x = 36^{\circ} $,所以 $ \angle MON = \frac{3}{2} × 36^{\circ} = 54^{\circ} $。
(3) 解:设 $ \angle BON = x $,则 $ \angle BOC = 4x $,所以 $ \angle CON = 4x - x = 3x $。因为 $ OM $ 平分 $ \angle CON $,所以 $ \angle MON = \frac{3}{2}x $。因为 $ \angle AOM = \alpha $,所以 $ \angle BOM = 180^{\circ} - \alpha $。又因为 $ \angle BOM = \angle MON + \angle BON $,所以 $ \frac{3}{2}x + x = 180^{\circ} - \alpha $,解得 $ x = \frac{2(180^{\circ} - \alpha)}{5} = \frac{360^{\circ} - 2\alpha}{5} $,所以 $ \angle MON = \frac{3}{2} × \frac{360^{\circ} - 2\alpha}{5} = \frac{540^{\circ} - 3\alpha}{5} $。