1. 下列图形中,线段PQ的长表示点P到直线MN的距离的是 (
A
)答案:A
解析:
点到直线的距离是指从点向直线作垂线,垂线段的长度。观察各选项:
选项A中,PQ垂直于MN,且Q在MN上,PQ为垂线段,其长度表示点P到直线MN的距离。
选项B中,PQ垂直于某条直线,但垂足不在MN上,不符合定义。
选项C中,PQ与MN不垂直,不是垂线段。
选项D中,点P在直线MN上,距离为0,PQ不表示距离。
A
选项A中,PQ垂直于MN,且Q在MN上,PQ为垂线段,其长度表示点P到直线MN的距离。
选项B中,PQ垂直于某条直线,但垂足不在MN上,不符合定义。
选项C中,PQ与MN不垂直,不是垂线段。
选项D中,点P在直线MN上,距离为0,PQ不表示距离。
A
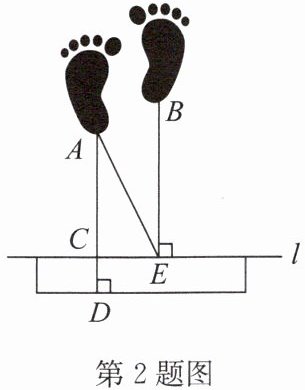
2. (2024·启东期中)如图,在测量跳远成绩的示意图中,直线l是起跳线,则需要测量的线段是 (
A.AE
B.AC
C.AD
D.BE
B
)
A.AE
B.AC
C.AD
D.BE
答案:B
解析:
根据跳远成绩测量规则,成绩为起跳线到落点最近点的垂线段长度。图中直线$l$是起跳线,落点为$A$、$B$,其中$AC$是点$A$到直线$l$的垂线段,且为最近距离。
B
B
3. (2024·鼓楼区月考)如图,河道的一侧有甲、乙两个村庄,现要铺设一条管道将水引向甲、乙两村,下列四种方案中最节省材料的是 (

B
)
答案:B
解析:
要节省材料即需使管道总长度最短。根据“两点之间线段最短”及“垂线段最短”的原理,方案B中从甲村到乙村为线段,从乙村到河道为垂线段,总长度最短。
B
B
4. 如图,$AB⊥直线l_{1},AC⊥直线l_{2}$,垂足分别为B和A,则点A到直线$l_{1}$的距离是线段
AB
的长度.答案:AB
5. (1)利用直尺在如图的网格中完成下列操作:①经过点A画直线PA垂直于AB;②经过点C画直线CM垂直于CD;
(2)用符号表示上面①,②中的垂直关系.

(2)用符号表示上面①,②中的垂直关系.

答案:
解:(1)如答图,直线PA,CM即为所求. (2)PA⊥AB,MC⊥CD.
解:(1)如答图,直线PA,CM即为所求. (2)PA⊥AB,MC⊥CD.

6. 若P为直线l外一定点,A为直线l上一定点,且$PA= 2$,点P到直线l的距离为d,则d的取值范围为 (
A.$0<d<2$
B.$d≥2$
C.$0≤d<2$
D.$0<d≤2$
D
)A.$0<d<2$
B.$d≥2$
C.$0≤d<2$
D.$0<d≤2$
答案:D
解析:
解:点P到直线l的距离d是点P到直线l的垂线段的长度。
因为PA是点P到直线l上一点A的线段,且PA=2,根据垂线段最短的性质,可知d≤PA,即d≤2。
又因为P为直线l外一定点,所以点P到直线l的距离d不能为0(若d=0,则点P在直线l上,与已知矛盾),故d>0。
综上,d的取值范围为0<d≤2。
答案:D
因为PA是点P到直线l上一点A的线段,且PA=2,根据垂线段最短的性质,可知d≤PA,即d≤2。
又因为P为直线l外一定点,所以点P到直线l的距离d不能为0(若d=0,则点P在直线l上,与已知矛盾),故d>0。
综上,d的取值范围为0<d≤2。
答案:D