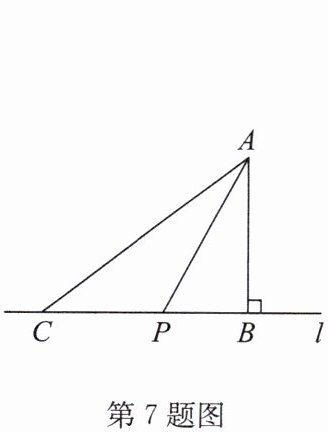
7. 如图,A是直线l外一点,过点A作$AB⊥$直线l于点B.在直线l上取一点C,连接AC,使$AC= \frac {5}{3}AB$.点P在线段BC上,连接AP.若$AB= 3$,则线段AP的长不可能是 (
A.3.5
B.4
C.5
D.5.5
D
)
A.3.5
B.4
C.5
D.5.5
答案:D
解析:
解:
∵ $AB \perp$ 直线 $l$,$AB = 3$,
∴ $AB$ 是点 $A$ 到直线 $l$ 的垂线段,$AP$ 为斜线段时 $AP > AB$。
∵ $AC = \frac{5}{3}AB$,
∴ $AC = \frac{5}{3} × 3 = 5$。
点 $P$ 在线段 $BC$ 上,
∴ $AB \leq AP \leq AC$,即 $3 \leq AP \leq 5$。
∴ $AP$ 的长不可能是 $5.5$。
答案:D
∵ $AB \perp$ 直线 $l$,$AB = 3$,
∴ $AB$ 是点 $A$ 到直线 $l$ 的垂线段,$AP$ 为斜线段时 $AP > AB$。
∵ $AC = \frac{5}{3}AB$,
∴ $AC = \frac{5}{3} × 3 = 5$。
点 $P$ 在线段 $BC$ 上,
∴ $AB \leq AP \leq AC$,即 $3 \leq AP \leq 5$。
∴ $AP$ 的长不可能是 $5.5$。
答案:D
8. 如图,某单位要在河岸l上建一个水泵房引水到C处.他们的做法是:过点C作$CD⊥l$于点D,将水泵房建在了D处.这样做最节省水管,其数学道理是

垂线段最短
.
答案:垂线段最短
9. 如图,在直角三角形ABC中,$∠BAC= 90^{\circ },AB= 6cm,AC= 8cm,BC= 10cm$,则点A到边BC的距离为

4.8
cm.
答案:4.8
解析:
解:设点A到边BC的距离为h cm。
因为在直角三角形ABC中,∠BAC=90°,AB=6cm,AC=8cm,
所以三角形ABC的面积为:$\frac{1}{2} × AB × AC = \frac{1}{2} × 6 × 8 = 24$($cm^2$)。
又因为BC=10cm,三角形面积也可表示为$\frac{1}{2} × BC × h$,
所以$\frac{1}{2} × 10 × h = 24$,
解得$h = 4.8$。
4.8
因为在直角三角形ABC中,∠BAC=90°,AB=6cm,AC=8cm,
所以三角形ABC的面积为:$\frac{1}{2} × AB × AC = \frac{1}{2} × 6 × 8 = 24$($cm^2$)。
又因为BC=10cm,三角形面积也可表示为$\frac{1}{2} × BC × h$,
所以$\frac{1}{2} × 10 × h = 24$,
解得$h = 4.8$。
4.8
10. 如图,在直线MN的异侧有A,B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是______.
(2)在直线MN上取一点D,使线段$AD+BD$最短.依据是______.

(1)在直线MN上取一点C,使线段AC最短.依据是______.
(2)在直线MN上取一点D,使线段$AD+BD$最短.依据是______.

答案:
解:(1)如答图,过点A作AC⊥MN于点C. 垂线段最短 (2)如答图,连接AB交MN于点D. 两点之间,线段最短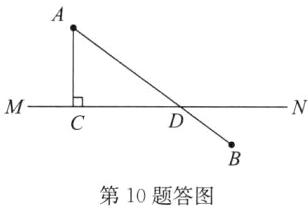
解:(1)如答图,过点A作AC⊥MN于点C. 垂线段最短 (2)如答图,连接AB交MN于点D. 两点之间,线段最短

11. 如图,O是直线AB,CD的交点,$OE⊥AB,OF⊥CD$,OM是$∠BOF$的平分线.
(1)填空:
①由OM是$∠BOF$的平分线,可得$∠FOM= ∠$
②若$∠AOC= 34^{\circ }$,则$∠BOD= $
③根据
(2)若$∠AOC= α$,求$∠COM$的度数.(用含α的代数式表示)

(1)填空:
①由OM是$∠BOF$的平分线,可得$∠FOM= ∠$
BOM
;②若$∠AOC= 34^{\circ }$,则$∠BOD= $
34°
;③根据
同角的余角相等
,可得$∠EOF= ∠AOC$.(2)若$∠AOC= α$,求$∠COM$的度数.(用含α的代数式表示)

解:因为∠AOC=α,所以∠BOD=∠AOC=α.因为OF⊥CD,所以∠DOF=90°,所以∠BOF=∠DOF−∠BOD=90°−α.因为OM是∠BOF的平分线,所以∠MOF=$\frac{1}{2}$∠BOF=$\frac{1}{2}$(90°−α)=45°−$\frac{1}{2}$α.因为OF⊥CD,所以∠COF=90°,所以∠COM=∠COF+∠MOF=90°+45°−$\frac{1}{2}$α=135°−$\frac{1}{2}$α.
答案:(1)①BOM ②34° ③同角的余角相等 (2)解:因为∠AOC=α,所以∠BOD=∠AOC=α.因为OF⊥CD,所以∠DOF=90°,所以∠BOF=∠DOF−∠BOD=90°−α.因为OM是∠BOF的平分线,所以∠MOF=$\frac{1}{2}$∠BOF=$\frac{1}{2}$(90°−α)=45°−$\frac{1}{2}$α.因为OF⊥CD,所以∠COF=90°,所以∠COM=∠COF+∠MOF=90°+45°−$\frac{1}{2}$α=135°−$\frac{1}{2}$α.