7. 已知点$A$,$B$,$C$在同一条直线上,若$AC = 8$,$BC = 6$,$D$是$AC$的中点,则$BD$的长为
10 或 2
。答案:10 或 2
解析:
解:
情况一:点B在AC的延长线上
∵D是AC的中点,AC=8
∴CD=AC/2=4
∴BD=CD+BC=4+6=10
情况二:点B在AC上
∵D是AC的中点,AC=8
∴CD=AC/2=4
∵BC=6,AC=8,6<8
∴点B在AC上且靠近C点
∴BD=BC-CD=6-4=2
综上,BD的长为10或2。
情况一:点B在AC的延长线上
∵D是AC的中点,AC=8
∴CD=AC/2=4
∴BD=CD+BC=4+6=10
情况二:点B在AC上
∵D是AC的中点,AC=8
∴CD=AC/2=4
∵BC=6,AC=8,6<8
∴点B在AC上且靠近C点
∴BD=BC-CD=6-4=2
综上,BD的长为10或2。
8. 如图,$∠AOB = 150^{\circ}$,$∠COD = 40^{\circ}$,$OE$平分$∠AOC$,则$2∠BOE - ∠BOD =$
$110^{\circ}$
。答案:$ 110^{\circ} $
解析:
设∠BOC = x,
∵∠AOB = 150°,
∴∠AOC = ∠AOB - ∠BOC = 150° - x,
∵OE平分∠AOC,
∴∠COE = 1/2∠AOC = 1/2(150° - x) = 75° - x/2,
∵∠COD = 40°,
∴∠BOD = ∠COD - ∠BOC = 40° - x,
∠BOE = ∠COE + ∠BOC = 75° - x/2 + x = 75° + x/2,
2∠BOE - ∠BOD = 2(75° + x/2) - (40° - x) = 150° + x - 40° + x = 110° + 2x - x = 110°。
110°
∵∠AOB = 150°,
∴∠AOC = ∠AOB - ∠BOC = 150° - x,
∵OE平分∠AOC,
∴∠COE = 1/2∠AOC = 1/2(150° - x) = 75° - x/2,
∵∠COD = 40°,
∴∠BOD = ∠COD - ∠BOC = 40° - x,
∠BOE = ∠COE + ∠BOC = 75° - x/2 + x = 75° + x/2,
2∠BOE - ∠BOD = 2(75° + x/2) - (40° - x) = 150° + x - 40° + x = 110° + 2x - x = 110°。
110°
9. 如图,如果$∠1 = ∠EDF$,那么可得
AB
$//$DF
;如果$∠2 = ∠EDF$,那么可得BC
$//$ED
。答案:AB DF BC ED
解析:
如果$∠1 = ∠EDF$,那么可得$AB// DF$;如果$∠2 = ∠EDF$,那么可得$BC// ED$。
10. 如图,以$O$为端点画六条射线$OA$,$OB$,$OC$,$OD$,$OE$,$OF$,再从射线$OA$上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为$1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$\cdots$,那么所描的第$2025$个点在射线
OC
上。答案:OC
解析:
解:由题意可知,点的序号按逆时针方向在六条射线上循环排列,周期为6。
计算 $2025 ÷ 6$,得商为337,余数为3。
因为余数为3,所以第2025个点与第3个点在同一条射线上。
由图可知,第3个点在射线OC上。
故第2025个点在射线OC上。
OC
计算 $2025 ÷ 6$,得商为337,余数为3。
因为余数为3,所以第2025个点与第3个点在同一条射线上。
由图可知,第3个点在射线OC上。
故第2025个点在射线OC上。
OC
11.(25分)如图,$AB// CD$,$EF$,$CG$分别是$∠AEC$,$∠ECD$的平分线。试说明:$EF// CG$。
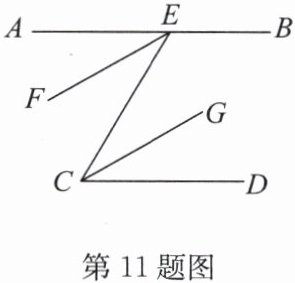

答案:解: 因为 $ AB // CD $ (已知),
所以 $ \angle AEC = \angle DCE $ (两直线平行, 内错角相等).
又因为 EF 平分 $ \angle AEC $ (已知),
所以 $ \angle FEC = \frac{1}{2} \angle AEC $ (角平分线的定义).
同理 $ \angle ECG = \frac{1}{2} \angle ECD $,
所以 $ \angle FEC = \angle ECG $ (等量代换),
所以 $ EF // CG $ (内错角相等, 两直线平行).
所以 $ \angle AEC = \angle DCE $ (两直线平行, 内错角相等).
又因为 EF 平分 $ \angle AEC $ (已知),
所以 $ \angle FEC = \frac{1}{2} \angle AEC $ (角平分线的定义).
同理 $ \angle ECG = \frac{1}{2} \angle ECD $,
所以 $ \angle FEC = \angle ECG $ (等量代换),
所以 $ EF // CG $ (内错角相等, 两直线平行).
12.(25分)如图,$∠MON = 140^{\circ}$,$∠AOC$与$∠BOC$互余,$OC$平分$∠MOB$。
(1)在图①中,若$∠AOC = 40^{\circ}$,则$∠BOC =$
(2)在图①中,设$∠AOC = \alpha$,$∠BON = \beta$,请探究$\alpha$与$\beta$之间的数量关系,并说明理由;
(3)在(2)中的条件不变的前提下,$∠AOB$绕着点$O$顺时针转动到如图②的位置,此时(2)中$\alpha$与$\beta$之间的数量关系是否还成立?请说明理由。

(1)在图①中,若$∠AOC = 40^{\circ}$,则$∠BOC =$
$50^{\circ}$
,$∠NOB =$$40^{\circ}$
;(2)在图①中,设$∠AOC = \alpha$,$∠BON = \beta$,请探究$\alpha$与$\beta$之间的数量关系,并说明理由;
(3)在(2)中的条件不变的前提下,$∠AOB$绕着点$O$顺时针转动到如图②的位置,此时(2)中$\alpha$与$\beta$之间的数量关系是否还成立?请说明理由。

(2)解: $ \beta = 2\alpha - 40^{\circ} $, 理由如下:
因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
又因为 $ \angle MON = \angle BOM + \angle BON $, $ \angle BON = \beta $,
所以 $ 140^{\circ} = 180^{\circ} - 2\alpha + \beta $, 即 $ \beta = 2\alpha - 40^{\circ} $.
(3)解: 不成立, 此时 $ \alpha $ 与 $ \beta $ 之间的数量关系为 $ 2\alpha + \beta = 40^{\circ} $.
理由: 因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
因为 $ \angle BOM = \angle MON + \angle BON $, $ \angle BON = \beta $,
所以 $ 180^{\circ} - 2\alpha = 140^{\circ} + \beta $, 即 $ 2\alpha + \beta = 40^{\circ} $.
因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
又因为 $ \angle MON = \angle BOM + \angle BON $, $ \angle BON = \beta $,
所以 $ 140^{\circ} = 180^{\circ} - 2\alpha + \beta $, 即 $ \beta = 2\alpha - 40^{\circ} $.
(3)解: 不成立, 此时 $ \alpha $ 与 $ \beta $ 之间的数量关系为 $ 2\alpha + \beta = 40^{\circ} $.
理由: 因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
因为 $ \angle BOM = \angle MON + \angle BON $, $ \angle BON = \beta $,
所以 $ 180^{\circ} - 2\alpha = 140^{\circ} + \beta $, 即 $ 2\alpha + \beta = 40^{\circ} $.
答案:(1) $ 50^{\circ} $ $ 40^{\circ} $
(2) 解: $ \beta = 2\alpha - 40^{\circ} $, 理由如下:
因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
又因为 $ \angle MON = \angle BOM + \angle BON $, $ \angle BON = \beta $,
所以 $ 140^{\circ} = 180^{\circ} - 2\alpha + \beta $, 即 $ \beta = 2\alpha - 40^{\circ} $.
(3) 解: 不成立, 此时 $ \alpha $ 与 $ \beta $ 之间的数量关系为 $ 2\alpha + \beta = 40^{\circ} $.
理由: 因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
因为 $ \angle BOM = \angle MON + \angle BON $, $ \angle BON = \beta $,
所以 $ 180^{\circ} - 2\alpha = 140^{\circ} + \beta $, 即 $ 2\alpha + \beta = 40^{\circ} $.
(2) 解: $ \beta = 2\alpha - 40^{\circ} $, 理由如下:
因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
又因为 $ \angle MON = \angle BOM + \angle BON $, $ \angle BON = \beta $,
所以 $ 140^{\circ} = 180^{\circ} - 2\alpha + \beta $, 即 $ \beta = 2\alpha - 40^{\circ} $.
(3) 解: 不成立, 此时 $ \alpha $ 与 $ \beta $ 之间的数量关系为 $ 2\alpha + \beta = 40^{\circ} $.
理由: 因为 $ \angle AOC = \alpha $, $ \angle AOC $ 与 $ \angle BOC $ 互余,
所以 $ \angle BOC = 90^{\circ} - \alpha $.
因为 OC 平分 $ \angle MOB $,
所以 $ \angle MOB = 2 \angle BOC = 2(90^{\circ} - \alpha) = 180^{\circ} - 2\alpha $.
因为 $ \angle BOM = \angle MON + \angle BON $, $ \angle BON = \beta $,
所以 $ 180^{\circ} - 2\alpha = 140^{\circ} + \beta $, 即 $ 2\alpha + \beta = 40^{\circ} $.