1. 某市冬季中的一天,中午12时的气温是$-3^{\circ }C$,经过6小时气温下降了$7^{\circ }C$,那么当天18时的气温是(
A.$10^{\circ }C$
B.$-10^{\circ }C$
C.$4^{\circ }C$
D.$-4^{\circ }C$
B
)A.$10^{\circ }C$
B.$-10^{\circ }C$
C.$4^{\circ }C$
D.$-4^{\circ }C$
答案:B
解析:
解:中午12时气温为$-3^{\circ}C$,经过6小时下降$7^{\circ}C$,则18时气温为$-3 - 7 = -10^{\circ}C$。
答案:B
答案:B
2. 下列运算正确的是(
A.$-2+(-5)= -(5-2)= -3$
B.$(+3)+(-8)= -(8-3)= -5$
C.$(-9)-(-2)= -(9+2)= -11$
D.$(+6)+(-4)= +(6+4)= +10$
B
)A.$-2+(-5)= -(5-2)= -3$
B.$(+3)+(-8)= -(8-3)= -5$
C.$(-9)-(-2)= -(9+2)= -11$
D.$(+6)+(-4)= +(6+4)= +10$
答案:B
解析:
解:
A. $-2+(-5)=-(2+5)=-7$,故A错误;
B. $(+3)+(-8)=-(8-3)=-5$,故B正确;
C. $(-9)-(-2)=-9+2=-7$,故C错误;
D. $(+6)+(-4)=+(6-4)=+2$,故D错误。
答案:B
A. $-2+(-5)=-(2+5)=-7$,故A错误;
B. $(+3)+(-8)=-(8-3)=-5$,故B正确;
C. $(-9)-(-2)=-9+2=-7$,故C错误;
D. $(+6)+(-4)=+(6-4)=+2$,故D错误。
答案:B
3. 将式子$(-20)+(+3)-(-5)-(+7)$省略括号和加号后变形正确的是(
A.$20-3+5-7$
B.$-20-3+5+7$
C.$-20+3+5-7$
D.$-20-3+5-7$
C
)A.$20-3+5-7$
B.$-20-3+5+7$
C.$-20+3+5-7$
D.$-20-3+5-7$
答案:C
解析:
解:$(-20)+(+3)-(-5)-(+7)$
$=-20+3+5-7$
结论:C
$=-20+3+5-7$
结论:C
4. 若两个数的和为负数,则这两个数(
A.都是负数
B.都是正数
C.至少有一个是负数
D.恰好一正一负
C
)A.都是负数
B.都是正数
C.至少有一个是负数
D.恰好一正一负
答案:C
解析:
解:分析各选项:
选项A:两个数都是负数时,和为负数,但并非唯一情况,例如-3+1=-2,和为负数但不都是负数,故A错误。
选项B:两个正数的和一定是正数,不可能为负数,故B错误。
选项C:若两个数的和为负数,假设两个数都不是负数(即都是非负数),则它们的和是非负数,与和为负数矛盾,所以至少有一个是负数,故C正确。
选项D:一正一负时和可能为负数,但两个负数的和也为负数,故D错误。
答案:C
选项A:两个数都是负数时,和为负数,但并非唯一情况,例如-3+1=-2,和为负数但不都是负数,故A错误。
选项B:两个正数的和一定是正数,不可能为负数,故B错误。
选项C:若两个数的和为负数,假设两个数都不是负数(即都是非负数),则它们的和是非负数,与和为负数矛盾,所以至少有一个是负数,故C正确。
选项D:一正一负时和可能为负数,但两个负数的和也为负数,故D错误。
答案:C
5. 若有理数$a$,$b$在数轴上的位置如图所示,则下列各式不成立的是(
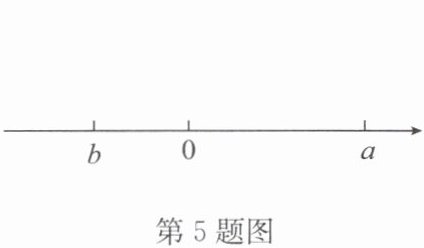
A.$a>-b$
B.$b-a<0$
C.$a>b$
D.$a+b<0$
D
)
A.$a>-b$
B.$b-a<0$
C.$a>b$
D.$a+b<0$
答案:D
解析:
由数轴可知:$b < 0 < a$,且$|a| > |b|$。
A. 因为$|a| > |b|$,$b < 0$,所以$-b > 0$,且$a > -b$,成立。
B. 因为$b < a$,所以$b - a < 0$,成立。
C. 因为$a$在$0$右侧,$b$在$0$左侧,所以$a > b$,成立。
D. 因为$|a| > |b|$,$a > 0$,$b < 0$,所以$a + b > 0$,不成立。
答案:D
A. 因为$|a| > |b|$,$b < 0$,所以$-b > 0$,且$a > -b$,成立。
B. 因为$b < a$,所以$b - a < 0$,成立。
C. 因为$a$在$0$右侧,$b$在$0$左侧,所以$a > b$,成立。
D. 因为$|a| > |b|$,$a > 0$,$b < 0$,所以$a + b > 0$,不成立。
答案:D
6. 计算:(1)$-180+90= $
$-90$
;(2)$-26-(-15)= $$-11$
;(3)$-3-6= $$-9$
.答案:6. (1) $-90$ (2) $-11$ (3) $-9$
解析:
(1) $-180 + 90 = -90$
(2) $-26 - (-15) = -26 + 15 = -11$
(3) $-3 - 6 = -9$
(2) $-26 - (-15) = -26 + 15 = -11$
(3) $-3 - 6 = -9$
7. 计算:
(1)$(-4)+(-7)= $
(4)$(+3.8)+(-4.9)= $
(1)$(-4)+(-7)= $
$-11$
;(2)$1.3+(-2.7)= $$-1.4$
;(3)$67+(-73)= $$-6$
;(4)$(+3.8)+(-4.9)= $
$-1.1$
;(5)$-6-9= $$-15$
;(6)$(-3)-(-11)= $$8$
.答案:7. (1) $-11$ (2) $-1.4$ (3) $-6$ (4) $-1.1$ (5) $-15$ (6) $8$
解析:
(1) $(-4)+(-7)=-11$;
(2) $1.3+(-2.7)=-1.4$;
(3) $67+(-73)=-6$;
(4) $(+3.8)+(-4.9)=-1.1$;
(5) $-6-9=-15$;
(6) $(-3)-(-11)=8$.
(2) $1.3+(-2.7)=-1.4$;
(3) $67+(-73)=-6$;
(4) $(+3.8)+(-4.9)=-1.1$;
(5) $-6-9=-15$;
(6) $(-3)-(-11)=8$.
8. 已知$x$是有理数,且$|x-7|+|y+2|= 0$,则$x+y= $
5
.答案:8. $5$
解析:
解:因为$|x - 7| + |y + 2| = 0$,且绝对值具有非负性,所以$|x - 7| = 0$,$|y + 2| = 0$。
由$|x - 7| = 0$,得$x - 7 = 0$,解得$x = 7$。
由$|y + 2| = 0$,得$y + 2 = 0$,解得$y = -2$。
所以$x + y = 7 + (-2) = 5$。
5
由$|x - 7| = 0$,得$x - 7 = 0$,解得$x = 7$。
由$|y + 2| = 0$,得$y + 2 = 0$,解得$y = -2$。
所以$x + y = 7 + (-2) = 5$。
5
9. 绝对值不大于6的所有负整数的和为
$-21$
.答案:9. $-21$
解析:
绝对值不大于6的负整数有:-1,-2,-3,-4,-5,-6。
它们的和为:(-1)+(-2)+(-3)+(-4)+(-5)+(-6) = -21。
-21
它们的和为:(-1)+(-2)+(-3)+(-4)+(-5)+(-6) = -21。
-21
10. 把1~9这9个数填入$3×3$的方格中,使其任意一行、任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.如图是仅可以看到部分数值的“九宫格”,则$x-y$的值为
$-3$
.答案:10. $-3$
解析:
解:在九宫格中,设中心数为5,幻和为 $ S $。
因为九宫格幻和 $ S = 3×5 = 15 $。
第一列:$ x + a + 8 = 15 $,得 $ a = 7 - x $(设第一列中间数为 $ a $)。
第二行:$ a + 5 + y = 15 $,将 $ a = 7 - x $ 代入,得 $ 7 - x + 5 + y = 15 $,即 $ -x + y = 3 $,所以 $ x - y = -3 $。
答案:$-3$
因为九宫格幻和 $ S = 3×5 = 15 $。
第一列:$ x + a + 8 = 15 $,得 $ a = 7 - x $(设第一列中间数为 $ a $)。
第二行:$ a + 5 + y = 15 $,将 $ a = 7 - x $ 代入,得 $ 7 - x + 5 + y = 15 $,即 $ -x + y = 3 $,所以 $ x - y = -3 $。
答案:$-3$
11. 如图,从左到右,在每个小格子中都填入一个整数,使其中任意三个相邻格子中所填整数之和都相等,则$c=$
3
,第200个格子中的数为-1
.答案:11. $3$ $-1$
解析:
由题意得:
因为任意三个相邻格子中所填整数之和都相等,所以$3 + a + b = a + b + c$,解得$c = 3$;
又因为$a + b + c = b + c + (-1)$,将$c = 3$代入得$a + b + 3 = b + 3 + (-1)$,解得$a=-1$;
再由$b + c + (-1) = c + (-1) + d$(设$c$右边的数为$d$),可得$b = d$,同理可推出这列数是以$3$,$-1$,$3$,$-1$,$\cdots$循环的,周期为$2$;
因为$200÷2 = 100$,所以第$200$个格子中的数为$-1$。
$c = 3$,第$200$个格子中的数为$-1$。
因为任意三个相邻格子中所填整数之和都相等,所以$3 + a + b = a + b + c$,解得$c = 3$;
又因为$a + b + c = b + c + (-1)$,将$c = 3$代入得$a + b + 3 = b + 3 + (-1)$,解得$a=-1$;
再由$b + c + (-1) = c + (-1) + d$(设$c$右边的数为$d$),可得$b = d$,同理可推出这列数是以$3$,$-1$,$3$,$-1$,$\cdots$循环的,周期为$2$;
因为$200÷2 = 100$,所以第$200$个格子中的数为$-1$。
$c = 3$,第$200$个格子中的数为$-1$。
12. 计算:
(1)$(-5)+(-2)+(+9)-(-8)$;
(2)$-4.27+3.8-0.73+1.2$;
(3)$8+(-11)-|-5|$;
(4)$(-\frac {1}{2})+(-\frac {7}{9})+(+1\frac {7}{9})$;
(5)$-\frac {1}{3}+\frac {1}{4}-\frac {1}{6}-\frac {1}{4}$;
(6)$1\frac {2}{3}+(-\frac {4}{5})-(+\frac {1}{5})+\frac {1}{3}$;
(7)$(+1.5)+(-\frac {1}{2})+(-\frac {3}{4})+(+1\frac {3}{4})$;
(8)$0.125+3\frac {1}{4}-\frac {1}{8}+5\frac {2}{3}-0.25$.
(1)$(-5)+(-2)+(+9)-(-8)$;
(2)$-4.27+3.8-0.73+1.2$;
(3)$8+(-11)-|-5|$;
(4)$(-\frac {1}{2})+(-\frac {7}{9})+(+1\frac {7}{9})$;
(5)$-\frac {1}{3}+\frac {1}{4}-\frac {1}{6}-\frac {1}{4}$;
(6)$1\frac {2}{3}+(-\frac {4}{5})-(+\frac {1}{5})+\frac {1}{3}$;
(7)$(+1.5)+(-\frac {1}{2})+(-\frac {3}{4})+(+1\frac {3}{4})$;
(8)$0.125+3\frac {1}{4}-\frac {1}{8}+5\frac {2}{3}-0.25$.
答案:12. 解:(1) 原式 $= (-5 - 2) + (9 + 8) = -7 + 17 = 10$。(2) 原式 $= (-4.27 - 0.73) + (3.8 + 1.2) = -5 + 5 = 0$。(3) 原式 $= 8 - 11 - 5 = -3 - 5 = -8$。(4) 原式 $= (-\frac{1}{2}) + (1\frac{7}{9} - \frac{7}{9}) = (-\frac{1}{2}) + 1 = \frac{1}{2}$。(5) 原式 $= -\frac{1}{3} - \frac{1}{6} = -\frac{1}{2}$。(6) 原式 $= (1\frac{2}{3} + \frac{1}{3}) - (\frac{4}{5} + \frac{1}{5}) = 2 - 1 = 1$。(7) 原式 $= (1.5 - \frac{1}{2}) + (1\frac{3}{4} - \frac{3}{4}) = 1 + 1 = 2$。(8) 原式 $= 0.125 + 3.25 - 0.125 + 5\frac{2}{3} - 0.25 = 0.125 - 0.125 + 3.25 - 0.25 + 5\frac{2}{3} = 3 + 5\frac{2}{3} = 8\frac{2}{3}$。