9. $1.89$亿可用科学记数法表示为
1.89×10⁸
。答案:1.89×10⁸
10. 数轴上与表示$-2$的点相距8个单位长度的点所表示的数为
6或−10
。答案:6或−10
解析:
解:当点在表示$-2$的点右侧时,该数为$-2 + 8 = 6$;
当点在表示$-2$的点左侧时,该数为$-2 - 8 = -10$。
故答案为:6或$-10$。
当点在表示$-2$的点左侧时,该数为$-2 - 8 = -10$。
故答案为:6或$-10$。
11. 单项式$-\frac{2}{5}a^{2}b$的系数是
−$\frac{2}{5}$
,次数是3
。答案:−$\frac{2}{5}$ 3
解析:
$-\frac{2}{5}$;3
12. 如图,在灯塔$O处观测到轮船M位于北偏西54^{\circ}12'36''$的方向,同时轮船$N在北偏东16.12^{\circ}$的方向,那么$\angle MON$的大小为
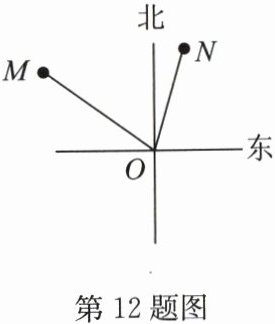
70.33
$^{\circ}$。
答案:70.33
解析:
解:将$54^{\circ}12'36''$转化为度:
$36'' = 36÷60 = 0.6'$,$12.6' = 12.6÷60 = 0.21^{\circ}$,所以$54^{\circ}12'36'' = 54.21^{\circ}$
$\angle MON = 54.21^{\circ} + 16.12^{\circ} = 70.33^{\circ}$
70.33
$36'' = 36÷60 = 0.6'$,$12.6' = 12.6÷60 = 0.21^{\circ}$,所以$54^{\circ}12'36'' = 54.21^{\circ}$
$\angle MON = 54.21^{\circ} + 16.12^{\circ} = 70.33^{\circ}$
70.33
13. 某商品如果按原售价的八折出售,将盈利10元;如果按原售价的六折出售,将亏损50元。设该商品的原售价为$x$元,则列方程为
0.8x−10=0.6x+50
。答案:0.8x−10=0.6x+50
解析:
解:设该商品的原售价为$x$元,商品的成本价是固定的。
按原售价的八折出售,售价为$0.8x$元,此时盈利10元,所以成本价为$0.8x - 10$元;
按原售价的六折出售,售价为$0.6x$元,此时亏损50元,所以成本价为$0.6x + 50$元。
因为成本价不变,所以可列方程为$0.8x - 10 = 0.6x + 50$。
$0.8x - 10 = 0.6x + 50$
按原售价的八折出售,售价为$0.8x$元,此时盈利10元,所以成本价为$0.8x - 10$元;
按原售价的六折出售,售价为$0.6x$元,此时亏损50元,所以成本价为$0.6x + 50$元。
因为成本价不变,所以可列方程为$0.8x - 10 = 0.6x + 50$。
$0.8x - 10 = 0.6x + 50$
14. 如图,由内角分别相等的四边形、五边形、六边形组合而成的图形中,若$\angle3= 60^{\circ}$,则$\angle1+\angle2$的度数为

72
度。
答案:72
15. 已知有理数$a$,$b$在数轴上的位置如图所示,且$|a|= |b|$,则关于$x的方程2025(a+b)-\frac{2a}{b}x= 5的解为x= $
$\frac{5}{2}$
。答案:$\frac{5}{2}$
解析:
解:由数轴知,$a<0$,$b>0$,又$|a|=|b|$,则$a=-b$,即$a+b=0$,$\frac{a}{b}=-1$。
将$a+b=0$,$\frac{a}{b}=-1$代入方程$2025(a+b)-\frac{2a}{b}x=5$,得:
$2025×0 - 2×(-1)\cdot x=5$
$2x=5$
$x=\frac{5}{2}$
答案:$\frac{5}{2}$
将$a+b=0$,$\frac{a}{b}=-1$代入方程$2025(a+b)-\frac{2a}{b}x=5$,得:
$2025×0 - 2×(-1)\cdot x=5$
$2x=5$
$x=\frac{5}{2}$
答案:$\frac{5}{2}$
16. 如图,在长方形$ABCD$中,$AB= 4$厘米,$BC= 6$厘米,点$E在边BC上且BE= 2EC$,动点$P从点A$出发,先以每秒1厘米的速度沿$A\to B$运动,然后以每秒2厘米的速度沿$B\to C$运动,再以每秒1厘米的速度沿$C\to D$运动,最终到达点$D$。设点$P运动的时间是t$秒,那么当$t= $

$\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$
时,三角形$APE$的面积等于5平方厘米。
答案:$\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$
解析:
解:在长方形$ABCD$中,$AB=4$厘米,$BC=6$厘米,$BE=2EC$,则$BE=4$厘米,$EC=2$厘米。
情况1:点$P$在$AB$上运动($0\leq t\leq4$)
此时$AP=t$厘米,$BP=(4-t)$厘米。
$S_{\triangle APE}=\frac{1}{2}× AP× BE=\frac{1}{2}× t×4=2t$
令$2t=5$,解得$t=\frac{5}{2}$。
情况2:点$P$在$BC$上运动($4< t\leq7$)
$AB$段用时4秒,$BP=2(t-4)$厘米,$PE=|BE-BP|=|4-2(t-4)|=|12-2t|$厘米。
$S_{\triangle APE}=\frac{1}{2}× AB× PE=\frac{1}{2}×4×|12-2t|=2|12-2t|$
令$2|12-2t|=5$,解得$t=\frac{19}{4}$($t=\frac{29}{4}$舍去,超出范围)。
情况3:点$P$在$CD$上运动($7< t\leq11$)
$AB+BC$段用时7秒,$CP=t-7$厘米,$DP=4-(t-7)=11-t$厘米。
$S_{\triangle APE}=S_{长方形ABCD}-S_{\triangle ABP}-S_{\triangle PCE}-S_{\triangle ADE}$
$=4×6-\frac{1}{2}×4×6-\frac{1}{2}×2×(t-7)-\frac{1}{2}×4×4$
$=24-12-(t-7)-8=11-t$
令$11-t=5$,解得$t=\frac{15}{2}$。
综上,$t=\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$。
答案:$\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$
情况1:点$P$在$AB$上运动($0\leq t\leq4$)
此时$AP=t$厘米,$BP=(4-t)$厘米。
$S_{\triangle APE}=\frac{1}{2}× AP× BE=\frac{1}{2}× t×4=2t$
令$2t=5$,解得$t=\frac{5}{2}$。
情况2:点$P$在$BC$上运动($4< t\leq7$)
$AB$段用时4秒,$BP=2(t-4)$厘米,$PE=|BE-BP|=|4-2(t-4)|=|12-2t|$厘米。
$S_{\triangle APE}=\frac{1}{2}× AB× PE=\frac{1}{2}×4×|12-2t|=2|12-2t|$
令$2|12-2t|=5$,解得$t=\frac{19}{4}$($t=\frac{29}{4}$舍去,超出范围)。
情况3:点$P$在$CD$上运动($7< t\leq11$)
$AB+BC$段用时7秒,$CP=t-7$厘米,$DP=4-(t-7)=11-t$厘米。
$S_{\triangle APE}=S_{长方形ABCD}-S_{\triangle ABP}-S_{\triangle PCE}-S_{\triangle ADE}$
$=4×6-\frac{1}{2}×4×6-\frac{1}{2}×2×(t-7)-\frac{1}{2}×4×4$
$=24-12-(t-7)-8=11-t$
令$11-t=5$,解得$t=\frac{15}{2}$。
综上,$t=\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$。
答案:$\frac{5}{2}$或$\frac{19}{4}$或$\frac{15}{2}$
17. (6分)计算:
(1)$(-9\frac{35}{36})×18$;
(2)$-1^{4}-\frac{1}{3}×[1-(-2)^{3}]-|\pi-4|$。
(1)$(-9\frac{35}{36})×18$;
(2)$-1^{4}-\frac{1}{3}×[1-(-2)^{3}]-|\pi-4|$。
答案:解:(1)原式=(−10+$\frac{1}{36}$)×18=−10×18+$\frac{1}{36}$×18=−180+$\frac{1}{2}$=−179$\frac{1}{2}$.
(2)原式=−1−$\frac{1}{3}$×[1−(−8)]+π−4=−1−3+π−4=π−8.
(2)原式=−1−$\frac{1}{3}$×[1−(−8)]+π−4=−1−3+π−4=π−8.
18. (6分)解方程:
(1)$x+1= 3(x-1)$;
(2)$\frac{x-3}{2}-1= \frac{4x+1}{5}$。
(1)$x+1= 3(x-1)$;
(2)$\frac{x-3}{2}-1= \frac{4x+1}{5}$。
答案:解:(1)去括号,得x+1=3x−3,
移项、合并同类项,得2x=4,
系数化为1,得x=2.
(2)去分母,得5(x−3)−10=2(4x+1),
去括号,得5x−15−10=8x+2,
移项、合并同类项,得−3x=27,
系数化为1,得x=−9.
移项、合并同类项,得2x=4,
系数化为1,得x=2.
(2)去分母,得5(x−3)−10=2(4x+1),
去括号,得5x−15−10=8x+2,
移项、合并同类项,得−3x=27,
系数化为1,得x=−9.