19. (8分)(2024·靖江月考)先化简,再求值:$6y^{2}-(2x^{2}-y)+2(x^{2}-3y^{2})$,其中$x= -2024$,$y= 2025$。
答案:解:原式=6y²−2x²+y+2x²−6y²=y,
当y=2025时,原式=2025.
当y=2025时,原式=2025.
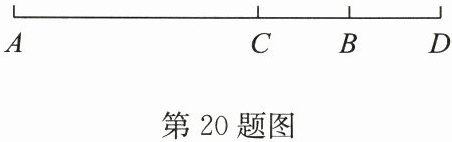
20. (6分)如图,$C为线段AD$上一点,$B为线段CD$的中点,且$AD= 14$厘米,$BD= 3$厘米。
(1)图中共有几条线段;
(2)求$AC$的长。
(1)图中共有几条线段;
(2)求$AC$的长。

答案:解:(1)共有6条线段,分别是线段AC,线段AB,线段AD,线段BC,线段CD,线段BD.
(2)因为B为线段CD的中点,
所以CD=2BD=2×3=6(厘米),
所以AC=AD−CD=14−6=8(厘米).
(2)因为B为线段CD的中点,
所以CD=2BD=2×3=6(厘米),
所以AC=AD−CD=14−6=8(厘米).
21. (6分)如图,直线$AB与CD相交于点O$,$OE\perp AB$,$OF\perp CD$。
(1)图中与$\angle COE$互补的角是______
(2)若$\angle AOD= \frac{1}{5}\angle EOF$,求$\angle AOD$的度数。

(2)解:设∠AOD=x,则∠EOF=5x,∠EOC=90°−x.因为∠AOD=∠BOC,
所以∠EOF=∠EOC+∠COF=90°−x+90°=5x,
解得x=30°.
所以∠AOD=30°.
(1)图中与$\angle COE$互补的角是______
∠EOD,∠AOF
;(把符合条件的角都写出来)(2)若$\angle AOD= \frac{1}{5}\angle EOF$,求$\angle AOD$的度数。

(2)解:设∠AOD=x,则∠EOF=5x,∠EOC=90°−x.因为∠AOD=∠BOC,
所以∠EOF=∠EOC+∠COF=90°−x+90°=5x,
解得x=30°.
所以∠AOD=30°.
答案:(1)∠EOD,∠AOF
(2)解:设∠AOD=x,则∠EOF=5x,∠EOC=90°−x.因为∠AOD=∠BOC,
所以∠EOF=∠EOC+∠COF=90°−x+90°=5x,
解得x=30°.
所以∠AOD=30°.
(2)解:设∠AOD=x,则∠EOF=5x,∠EOC=90°−x.因为∠AOD=∠BOC,
所以∠EOF=∠EOC+∠COF=90°−x+90°=5x,
解得x=30°.
所以∠AOD=30°.
22. (6分)已知$A= 5x^{2}-mx+n$,$B= -3y^{2}+2x-1$,$m$,$n$为常数,若$A+B$中不含一次项和常数项,求$2(m^{2}n-1)-5m^{2}n+4$的值。
答案:解:因为A=5x²−mx+n,B=−3y²+2x−1,
所以A+B=(5x²−mx+n)+(−3y²+2x−1)=5x²−mx+n−3y²+2x−1=5x²−3y²+(2−m)x+(n−1).
因为A+B中不含一次项和常数项,
所以2−m=0,n−1=0,
解得m=2,n=1.
所以2(m²n−1)−5m²n+4=2m²n−2−5m²n+4=−3m²n+2=−3×2²×1+2=−12+2=−10.
所以A+B=(5x²−mx+n)+(−3y²+2x−1)=5x²−mx+n−3y²+2x−1=5x²−3y²+(2−m)x+(n−1).
因为A+B中不含一次项和常数项,
所以2−m=0,n−1=0,
解得m=2,n=1.
所以2(m²n−1)−5m²n+4=2m²n−2−5m²n+4=−3m²n+2=−3×2²×1+2=−12+2=−10.
23. (6分)如图,线段$AB= 12cm$,延长$AB到点C$,使$BC= 8cm$,$M$,$N分别为线段AC$,$BC$的中点,求线段$MN$的长。


答案:解:因为AB=12cm,BC=8cm,
所以AC=AB+BC=12+8=20(cm).
因为M,N分别为线段AC,BC的中点,
所以CM=$\frac{1}{2}$AC=10cm,CN=$\frac{1}{2}$BC=4cm,
所以MN=CM−CN=10−4=6(cm).
所以AC=AB+BC=12+8=20(cm).
因为M,N分别为线段AC,BC的中点,
所以CM=$\frac{1}{2}$AC=10cm,CN=$\frac{1}{2}$BC=4cm,
所以MN=CM−CN=10−4=6(cm).