24. (8分)新定义:如果两个一元一次方程的解互为相反数,就称这两个方程为“友好方程”,例如,方程$2x= 6和3x+9= 0$为“友好方程”。
(1)若关于$x的方程3x+m= 0与方程2x-6= 4$是“友好方程”,求$m$的值;
(2)若某“友好方程”的两个解的差为6,其中一个解为$n$,求$n$的值。
(1)若关于$x的方程3x+m= 0与方程2x-6= 4$是“友好方程”,求$m$的值;
(2)若某“友好方程”的两个解的差为6,其中一个解为$n$,求$n$的值。
答案:解:(1)方程2x−6=4的解为x=5.
因为关于x的方程3x+m=0与方程2x−6=4是“友好方程”,
所以关于x的方程3x+m=0的解为x=−5,所以3×(−5)+m=0,解得m=15.
(2)因为某“友好方程”的一个解为n,
所以另一个解为−n,
所以n−(−n)=6或−n−n=6,
解得n=3或n=−3.
因为关于x的方程3x+m=0与方程2x−6=4是“友好方程”,
所以关于x的方程3x+m=0的解为x=−5,所以3×(−5)+m=0,解得m=15.
(2)因为某“友好方程”的一个解为n,
所以另一个解为−n,
所以n−(−n)=6或−n−n=6,
解得n=3或n=−3.
25. (8分)在某城市美化工程招标时,有甲、乙两个工程队投标。经测算,甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合作完成。
(1)甲、乙两队需合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元。若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
(1)甲、乙两队需合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元。若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
答案:解:(1)设甲、乙两队需合作t天,
根据题意,得$\frac{t+20}{60}$+$\frac{t}{90}$=1,解得t=24.
答:甲、乙两队需合作24天.
(2)设甲、乙合作完成需y天,则有($\frac{1}{60}$+$\frac{1}{90}$)×y=1,解得y=36.
①甲队单独完成需付工程款60×3.5=210(万元);
②乙队单独完成超过计划天数,不符合题意;
③甲、乙两队合作完成需付工程款36×(3.5+2)=198(万元).
因为210>198,
所以由甲、乙两队全程合作完成该工程省钱.
答:在不超过计划天数的前提下,由甲、乙两队全程合作完成该工程省钱.
根据题意,得$\frac{t+20}{60}$+$\frac{t}{90}$=1,解得t=24.
答:甲、乙两队需合作24天.
(2)设甲、乙合作完成需y天,则有($\frac{1}{60}$+$\frac{1}{90}$)×y=1,解得y=36.
①甲队单独完成需付工程款60×3.5=210(万元);
②乙队单独完成超过计划天数,不符合题意;
③甲、乙两队合作完成需付工程款36×(3.5+2)=198(万元).
因为210>198,
所以由甲、乙两队全程合作完成该工程省钱.
答:在不超过计划天数的前提下,由甲、乙两队全程合作完成该工程省钱.
26. (10分)如图,$P是线段AB$上任意一点,$AB= 12cm$,$C$,$D两点分别从点P$,$B同时出发向点A$运动,且点$C的运动速度为2cm/s$,点$D的运动速度为3cm/s$,运动的时间为$t\ s$。
(1)若$AP= 8cm$。
①运动$1s$后,求$CD$的长;
②当点$D在线段PB$上运动时,试说明$AC= 2CD$。
(2)如果当$t= 2$时,$CD= 1cm$,试探索$AP$的长。

(1)若$AP= 8cm$。
①运动$1s$后,求$CD$的长;
②当点$D在线段PB$上运动时,试说明$AC= 2CD$。
(2)如果当$t= 2$时,$CD= 1cm$,试探索$AP$的长。

答案:
解:(1)①由题意,得CP=2×1=2(cm),DB=3×1=3(cm).
因为AP=8cm,AB=12cm,所以PB=AB−AP=4cm,所以CD=CP+PB−DB=2+4−3=3(cm).
②因为AC=(8−2t)cm,DP=(4−3t)cm,
所以CD=DP+CP=4−3t+2t=(4−t)cm,
所以AC=2CD.
(2)当t=2时,CP=2×2=4(cm),DB=3×2=6(cm),当点D在点C的右边时,如答图①.

因为CD=1cm,所以CB=CD+DB=1+6=7(cm),所以AC=AB−CB=12−7=5(cm),所以AP=AC+CP=5+4=9(cm).
当点D在点C的左边时,如答图②.
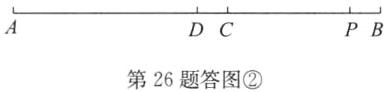
因为AD=AB−DB=12−6=6(cm),
所以AP=AD+CD+CP=6+1+4=11(cm).
综上所述,AP的长为9cm或11cm.
解:(1)①由题意,得CP=2×1=2(cm),DB=3×1=3(cm).
因为AP=8cm,AB=12cm,所以PB=AB−AP=4cm,所以CD=CP+PB−DB=2+4−3=3(cm).
②因为AC=(8−2t)cm,DP=(4−3t)cm,
所以CD=DP+CP=4−3t+2t=(4−t)cm,
所以AC=2CD.
(2)当t=2时,CP=2×2=4(cm),DB=3×2=6(cm),当点D在点C的右边时,如答图①.

因为CD=1cm,所以CB=CD+DB=1+6=7(cm),所以AC=AB−CB=12−7=5(cm),所以AP=AC+CP=5+4=9(cm).
当点D在点C的左边时,如答图②.

因为AD=AB−DB=12−6=6(cm),
所以AP=AD+CD+CP=6+1+4=11(cm).
综上所述,AP的长为9cm或11cm.
27. (12分)如图①,将一副三角尺摆放在直线$MN$上,在三角尺$OAB和三角尺OCD$中,$\angle OAB= \angle OCD= 90^{\circ}$,$\angle AOB= 45^{\circ}$,$\angle COD= 30^{\circ}$。
(1)保持三角尺$OCD$不动,当三角尺$OAB$旋转至图②位置时,$\angle BOD与\angle AON$有怎样的数量关系?请说明理由。
(2)如图③,若三角尺$OAB开始绕点O$以每秒6度的速度逆时针旋转的同时,三角尺$OCD也绕点O$以每秒3度的速度逆时针旋转,当$OB旋转至射线OM$上时,两块三角尺同时停止转动。设旋转时间为$t$秒,则在此过程中,是否存在$t$,使得$\angle BOD+\angle AON= 60^{\circ}$?若存在,求出$t$的值;若不存在,请说明理由。

(1)保持三角尺$OCD$不动,当三角尺$OAB$旋转至图②位置时,$\angle BOD与\angle AON$有怎样的数量关系?请说明理由。
(2)如图③,若三角尺$OAB开始绕点O$以每秒6度的速度逆时针旋转的同时,三角尺$OCD也绕点O$以每秒3度的速度逆时针旋转,当$OB旋转至射线OM$上时,两块三角尺同时停止转动。设旋转时间为$t$秒,则在此过程中,是否存在$t$,使得$\angle BOD+\angle AON= 60^{\circ}$?若存在,求出$t$的值;若不存在,请说明理由。

答案:解:(1)∠BOD−∠AON=15°.理由如下:
由题意,得∠BOD=∠AOB+∠AOD=45°+∠AOD,∠AON=∠COD+∠AOD=30°+∠AOD,
所以∠BOD−∠AON=45°+∠AOD−(30°+∠AOD)=15°.
(2)存在.
由题意,得∠BON=(6t)°,∠DON=30°+(3t)°.
当OA与ON重合时,6t=45,解得t=$\frac{15}{2}$;
当OB与OD重合时,6t=30+3t,解得t=10;
当OB与OM重合时,6t=180,解得t=30.
①当0≤t≤$\frac{15}{2}$时,∠AON=45°−(6t)°,∠BOD=30°+(3t)°−(6t)°=30°−(3t)°,
则∠BOD+∠AON=75°−(9t)°=60°,
解得t=$\frac{5}{3}$;
②当$\frac{15}{2}$<t≤10时,∠AON=(6t)°−45°,∠BOD=30°+(3t)°−(6t)°=30°−(3t)°,
则∠BOD+∠AON=(3t)°−15°=60°,
解得t=25(不符合题意,舍去);
③当10<t≤30时,∠AON=(6t)°−45°,∠BOD=(6t)°−[30°+(3t)°]=(3t)°−30°,
则∠BOD+∠AON=(9t)°−75°=60°,
解得t=15.
综上所述,当t的值为$\frac{5}{3}$或15时,∠BOD+∠AON=60°.
由题意,得∠BOD=∠AOB+∠AOD=45°+∠AOD,∠AON=∠COD+∠AOD=30°+∠AOD,
所以∠BOD−∠AON=45°+∠AOD−(30°+∠AOD)=15°.
(2)存在.
由题意,得∠BON=(6t)°,∠DON=30°+(3t)°.
当OA与ON重合时,6t=45,解得t=$\frac{15}{2}$;
当OB与OD重合时,6t=30+3t,解得t=10;
当OB与OM重合时,6t=180,解得t=30.
①当0≤t≤$\frac{15}{2}$时,∠AON=45°−(6t)°,∠BOD=30°+(3t)°−(6t)°=30°−(3t)°,
则∠BOD+∠AON=75°−(9t)°=60°,
解得t=$\frac{5}{3}$;
②当$\frac{15}{2}$<t≤10时,∠AON=(6t)°−45°,∠BOD=30°+(3t)°−(6t)°=30°−(3t)°,
则∠BOD+∠AON=(3t)°−15°=60°,
解得t=25(不符合题意,舍去);
③当10<t≤30时,∠AON=(6t)°−45°,∠BOD=(6t)°−[30°+(3t)°]=(3t)°−30°,
则∠BOD+∠AON=(9t)°−75°=60°,
解得t=15.
综上所述,当t的值为$\frac{5}{3}$或15时,∠BOD+∠AON=60°.