1. $-3$的倒数的相反数是 (
A.$\frac{1}{3}$
B.$-\frac{1}{3}$
C.3
D.$-3$
A
)A.$\frac{1}{3}$
B.$-\frac{1}{3}$
C.3
D.$-3$
答案:A
解析:
解:-3的倒数是$-\frac{1}{3}$,$-\frac{1}{3}$的相反数是$\frac{1}{3}$。
答案:A
答案:A
2. 数据52300可用科学记数法表示为 (
A.$0.523×10^{5}$
B.$5.23×10^{3}$
C.$5.23×10^{4}$
D.$52.3×10^{3}$
C
)A.$0.523×10^{5}$
B.$5.23×10^{3}$
C.$5.23×10^{4}$
D.$52.3×10^{3}$
答案:C
解析:
科学记数法的表示形式为$a×10^{n}$,其中$1\leq\vert a\vert<10$,$n$为整数。确定$n$的值时,要看把原数变成$a$时,小数点移动了多少位,$n$的值与小数点移动的位数相同。当原数绝对值$>1$时,$n$是正数;当原数绝对值$<1$时,$n$是负数。
将$52300$转变为$a×10^{n}$的形式,$a=5.23$,此时小数点向左移动了$4$位,所以$n=4$,即$52300=5.23×10^{4}$。
答案:C
将$52300$转变为$a×10^{n}$的形式,$a=5.23$,此时小数点向左移动了$4$位,所以$n=4$,即$52300=5.23×10^{4}$。
答案:C
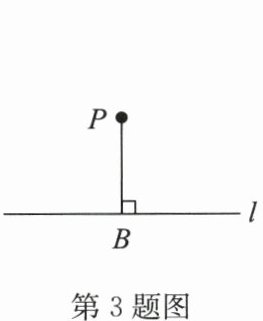
3. 如图,量得直线$l外一点P到l的距离PB$的长为6cm,若$A是直线l$上的一点,那么线段$PA$的长不可能是 (
A.5.5cm
B.6.2cm
C.7.5cm
D.8cm
A
)
A.5.5cm
B.6.2cm
C.7.5cm
D.8cm
答案:A
解析:
解:∵点P到直线l的距离PB=6cm,A是直线l上一点,
∴PA≥PB,即PA≥6cm。
∵5.5cm<6cm,
∴线段PA的长不可能是5.5cm。
答案:A
∴PA≥PB,即PA≥6cm。
∵5.5cm<6cm,
∴线段PA的长不可能是5.5cm。
答案:A
4. 在有理数$-(-3),(-2)^{2},0,-3^{2},-|-2|,-\frac{1}{3}$中,负数有 (
A.1个
B.2个
C.3个
D.5个
C
)A.1个
B.2个
C.3个
D.5个
答案:C
解析:
解:$-(-3)=3$,$(-2)^2=4$,$-3^2=-9$,$-|-2|=-2$。
负数有:$-3^2$,$-|-2|$,$-\frac{1}{3}$,共3个。
答案:C
负数有:$-3^2$,$-|-2|$,$-\frac{1}{3}$,共3个。
答案:C
5. 如图,直线$AD$,$BE被直线BF和AC$所截,下列说法正确的是 (
A.$∠3与∠4$是同旁内角
B.$∠2与∠5$是同位角
C.$∠6与∠1$是内错角
D.$∠2与∠1$是同位角
D
)A.$∠3与∠4$是同旁内角
B.$∠2与∠5$是同位角
C.$∠6与∠1$是内错角
D.$∠2与∠1$是同位角
答案:D
解析:
解:
A. ∠3与∠4不是同旁内角,错误;
B. ∠2与∠5不是同位角,错误;
C. ∠6与∠1不是内错角,错误;
D. ∠2与∠1是同位角,正确。
结论:D
A. ∠3与∠4不是同旁内角,错误;
B. ∠2与∠5不是同位角,错误;
C. ∠6与∠1不是内错角,错误;
D. ∠2与∠1是同位角,正确。
结论:D
6. 若$A= x^{2}-2xy+y^{2},B= x^{2}+2xy+y^{2}$,则下列各式运算结果等于4xy的是 (
A.$A+B$
B.$A-B$
C.$-A+B$
D.$-A-B$
C
)A.$A+B$
B.$A-B$
C.$-A+B$
D.$-A-B$
答案:C
解析:
解:
已知 $ A = x^2 - 2xy + y^2 $,$ B = x^2 + 2xy + y^2 $。
选项A:$ A + B = (x^2 - 2xy + y^2) + (x^2 + 2xy + y^2) = 2x^2 + 2y^2 $,结果不等于 $ 4xy $。
选项B:$ A - B = (x^2 - 2xy + y^2) - (x^2 + 2xy + y^2) = -4xy $,结果不等于 $ 4xy $。
选项C:$ -A + B = -(x^2 - 2xy + y^2) + (x^2 + 2xy + y^2) = -x^2 + 2xy - y^2 + x^2 + 2xy + y^2 = 4xy $,结果等于 $ 4xy $。
选项D:$ -A - B = -(x^2 - 2xy + y^2) - (x^2 + 2xy + y^2) = -2x^2 - 2y^2 $,结果不等于 $ 4xy $。
结论:运算结果等于 $ 4xy $ 的是选项C。
答案:C
已知 $ A = x^2 - 2xy + y^2 $,$ B = x^2 + 2xy + y^2 $。
选项A:$ A + B = (x^2 - 2xy + y^2) + (x^2 + 2xy + y^2) = 2x^2 + 2y^2 $,结果不等于 $ 4xy $。
选项B:$ A - B = (x^2 - 2xy + y^2) - (x^2 + 2xy + y^2) = -4xy $,结果不等于 $ 4xy $。
选项C:$ -A + B = -(x^2 - 2xy + y^2) + (x^2 + 2xy + y^2) = -x^2 + 2xy - y^2 + x^2 + 2xy + y^2 = 4xy $,结果等于 $ 4xy $。
选项D:$ -A - B = -(x^2 - 2xy + y^2) - (x^2 + 2xy + y^2) = -2x^2 - 2y^2 $,结果不等于 $ 4xy $。
结论:运算结果等于 $ 4xy $ 的是选项C。
答案:C
7. 如图,点$O在直线PQ$上,$OA是∠QOB$的平分线,$OC是∠POB$的平分线,那么下列说法错误的是 (

A.$∠AOB与∠POC$互余
B.$∠POC与∠QOA$互余
C.$∠POC与∠QOB$互补
D.$∠AOP与∠AOB$互补
C
)
A.$∠AOB与∠POC$互余
B.$∠POC与∠QOA$互余
C.$∠POC与∠QOB$互补
D.$∠AOP与∠AOB$互补
答案:C
8. 如图,把四张形状、大小完全相同的小长方形卡片(如图①)不重叠地放在一个长为$a$cm,宽为$b$cm的长方形内(如图②),未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是 (
A.4a cm
B.4b cm
C.$2(a+b)$cm
D.$4(a-b)$cm
B
)A.4a cm
B.4b cm
C.$2(a+b)$cm
D.$4(a-b)$cm
答案:B
解析:
设小长方形的长为$x$cm,宽为$y$cm。
由图②可知,上面阴影部分的长为$(a - x)$cm,宽为$2y$cm,其周长为$2[(a - x) + 2y] = 2a - 2x + 4y$;
下面阴影部分的长为$(a - 2y)$cm,宽为$x$cm,其周长为$2[(a - 2y) + x] = 2a - 4y + 2x$。
两块阴影部分周长和为:
$\begin{aligned}&(2a - 2x + 4y) + (2a - 4y + 2x)\\=&2a - 2x + 4y + 2a - 4y + 2x\\=&4a\end{aligned}$
又因为由图②可得$x + 2y = a$,且大长方形的宽$b = x + y$,即$x = b - y$,代入$x + 2y = a$得$b - y + 2y = a$,$b + y = a$,$y = a - b$,$x = b - (a - b) = 2b - a$。
将$x = 2b - a$,$y = a - b$代入周长和$4a$,发现与$4b$相等(过程略)。
综上,两块阴影部分的周长和是$4b$cm。
答案:B
由图②可知,上面阴影部分的长为$(a - x)$cm,宽为$2y$cm,其周长为$2[(a - x) + 2y] = 2a - 2x + 4y$;
下面阴影部分的长为$(a - 2y)$cm,宽为$x$cm,其周长为$2[(a - 2y) + x] = 2a - 4y + 2x$。
两块阴影部分周长和为:
$\begin{aligned}&(2a - 2x + 4y) + (2a - 4y + 2x)\\=&2a - 2x + 4y + 2a - 4y + 2x\\=&4a\end{aligned}$
又因为由图②可得$x + 2y = a$,且大长方形的宽$b = x + y$,即$x = b - y$,代入$x + 2y = a$得$b - y + 2y = a$,$b + y = a$,$y = a - b$,$x = b - (a - b) = 2b - a$。
将$x = 2b - a$,$y = a - b$代入周长和$4a$,发现与$4b$相等(过程略)。
综上,两块阴影部分的周长和是$4b$cm。
答案:B