24. (6分)如图,直线$AB$,$CD相交于点O$,将一块直角三角尺的直角顶点放置在点$O$处,且$ON平分∠BOD$.
(1)若$∠AOC = 64^{\circ}$,求$∠MOB$的度数;
(2)试说明:$OM平分∠AOD$.
(1)若$∠AOC = 64^{\circ}$,求$∠MOB$的度数;
(2)试说明:$OM平分∠AOD$.
答案：解: (1) 因为$∠AOC=64^{\circ },$所以$∠BOD=64^{\circ }.$因为 ON 平分$∠BOD,$所以$∠BON=32^{\circ },$所以$∠MOB=∠MON+∠BON=90^{\circ }+32^{\circ }=122^{\circ }.$ (2) 因为$∠MON=90^{\circ },$所以$∠MOD+∠NOD=∠AOM+∠BON=90^{\circ }.$因为$∠BON=∠DON,$所以$∠MOD=∠AOM$, 即 OM 平分$∠AOD.$
解析：
(1) 解：因为∠AOC=64°，
所以∠BOD=∠AOC=64°（对顶角相等）。
因为ON平分∠BOD，
所以∠BON=∠DON=∠BOD/2=64°/2=32°。
因为∠MON=90°（直角三角尺直角顶点在O处），
所以∠MOB=∠MON+∠BON=90°+32°=122°。
(2) 证明：因为∠MON=90°，
所以∠MOD+∠DON=90°。
因为∠AOB=180°（平角定义），
所以∠AOM+∠MON+∠BON=180°，
即∠AOM+90°+∠BON=180°，
所以∠AOM+∠BON=90°。
又因为ON平分∠BOD，
所以∠BON=∠DON，
所以∠MOD=∠AOM（等角的余角相等），
即OM平分∠AOD。
所以∠BOD=∠AOC=64°（对顶角相等）。
因为ON平分∠BOD，
所以∠BON=∠DON=∠BOD/2=64°/2=32°。
因为∠MON=90°（直角三角尺直角顶点在O处），
所以∠MOB=∠MON+∠BON=90°+32°=122°。
(2) 证明：因为∠MON=90°，
所以∠MOD+∠DON=90°。
因为∠AOB=180°（平角定义），
所以∠AOM+∠MON+∠BON=180°，
即∠AOM+90°+∠BON=180°，
所以∠AOM+∠BON=90°。
又因为ON平分∠BOD，
所以∠BON=∠DON，
所以∠MOD=∠AOM（等角的余角相等），
即OM平分∠AOD。
25. (8分)某商场需订购一批袜子,现有甲、乙两个供应商,均标价每双8元.为了促销,甲说:“凡来我店进货一律九折.”乙说:“如果超出60双,那么超出的部分打八折”.
(1)购进多少双时,去两个供应商处的进货价钱一样多?
(2)第一次购进了100双,第二次购进的数量比第一次的2倍多10双.如果你是商场的经理,请设计一种购买方案,使得两次总进货价最少,并计算出总进货价为多少元.
(1)购进多少双时,去两个供应商处的进货价钱一样多?
(2)第一次购进了100双,第二次购进的数量比第一次的2倍多10双.如果你是商场的经理,请设计一种购买方案,使得两次总进货价最少,并计算出总进货价为多少元.
答案：解: (1) 设购进 x 双时, 去两个供应商处的进货价钱一样多.根据题意, 得$8×0.9x=8×60+8×0.8(x-60),$解得$x=120.$答: 购进 120 双时, 去两个供应商处的进货价钱一样多. (2) 第一次选择甲供应商, 需要$8×0.9×100=720$(元),第二次选择乙供应商, 需要$8×60+8×0.8×(100×2+10-60)=1440$(元),$720+1440=2160$(元).答: 总进货价为 2160 元.
解析：
(1) 设购进 $ x $ 双时，去两个供应商处的进货价钱一样多。
根据题意，得 $ 8 × 0.9x = 8 × 60 + 8 × 0.8(x - 60) $，
解得 $ x = 120 $。
答：购进 120 双时，去两个供应商处的进货价钱一样多。
(2) 第一次购进 100 双：
选择甲供应商，费用为 $ 8 × 0.9 × 100 = 720 $ 元。
第二次购进数量为 $ 100 × 2 + 10 = 210 $ 双：
选择乙供应商，费用为 $ 8 × 60 + 8 × 0.8 × (210 - 60) = 1440 $ 元。
总进货价为 $ 720 + 1440 = 2160 $ 元。
答：总进货价为 2160 元。
根据题意，得 $ 8 × 0.9x = 8 × 60 + 8 × 0.8(x - 60) $，
解得 $ x = 120 $。
答：购进 120 双时，去两个供应商处的进货价钱一样多。
(2) 第一次购进 100 双：
选择甲供应商，费用为 $ 8 × 0.9 × 100 = 720 $ 元。
第二次购进数量为 $ 100 × 2 + 10 = 210 $ 双：
选择乙供应商，费用为 $ 8 × 60 + 8 × 0.8 × (210 - 60) = 1440 $ 元。
总进货价为 $ 720 + 1440 = 2160 $ 元。
答：总进货价为 2160 元。
26. (10分)如图,在一条不完整的数轴上从左到右有点$A$,$B$,$C$,其中$AB = 2$,$BC = 1$.
(1)若以$B$为原点,点$A$表示的数是______
(2)若$O$是数轴上的原点,且$A是线段OC$的中点,直接写出点$A$,$B$,$C$表示的数;
(3)若$O$是数轴上的原点,且$BO = 2025$,求点$A$,$B$,$C$表示的数.
(1)若以$B$为原点,点$A$表示的数是______
-2
,点$C$表示的数是______1
;(2)若$O$是数轴上的原点,且$A是线段OC$的中点,直接写出点$A$,$B$,$C$表示的数;
解: 因为$AB=2,BC=1,$所以$AC=AB+BC=3.$因为 A 是线段 OC 的中点,所以$CO=6,OA=AC=3,$所以$OB=OA+AB=5.$因为 O 是数轴上的原点,所以点 A 表示的数是 3, 点 B 表示的数是 5, 点 C 表示的数是 6.
(3)若$O$是数轴上的原点,且$BO = 2025$,求点$A$,$B$,$C$表示的数.
解: 当点 O 在点 B 的左侧时,因为$BO=2025,AB=2,BC=1,$所以$AO=OB-AB=2023,CO=OB+BC=2026,$所以点 A 表示的数是 2023, 点 B 表示的数是 2025, 点 C 表示的数是 2026;当点 O 在点 B 的右侧时,因为$BO=2025,AB=2,BC=1,$所以$AO=OB+AB=2027,CO=OB-BC=2024,$所以点 A 表示的数是 -2027, 点 B 表示的数是 -2025, 点 C 表示的数是 -2024.综上, 点 A, B, C 表示的数分别为 2023, 2025, 2026 或-2027, -2025, -2024.
答案：(1) -2 1 (2) 解: 因为$AB=2,BC=1,$所以$AC=AB+BC=3.$因为 A 是线段 OC 的中点,所以$CO=6,OA=AC=3,$所以$OB=OA+AB=5.$因为 O 是数轴上的原点,所以点 A 表示的数是 3, 点 B 表示的数是 5, 点 C 表示的数是 6. (3) 解: 当点 O 在点 B 的左侧时,因为$BO=2025,AB=2,BC=1,$所以$AO=OB-AB=2023,CO=OB+BC=2026,$所以点 A 表示的数是 2023, 点 B 表示的数是 2025, 点 C 表示的数是 2026;当点 O 在点 B 的右侧时,因为$BO=2025,AB=2,BC=1,$所以$AO=OB+AB=2027,CO=OB-BC=2024,$所以点 A 表示的数是 -2027, 点 B 表示的数是 -2025, 点 C 表示的数是 -2024.综上, 点 A, B, C 表示的数分别为 2023, 2025, 2026 或-2027, -2025, -2024.
解析：
(1) -2；1
(2) 解：因为$AB = 2$，$BC = 1$，所以$AC=AB + BC=3$。
因为$A$是线段$OC$的中点，所以$OA=AC = 3$，$OC=2OA = 6$。
所以$OB=OA+AB=3 + 2=5$。
因此，点$A$表示的数是$3$，点$B$表示的数是$5$，点$C$表示的数是$6$。
(3) 解：当点$O$在点$B$左侧时，
因为$BO = 2025$，$AB=2$，$BC = 1$，
所以点$B$表示的数是$2025$，
点$A$表示的数是$2025-2=2023$，
点$C$表示的数是$2025 + 1=2026$。
当点$O$在点$B$右侧时，
因为$BO = 2025$，$AB = 2$，$BC=1$，
所以点$B$表示的数是$-2025$，
点$A$表示的数是$-2025-2=-2027$，
点$C$表示的数是$-2025 + 1=-2024$。
综上，点$A$，$B$，$C$表示的数分别为$2023$，$2025$，$2026$或$-2027$，$-2025$，$-2024$。
(2) 解：因为$AB = 2$，$BC = 1$，所以$AC=AB + BC=3$。
因为$A$是线段$OC$的中点，所以$OA=AC = 3$，$OC=2OA = 6$。
所以$OB=OA+AB=3 + 2=5$。
因此，点$A$表示的数是$3$，点$B$表示的数是$5$，点$C$表示的数是$6$。
(3) 解：当点$O$在点$B$左侧时，
因为$BO = 2025$，$AB=2$，$BC = 1$，
所以点$B$表示的数是$2025$，
点$A$表示的数是$2025-2=2023$，
点$C$表示的数是$2025 + 1=2026$。
当点$O$在点$B$右侧时，
因为$BO = 2025$，$AB = 2$，$BC=1$，
所以点$B$表示的数是$-2025$，
点$A$表示的数是$-2025-2=-2027$，
点$C$表示的数是$-2025 + 1=-2024$。
综上，点$A$，$B$，$C$表示的数分别为$2023$，$2025$，$2026$或$-2027$，$-2025$，$-2024$。
27. (12分)如图①,一副三角尺的边$OD$,$ON在直线AB$上,直角顶点$C$,$M分别在直线AB$的上方和下方,$∠COD = 45^{\circ}$,$∠MON = 60^{\circ}$.
(1)将图①中的三角尺$MON绕点O逆时针旋转90^{\circ}$,则$∠BOM = $______$^{\circ}$;
(2)将图①中的三角尺$MON绕点O$按逆时针方向旋转到图②的位置,使$OM在∠AOC$的内部,求$∠AON - ∠COM$的度数;
(3)将图①中的三角尺$MON$,$COD同时绕点O$按逆时针方向旋转,速度分别为每秒$15^{\circ}和每秒5^{\circ}$,当三角尺$MON$第一次旋转到起始位置时,三角尺$MON$,$COD$都停止运动.设运动时间为$t$秒,当直线$OM恰好平分∠AOC$时,求$t$的值.
(1)将图①中的三角尺$MON绕点O逆时针旋转90^{\circ}$,则$∠BOM = $______$^{\circ}$;
(2)将图①中的三角尺$MON绕点O$按逆时针方向旋转到图②的位置,使$OM在∠AOC$的内部,求$∠AON - ∠COM$的度数;
(3)将图①中的三角尺$MON$,$COD同时绕点O$按逆时针方向旋转,速度分别为每秒$15^{\circ}和每秒5^{\circ}$,当三角尺$MON$第一次旋转到起始位置时,三角尺$MON$,$COD$都停止运动.设运动时间为$t$秒,当直线$OM恰好平分∠AOC$时,求$t$的值.
答案：
(1) 30 (2) 解: 因为$∠AON=60^{\circ }-∠AOM,∠COM=45^{\circ }-∠AOM,$所以$∠AON-∠COM=(60^{\circ }-∠AOM)-(45^{\circ }-∠AOM)=15^{\circ }.$ (3) 解: OM 的旋转角度为$15^{\circ }t$, OC 的旋转角度为$5^{\circ }t.$如答图①,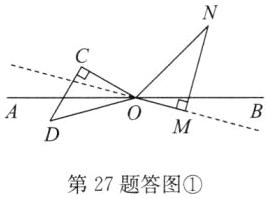
此时$60^{\circ }-15^{\circ }t=\frac {1}{2}(45^{\circ }-5^{\circ }t),$解得$t=3;$如答图②,
此时$15^{\circ }t-60^{\circ }=\frac {1}{2}(5^{\circ }t-45^{\circ }),$解得$t=3.$但当$t=3$时,$5^{\circ }t-45^{\circ }＜0$, 不符合实际, 舍去;如答图③,
此时$15^{\circ }t-180^{\circ }-60^{\circ }=\frac {1}{2}(5^{\circ }t-45^{\circ }),$解得$t=17.4.$综上,$t=3$或$t=17.4.$
(1) 30 (2) 解: 因为$∠AON=60^{\circ }-∠AOM,∠COM=45^{\circ }-∠AOM,$所以$∠AON-∠COM=(60^{\circ }-∠AOM)-(45^{\circ }-∠AOM)=15^{\circ }.$ (3) 解: OM 的旋转角度为$15^{\circ }t$, OC 的旋转角度为$5^{\circ }t.$如答图①,
此时$60^{\circ }-15^{\circ }t=\frac {1}{2}(45^{\circ }-5^{\circ }t),$解得$t=3;$如答图②, 此时$15^{\circ }t-60^{\circ }=\frac {1}{2}(5^{\circ }t-45^{\circ }),$解得$t=3.$但当$t=3$时,$5^{\circ }t-45^{\circ }＜0$, 不符合实际, 舍去;如答图③, 此时$15^{\circ }t-180^{\circ }-60^{\circ }=\frac {1}{2}(5^{\circ }t-45^{\circ }),$解得$t=17.4.$综上,$t=3$或$t=17.4.$