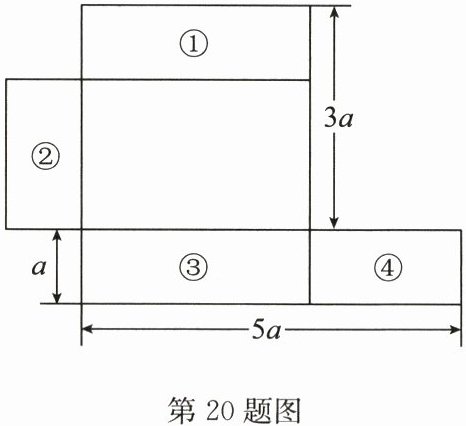
20. (8分)一个无盖的长方体盒子的展开图如图所示.
(1)该盒子的底面的长为______;(用含$a$的式子表示)
(2)若①,②,③,④四个面上分别标有整式$2(x + 1)$,$x$,$-2$,$4$,且该盒子的相对两个面上的整式的和相等,求$x$的值;
(3)请在图中补充一个长方形,使该展开图折叠成长方体盒子后有盖.
(1)该盒子的底面的长为______;(用含$a$的式子表示)
(2)若①,②,③,④四个面上分别标有整式$2(x + 1)$,$x$,$-2$,$4$,且该盒子的相对两个面上的整式的和相等,求$x$的值;
(3)请在图中补充一个长方形,使该展开图折叠成长方体盒子后有盖.

答案:
(1) 3a (2) 解: 因为①, ②, ③, ④四个面上分别标有整式$2(x+1),x,-2,4$, 且该盒子的相对两个面上的整式的和相等,所以$2(x+1)+(-2)=x+4,$解得$x=4.$ (3) 解: 如答图所示. (答案不唯一)
(1) 3a (2) 解: 因为①, ②, ③, ④四个面上分别标有整式$2(x+1),x,-2,4$, 且该盒子的相对两个面上的整式的和相等,所以$2(x+1)+(-2)=x+4,$解得$x=4.$ (3) 解: 如答图所示. (答案不唯一)

21. (8分)如图,$P是∠AOB的边OB$上的一点,点$A$,$O$,$P$都在格点上,在方格纸上按要求画图,并标注相应的字母.
(1)过点$P画OB$的垂线,交$OA于点C$;过点$P画OA$的垂线,垂足为$D$.并完成填空:
①线段______的长度表示点$P到直线OA$的距离;
②$PC$______$OC$.(填“$>$”“$<$”或“$=$”)
(2)过点$A画OB的平行线AE$.

(1)过点$P画OB$的垂线,交$OA于点C$;过点$P画OA$的垂线,垂足为$D$.并完成填空:
①线段______的长度表示点$P到直线OA$的距离;
②$PC$______$OC$.(填“$>$”“$<$”或“$=$”)
(2)过点$A画OB的平行线AE$.

答案:
解: (1) 如答图. ① PD ② (2) 如答图.
(2) 如答图.
解: (1) 如答图. ① PD ②
 (2) 如答图.
(2) 如答图.22. (6分)如图,已知线段$AB = 4$,延长$AB到点C$,使$BC= \frac{1}{2}AB$,反向延长$AB到点D$,使$AD= \frac{1}{2}AC$.
(1)求线段$CD$的长;
(2)若$Q为AB$的中点,$P为线段CD$上一点,且$BP= \frac{1}{2}BC$,求线段$PQ$的长.

(1)求线段$CD$的长;
(2)若$Q为AB$的中点,$P为线段CD$上一点,且$BP= \frac{1}{2}BC$,求线段$PQ$的长.

答案:解: (1) 因为$AB=4,BC=\frac {1}{2}AB,$所以$BC=\frac {1}{2}×4=2,$所以$AC=AB+BC=4+2=6.$因为$AD=\frac {1}{2}AC,$所以$AD=\frac {1}{2}×6=3,$所以$CD=AD+AC=3+6=9.$ (2) 因为$AB=4$, Q 为 AB 的中点,所以$QB=\frac {1}{2}AB=\frac {1}{2}×4=2.$因为$BC=2,$所以$BP=\frac {1}{2}BC=\frac {1}{2}×2=1.$当点 P 在点 B 右侧时,$PQ=QB+BP=2+1=3;$当点 P 在点 B 左侧时,$PQ=QB-BP=2-1=1.$综上, 线段 PQ 的长为 1 或 3.
23. (6分)规定一种新运算法则:$a\otimes b = a^{2}-ab$.例如,$2\otimes3 = 2^{2}-2×3 = - 2$.请用上述运算法则求下面各式的值.
(1)$(-3)\otimes(-4)$; (2)$4\otimes(2\otimes9)$.
(1)$(-3)\otimes(-4)$; (2)$4\otimes(2\otimes9)$.
答案:解: (1) 因为$a\otimes b=a^{2}-ab,$所以$(-3)\otimes (-4)=(-3)^{2}-(-3)×(-4)=9-12=-3.$ (2)$4\otimes (2\otimes 9)=4\otimes (2^{2}-2×9)=4\otimes (-14)=4^{2}-4×(-14)=16+56=72.$