1. (2024·海安月考)【探索与解决】
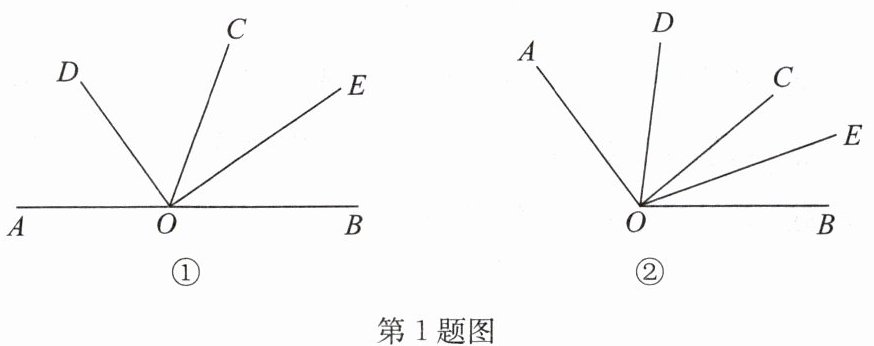
如图①,点A,O,B在同一条直线上,射线OD,OE分别平分∠AOC和∠BOC。
(1)写出与∠AOD互余的角是______
(2)写出与∠AOD互补的角是______
(3)∠DOE的度数是多少?请简单写出理由。
【拓展与延伸】
如图②,点A,O,B不在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC。
请你直接写出∠DOE与∠AOB的数量关系。
如图①,点A,O,B在同一条直线上,射线OD,OE分别平分∠AOC和∠BOC。
(1)写出与∠AOD互余的角是______
∠COE,∠BOE
;(2)写出与∠AOD互补的角是______
∠BOD
;(3)∠DOE的度数是多少?请简单写出理由。
解:$∠DOE=90^{\circ }$.理由:因为射线 OD 和射线 OE 分别平分$∠AOC$和$∠BOC$,所以$∠COD=∠AOD=\frac {1}{2}∠AOC,∠COE=∠BOE=\frac {1}{2}∠BOC$,所以$∠COD+∠COE=\frac {1}{2}∠AOC+\frac {1}{2}∠BOC=\frac {1}{2}(∠AOC+∠BOC)=\frac {1}{2}×180^{\circ }=90^{\circ }$,所以$∠DOE=90^{\circ }$.
【拓展与延伸】
如图②,点A,O,B不在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC。
请你直接写出∠DOE与∠AOB的数量关系。
$∠DOE=\frac {1}{2}∠AOB$

答案:1.【探索与解决】(1)$∠COE,∠BOE$(2)$∠BOD$(3)解:$∠DOE=90^{\circ }$.理由:因为射线 OD 和射线 OE 分别平分$∠AOC$和$∠BOC$,所以$∠COD=∠AOD=\frac {1}{2}∠AOC,∠COE=∠BOE=\frac {1}{2}∠BOC$,所以$∠COD+∠COE=\frac {1}{2}∠AOC+\frac {1}{2}∠BOC=\frac {1}{2}(∠AOC+∠BOC)=\frac {1}{2}×180^{\circ }=90^{\circ }$,所以$∠DOE=90^{\circ }$.【拓展与延伸】解:因为射线 OD 和射线 OE 分别平分$∠AOC$和$∠BOC$,所以$∠COD=∠AOD=\frac {1}{2}∠AOC,∠COE=∠BOE=\frac {1}{2}∠BOC$,所以$∠COD+∠COE=\frac {1}{2}∠AOC+\frac {1}{2}∠BOC=\frac {1}{2}∠AOB$,即$∠DOE=\frac {1}{2}∠AOB$.
2. 如图,点O在直线AB上,OC⊥AB。在三角形ODE中,∠ODE= 90°,∠DOE= 30°,先将三角形ODE的一边OE与OC重合,如图①,然后将三角形ODE绕点O按顺时针方向旋转,如图②,当OE与OB重合时停止旋转。
(1)当∠AOD= 80°时,旋转角∠COE的度数为______
(2)当OD在OC与OB之间时,求∠AOD-∠COE的度数;
(3)在三角形ODE的旋转过程中,当∠AOE= 4∠COD时,求旋转角∠COE的度数。
(1)当∠AOD= 80°时,旋转角∠COE的度数为______
20°
;(2)当OD在OC与OB之间时,求∠AOD-∠COE的度数;
解:$∠AOD-∠COE=(∠AOC+∠COD)-(∠COD+∠DOE)=∠AOC+∠COD-∠COD-∠DOE=∠AOC-∠DOE=90^{\circ }-30^{\circ }=60^{\circ }$.
(3)在三角形ODE的旋转过程中,当∠AOE= 4∠COD时,求旋转角∠COE的度数。
解:设$∠COE=x$,当 OD 在 OA 与 OC 之间时,$∠AOE=∠AOC+∠COE=90^{\circ }+x,∠COD=30^{\circ }-x$,由题意,得$90^{\circ }+x=4(30^{\circ }-x)$,解得$x=6^{\circ }$;当 OD 在 OC 与 OB 之间时,$∠AOE=∠AOC+∠COE=90^{\circ }+x,∠COD=x-30^{\circ }$,由题意,得$90^{\circ }+x=4(x-30^{\circ })$,解得$x=70^{\circ }$.综上所述,当$∠AOE=4∠COD$时,旋转角$∠COE$的度数为$6^{\circ }$或$70^{\circ }$.
答案:2.(1)$20^{\circ }$(2)解:$∠AOD-∠COE=(∠AOC+∠COD)-(∠COD+∠DOE)=∠AOC+∠COD-∠COD-∠DOE=∠AOC-∠DOE=90^{\circ }-30^{\circ }=60^{\circ }$. (3)解:设$∠COE=x$,当 OD 在 OA 与 OC 之间时,$∠AOE=∠AOC+∠COE=90^{\circ }+x,∠COD=30^{\circ }-x$,由题意,得$90^{\circ }+x=4(30^{\circ }-x)$,解得$x=6^{\circ }$;当 OD 在 OC 与 OB 之间时,$∠AOE=∠AOC+∠COE=90^{\circ }+x,∠COD=x-30^{\circ }$,由题意,得$90^{\circ }+x=4(x-30^{\circ })$,解得$x=70^{\circ }$.综上所述,当$∠AOE=4∠COD$时,旋转角$∠COE$的度数为$6^{\circ }$或$70^{\circ }$.
解析:
(1)$20^{\circ }$
(2)解:$\angle AOD - \angle COE = (\angle AOC + \angle COD) - (\angle COD + \angle DOE)$
$= \angle AOC + \angle COD - \angle COD - \angle DOE$
$= \angle AOC - \angle DOE$
$= 90^{\circ } - 30^{\circ } = 60^{\circ }$
(3)解:设$\angle COE = x$
当$OD$在$OA$与$OC$之间时,$\angle AOE = \angle AOC + \angle COE = 90^{\circ } + x$,$\angle COD = 30^{\circ } - x$
由题意得$90^{\circ } + x = 4(30^{\circ } - x)$
解得$x = 6^{\circ }$
当$OD$在$OC$与$OB$之间时,$\angle AOE = \angle AOC + \angle COE = 90^{\circ } + x$,$\angle COD = x - 30^{\circ }$
由题意得$90^{\circ } + x = 4(x - 30^{\circ })$
解得$x = 70^{\circ }$
综上所述,$\angle COE$的度数为$6^{\circ }$或$70^{\circ }$
(2)解:$\angle AOD - \angle COE = (\angle AOC + \angle COD) - (\angle COD + \angle DOE)$
$= \angle AOC + \angle COD - \angle COD - \angle DOE$
$= \angle AOC - \angle DOE$
$= 90^{\circ } - 30^{\circ } = 60^{\circ }$
(3)解:设$\angle COE = x$
当$OD$在$OA$与$OC$之间时,$\angle AOE = \angle AOC + \angle COE = 90^{\circ } + x$,$\angle COD = 30^{\circ } - x$
由题意得$90^{\circ } + x = 4(30^{\circ } - x)$
解得$x = 6^{\circ }$
当$OD$在$OC$与$OB$之间时,$\angle AOE = \angle AOC + \angle COE = 90^{\circ } + x$,$\angle COD = x - 30^{\circ }$
由题意得$90^{\circ } + x = 4(x - 30^{\circ })$
解得$x = 70^{\circ }$
综上所述,$\angle COE$的度数为$6^{\circ }$或$70^{\circ }$