1. 填一填。
(1) $\frac{3}{8}×($
(1) $\frac{3}{8}×($
$\frac{8}{3}$
$)= 7×($$\frac{1}{7}$
$)= \frac{6}{5}×($$\frac{5}{6}$
$)= 1$答案:(1)$\frac{8}{3}$ $\frac{1}{7}$ $\frac{5}{6}$
(2) 20 米的绸带,若用去 $\frac{3}{5}$ 米,则还剩(
$19\frac{2}{5}$
)米;若用去一些后还剩 $\frac{3}{5}$,则还剩(12
)米。答案:(2)$19\frac{2}{5}$ 12
解析:
$20-\frac{3}{5}=19\frac{2}{5}$
$20×\frac{3}{5}=12$
$20×\frac{3}{5}=12$
(3) 先找规律,再填数。
① $\frac{5}{8},\frac{1}{8},\frac{1}{40},$(
② $\frac{3}{2},1,\frac{2}{3},\frac{4}{9},$(
① $\frac{5}{8},\frac{1}{8},\frac{1}{40},$(
$\frac{1}{200}$
),$\frac{1}{1000}$。② $\frac{3}{2},1,\frac{2}{3},\frac{4}{9},$(
$\frac{8}{27}$
),($\frac{16}{81}$
)。答案:(3)①$\frac{1}{200}$ ②$\frac{8}{27}$ $\frac{16}{81}$
2. 选一选。
(1) 3 公顷的 $\frac{3}{5}$ 与 9 公顷的 $\frac{1}{5}$ 相比,(
A.3 公顷的 $\frac{3}{5}$ 大
B.9 公顷的 $\frac{1}{5}$ 大
C.一样大
D.无法确定
(1) 3 公顷的 $\frac{3}{5}$ 与 9 公顷的 $\frac{1}{5}$ 相比,(
C
)。A.3 公顷的 $\frac{3}{5}$ 大
B.9 公顷的 $\frac{1}{5}$ 大
C.一样大
D.无法确定
答案:(1)C
解析:
3公顷的$\frac{3}{5}$为$3×\frac{3}{5}=\frac{9}{5}$公顷,9公顷的$\frac{1}{5}$为$9×\frac{1}{5}=\frac{9}{5}$公顷,二者相等。
C
C
(2) (五育并举)某校三月是“学雷锋主题活动月”,少先队员们参加学雷锋志愿活动。其中,男生人数的 $\frac{4}{5}$ 和女生人数的 $\frac{2}{3}$ 相等,那么男生人数和女生人数相比,(
A.男生人数多
B.女生人数多
C.一样多
D.无法比较
B
)。A.男生人数多
B.女生人数多
C.一样多
D.无法比较
答案:(2)B
解析:
设男生人数为$x$,女生人数为$y$。
由题意得:$\frac{4}{5}x = \frac{2}{3}y$
等式两边同时乘以15(5和3的最小公倍数)得:$12x = 10y$
化简得:$6x = 5y$,即$x = \frac{5}{6}y$
因为$\frac{5}{6} < 1$,所以$x < y$,女生人数多。
B
由题意得:$\frac{4}{5}x = \frac{2}{3}y$
等式两边同时乘以15(5和3的最小公倍数)得:$12x = 10y$
化简得:$6x = 5y$,即$x = \frac{5}{6}y$
因为$\frac{5}{6} < 1$,所以$x < y$,女生人数多。
B
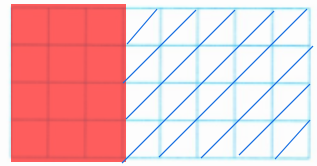
3. (数形结合)把下图中方格的 $\frac{3}{8}$ 涂上红色,$\frac{5}{8}$ 涂上蓝色,再把蓝色区域的 $\frac{3}{4}$ 画上斜线。

涂红色、画斜线的方格各有多少个?

涂红色、画斜线的方格各有多少个?
答案:
涂红色:$32×\frac{3}{8}=12$(个) 画斜线:$32×\frac{5}{8}×\frac{3}{4}=15$(个)
涂红色:$32×\frac{3}{8}=12$(个) 画斜线:$32×\frac{5}{8}×\frac{3}{4}=15$(个)

4. (生活应用)一款投影仪的原价是 1440 元,活动期间,某网店进行促销,每台直降 $\frac{1}{12}$。活动期间每台投影仪便宜了多少元? 只需付多少元?
答案:$1440×\frac{1}{12}=120$(元) $1440-120=1320$(元)
5. 小动物们需要过河,但是现在岸边只有一条小船,小猴的体重是 18 千克,小狗的体重是小猴体重的 $\frac{1}{3}$,小猫的体重是小狗体重的 $\frac{2}{3}$。它们可以同时坐船过河吗?


答案:$18×\frac{1}{3}=6$(千克) $6×\frac{2}{3}=4$(千克) $18+6+4=28$(千克) $28<30$ 可以同时坐船过河
6. 目前,某市居民用电的电价是 0.52 元/(千瓦·时)。安装分时电表的居民实行峰谷电价,收费标准如表所示:

优优家一个月用电 140 千瓦·时,谷时用电量占用电总量的 $\frac{3}{7}$。如果安装了分时电表,那么优优家这个月的电费是(

优优家一个月用电 140 千瓦·时,谷时用电量占用电总量的 $\frac{3}{7}$。如果安装了分时电表,那么优优家这个月的电费是(
65
)元。答案:65 解析:根据题意,分别求出谷时和峰时的电费,谷时电费为$140×\frac{3}{7}×0.35=21$(元)。因为谷时用电量占用电总量的$\frac{3}{7}$,所以峰时用电量占用电总量的$1-\frac{3}{7}=\frac{4}{7}$,峰时电费为$140×\frac{4}{7}×0.55=44$(元),再将两者相加即可求出优优家这个月的电费,即$21+44=65$(元)。
解析:
谷时用电量:$140×\frac{3}{7} = 60$(千瓦·时)
谷时电费:$60×0.35 = 21$(元)
峰时用电量占比:$1-\frac{3}{7}=\frac{4}{7}$
峰时用电量:$140×\frac{4}{7} = 80$(千瓦·时)
峰时电费:$80×0.55 = 44$(元)
总电费:$21 + 44 = 65$(元)
65
谷时电费:$60×0.35 = 21$(元)
峰时用电量占比:$1-\frac{3}{7}=\frac{4}{7}$
峰时用电量:$140×\frac{4}{7} = 80$(千瓦·时)
峰时电费:$80×0.55 = 44$(元)
总电费:$21 + 44 = 65$(元)
65