1 填表。
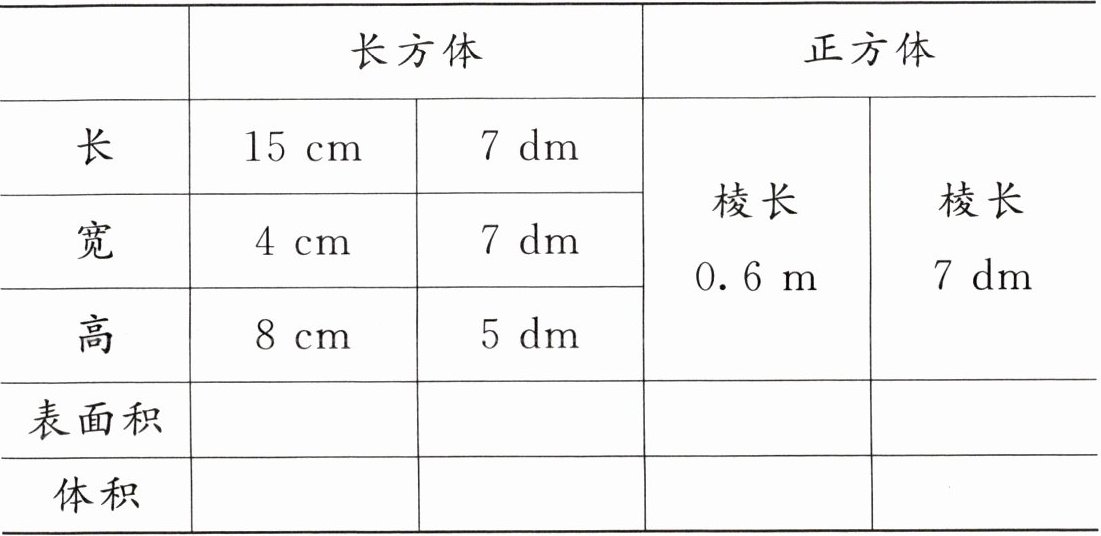

| | 长方体 | 长方体 | 正方体(棱长$0.6\ m$) | 正方体(棱长$7\ dm$) |
|---------|----------------------|----------------------|--------------------------------|--------------------------------|
| 长 | $15\ cm$ | $7\ dm$ | - | - |
| 宽 | $4\ cm$ | $7\ dm$ | - | - |
| 高 | $8\ cm$ | $5\ dm$ | - | - |
| 表面积 | $424\ cm^2$ | $238\ dm^2$ | $2.16\ m^2$ | $294\ dm^2$ |
| 体积 | $480\ cm^3$ | $245\ dm^3$ | $0.216\ m^3$ | $343\ dm^3$ |
|---------|----------------------|----------------------|--------------------------------|--------------------------------|
| 长 | $15\ cm$ | $7\ dm$ | - | - |
| 宽 | $4\ cm$ | $7\ dm$ | - | - |
| 高 | $8\ cm$ | $5\ dm$ | - | - |
| 表面积 | $424\ cm^2$ | $238\ dm^2$ | $2.16\ m^2$ | $294\ dm^2$ |
| 体积 | $480\ cm^3$ | $245\ dm^3$ | $0.216\ m^3$ | $343\ dm^3$ |
答案:长方体(第一列)
表面积:
$(15×4 + 15×8 + 4×8)×2$
$=(60 + 120 + 32)×2$
$=212×2 = 424\ cm^2$
体积:
$15×4×8 = 480\ cm^3$
长方体(第二列)
表面积:
$(7×7 + 7×5 + 7×5)×2$
$=(49 + 35 + 35)×2$
$=119×2 = 238\ dm^2$
体积:
$7×7×5 = 245\ dm^3$
正方体(第一列,棱长$0.6\ m$)
表面积:
$6×0.6×0.6 = 2.16\ m^2$
体积:
$0.6×0.6×0.6 = 0.216\ m^3$
正方体(第二列,棱长$7\ dm$)
表面积:
$6×7×7 = 294\ dm^2$
体积:
$7×7×7 = 343\ dm^3$
填表结果
| | 长方体 | 长方体 | 正方体(棱长$0.6\ m$) | 正方体(棱长$7\ dm$) |
|---------|----------------------|----------------------|--------------------------------|--------------------------------|
| 长 | $15\ cm$ | $7\ dm$ | - | - |
| 宽 | $4\ cm$ | $7\ dm$ | - | - |
| 高 | $8\ cm$ | $5\ dm$ | - | - |
| 表面积 | $424\ cm^2$ | $238\ dm^2$ | $2.16\ m^2$ | $294\ dm^2$ |
| 体积 | $480\ cm^3$ | $245\ dm^3$ | $0.216\ m^3$ | $343\ dm^3$ |
表面积:
$(15×4 + 15×8 + 4×8)×2$
$=(60 + 120 + 32)×2$
$=212×2 = 424\ cm^2$
体积:
$15×4×8 = 480\ cm^3$
长方体(第二列)
表面积:
$(7×7 + 7×5 + 7×5)×2$
$=(49 + 35 + 35)×2$
$=119×2 = 238\ dm^2$
体积:
$7×7×5 = 245\ dm^3$
正方体(第一列,棱长$0.6\ m$)
表面积:
$6×0.6×0.6 = 2.16\ m^2$
体积:
$0.6×0.6×0.6 = 0.216\ m^3$
正方体(第二列,棱长$7\ dm$)
表面积:
$6×7×7 = 294\ dm^2$
体积:
$7×7×7 = 343\ dm^3$
填表结果
| | 长方体 | 长方体 | 正方体(棱长$0.6\ m$) | 正方体(棱长$7\ dm$) |
|---------|----------------------|----------------------|--------------------------------|--------------------------------|
| 长 | $15\ cm$ | $7\ dm$ | - | - |
| 宽 | $4\ cm$ | $7\ dm$ | - | - |
| 高 | $8\ cm$ | $5\ dm$ | - | - |
| 表面积 | $424\ cm^2$ | $238\ dm^2$ | $2.16\ m^2$ | $294\ dm^2$ |
| 体积 | $480\ cm^3$ | $245\ dm^3$ | $0.216\ m^3$ | $343\ dm^3$ |
2 填空题。
$0.3\,dm^3 = $ (
$1.05\,m^3 = $ (
$4600\,dm^3 = $ (
$3500\,cm^3 = $ (
$8.09\,dm^3 = $ (
$1860\,cm^3 = $ (
$438\,mL = $ (
$0.3\,dm^3 = $ (
300
)$\,cm^3$$1.05\,m^3 = $ (
1050
)$\,dm^3$$4600\,dm^3 = $ (
4.6
)$\,m^3$$3500\,cm^3 = $ (
3.5
)$\,dm^3$$8.09\,dm^3 = $ (
8.09
)$\,L = $ (8090
)$\,mL$$1860\,cm^3 = $ (
1860
)$\,mL = $ (1.86
)$\,L$$438\,mL = $ (
438
)$\,cm^3 = $ (0.438
)$\,dm^3$答案:$0.3dm^3=(300)cm^3$;
$1.05m^3=(1050)dm^3$;
$4600dm^3=(4.6)m^3$;
$3500cm^3=(3.5)dm^3$;
$8.09dm^3=(8.09)L=(8090)mL$;
$1860cm^3=(1860)mL=(1.86)L$;
$438mL=(438)cm^3=(0.438)dm^3$。
$1.05m^3=(1050)dm^3$;
$4600dm^3=(4.6)m^3$;
$3500cm^3=(3.5)dm^3$;
$8.09dm^3=(8.09)L=(8090)mL$;
$1860cm^3=(1860)mL=(1.86)L$;
$438mL=(438)cm^3=(0.438)dm^3$。
解析:
$1 dm^3 = 1000 cm^3$,所以 $0.3 dm^3 = 0.3 × 1000 = 300 cm^3$;
$1 m^3 = 1000 dm^3$,所以 $1.05 m^3 = 1.05 × 1000 = 1050 dm^3$;
$1 m^3 = 1000 dm^3$,所以 $4600 dm^3 = 4600 ÷ 1000 = 4.6 m^3$;
$1 dm^3 = 1000 cm^3$,所以 $3500 cm^3 = 3500 ÷ 1000 = 3.5 dm^3$;
$1 dm^3 = 1 L$,$1 L = 1000 mL$,所以 $8.09 dm^3 = 8.09 L = 8.09 × 1000 = 8090 mL$;
$1 cm^3 = 1 mL$,$1 L = 1000 mL$,所以 $1860 cm^3 = 1860 mL = 1860 ÷ 1000 = 1.86 L$;
$1 mL = 1 cm^3$,$1 dm^3 = 1000 cm^3$,所以 $438 mL = 438 cm^3 = 438 ÷ 1000 = 0.438 dm^3$。
$1 m^3 = 1000 dm^3$,所以 $1.05 m^3 = 1.05 × 1000 = 1050 dm^3$;
$1 m^3 = 1000 dm^3$,所以 $4600 dm^3 = 4600 ÷ 1000 = 4.6 m^3$;
$1 dm^3 = 1000 cm^3$,所以 $3500 cm^3 = 3500 ÷ 1000 = 3.5 dm^3$;
$1 dm^3 = 1 L$,$1 L = 1000 mL$,所以 $8.09 dm^3 = 8.09 L = 8.09 × 1000 = 8090 mL$;
$1 cm^3 = 1 mL$,$1 L = 1000 mL$,所以 $1860 cm^3 = 1860 mL = 1860 ÷ 1000 = 1.86 L$;
$1 mL = 1 cm^3$,$1 dm^3 = 1000 cm^3$,所以 $438 mL = 438 cm^3 = 438 ÷ 1000 = 0.438 dm^3$。
3.挖一个蓄水量是30立方米、占地面积是25平方米的长方体水池,至少应挖多少米深?
答案:30÷25=1.2(米)
一个长方体水池,长 60 米,宽 25 米,深 2.5 米。
(1)给水池的四壁和底面抹上水泥,需要抹水泥部分的面积是多少平方米?
(2)如果向水池里灌 2 米深的水,那么这些水的体积是多少立方米?
(1)给水池的四壁和底面抹上水泥,需要抹水泥部分的面积是多少平方米?
(2)如果向水池里灌 2 米深的水,那么这些水的体积是多少立方米?
答案:$(1)$求需要抹水泥部分的面积
解:
需要抹水泥的部分为底面和四壁,可根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),但这里只算一个底面和四个侧面,即$S = ab+(ah + bh)×2$。
已知$a = 60$米,$b = 25$米,$h = 2.5$米,代入可得:
$\begin{aligned}S&=60×25+(60×2.5 + 25×2.5)×2\\&=1500+(150 + 62.5)×2\\&=1500 + 212.5×2\\&=1500 + 425\\&=1925\end{aligned}$
所以需要抹水泥部分的面积是$1925$平方米。
$(2)$求水的体积
解:
根据长方体体积公式$V = abh$(此时$h$为水的深度),已知$a = 60$米,$b = 25$米,$h = 2$米,代入可得:
$V = 60×25×2= 3000$(立方米)
所以这些水的体积是$3000$立方米。
综上,答案依次为:$(1)$$\boldsymbol{1925}$平方米;$(2)$$\boldsymbol{3000}$立方米 。
解:
需要抹水泥的部分为底面和四壁,可根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),但这里只算一个底面和四个侧面,即$S = ab+(ah + bh)×2$。
已知$a = 60$米,$b = 25$米,$h = 2.5$米,代入可得:
$\begin{aligned}S&=60×25+(60×2.5 + 25×2.5)×2\\&=1500+(150 + 62.5)×2\\&=1500 + 212.5×2\\&=1500 + 425\\&=1925\end{aligned}$
所以需要抹水泥部分的面积是$1925$平方米。
$(2)$求水的体积
解:
根据长方体体积公式$V = abh$(此时$h$为水的深度),已知$a = 60$米,$b = 25$米,$h = 2$米,代入可得:
$V = 60×25×2= 3000$(立方米)
所以这些水的体积是$3000$立方米。
综上,答案依次为:$(1)$$\boldsymbol{1925}$平方米;$(2)$$\boldsymbol{3000}$立方米 。
一个长方体木块,如果从一端截去一个长 6 厘米的长方体,正好剩下一个正方体。这个正方体的表面积比原来的长方体减少了 120 平方厘米。原来的长方体体积是多少?


答案:275 立方厘米
解析:
截去长方体后减少的表面积为截去部分的侧面积,设正方体棱长为$a$厘米。
减少的表面积由4个相同长方形组成,每个长方形面积为$a×6$,则:
$4×a×6 = 120$
$24a = 120$
$a = 5$
原长方体长为$a + 6 = 5 + 6 = 11$厘米,宽和高均为$a = 5$厘米。
体积为$11×5×5 = 275$立方厘米。
275 立方厘米
减少的表面积由4个相同长方形组成,每个长方形面积为$a×6$,则:
$4×a×6 = 120$
$24a = 120$
$a = 5$
原长方体长为$a + 6 = 5 + 6 = 11$厘米,宽和高均为$a = 5$厘米。
体积为$11×5×5 = 275$立方厘米。
275 立方厘米