1 填空题。
(1)一个长方体的底面积是 70 平方厘米,高是 5 厘米,它的体积是(
(2)一个正方体的底面积是 25 平方厘米,它的表面积是(
(3)一个长方体蓄水池,占地 15 平方米,池深 1.6 米,池内最多能蓄水(
(4)如果体积相等,长方体高是正方体高的一半,那长方体底面积是正方体底面积的(
(1)一个长方体的底面积是 70 平方厘米,高是 5 厘米,它的体积是(
350立方厘米
)。(2)一个正方体的底面积是 25 平方厘米,它的表面积是(
150
)平方厘米,体积是(125
)立方厘米。(3)一个长方体蓄水池,占地 15 平方米,池深 1.6 米,池内最多能蓄水(
24
)立方米。(4)如果体积相等,长方体高是正方体高的一半,那长方体底面积是正方体底面积的(
2倍
)。答案:(1) 350立方厘米
(2) 150,125
(3) 24
(4) 2倍
(2) 150,125
(3) 24
(4) 2倍
解析:
(1) 根据长方体体积公式 $V = 底面积 × 高$,代入数值计算:$V = 70 × 5 = 350$(立方厘米)。
(2) 正方体底面积为25平方厘米,所以棱长为5厘米(因为$5×5=25$),表面积 $S = 6 × 底面积 = 6 × 25 = 150$(平方厘米);体积 $V = 底面积 × 高 = 25 × 5 = 125$(立方厘米)。
(3) 根据长方体体积公式,体积 $V = 底面积 × 高 = 15 × 1.6 = 24$(立方米)。
(4) 设正方体高为 $h$,则长方体高为 $\frac{h}{2}$。设正方体底面积为 $S_1$,长方体底面积为 $S_2$。由体积相等得:$S_1 × h = S_2 × \frac{h}{2}$,解得 $S_2 = 2S_1$,即长方体底面积是正方体底面积的2倍。
(2) 正方体底面积为25平方厘米,所以棱长为5厘米(因为$5×5=25$),表面积 $S = 6 × 底面积 = 6 × 25 = 150$(平方厘米);体积 $V = 底面积 × 高 = 25 × 5 = 125$(立方厘米)。
(3) 根据长方体体积公式,体积 $V = 底面积 × 高 = 15 × 1.6 = 24$(立方米)。
(4) 设正方体高为 $h$,则长方体高为 $\frac{h}{2}$。设正方体底面积为 $S_1$,长方体底面积为 $S_2$。由体积相等得:$S_1 × h = S_2 × \frac{h}{2}$,解得 $S_2 = 2S_1$,即长方体底面积是正方体底面积的2倍。
2 计算下面长方体和正方体的体积。
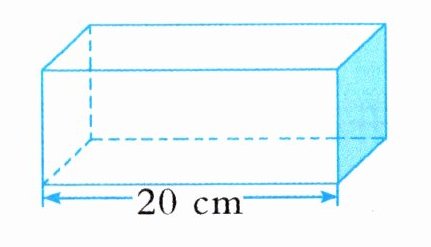
(1)长方体的侧面涂色部分的面积是$ 32 cm^2。$
(2)

(1)长方体的侧面涂色部分的面积是$ 32 cm^2。$

(2)

答案:(1)32×20=640(cm³)
(2)5×5×5=125(cm³)
(2)5×5×5=125(cm³)
1 一个长方体油箱,底面积是 15 平方分米,深 5 分米。这个油箱的容积是多少升?如果 1 升汽油重 0.75 千克,这个油箱最多可以装汽油多少千克?
答案:75 升 56.25 千克
解析:
15×5=75(立方分米)
75立方分米=75升
75×0.75=56.25(千克)
75升
56.25千克
75立方分米=75升
75×0.75=56.25(千克)
75升
56.25千克
2 一个棱长是 5 分米的正方体储水箱,储水的水面低于箱口 2 分米。这个水箱现在储水多少升?
答案:75 升
解析:
水箱底面积:$5×5 = 25$(平方分米)
水的高度:$5 - 2 = 3$(分米)
储水体积:$25×3 = 75$(立方分米)
$75$立方分米$=75$升
75升
水的高度:$5 - 2 = 3$(分米)
储水体积:$25×3 = 75$(立方分米)
$75$立方分米$=75$升
75升
3 学校运来 7.6 立方米的黄沙。现在要把这些黄沙铺在一个长 5 米、宽 3.8 米的长方体沙坑里,沙坑里的黄沙厚多少厘米?
答案:40 厘米
解析:
5×3.8=19(平方米)
7.6÷19=0.4(米)
0.4米=40厘米
40厘米
7.6÷19=0.4(米)
0.4米=40厘米
40厘米