(1)$\dfrac{5}{6}时=$(
$2.08\mathrm{L}=$(
50
)分 $\dfrac{5}{8}千克=$(625
)克$2.08\mathrm{L}=$(
2080
)$\mathrm{mL}$ $370\mathrm{cm}^3=$(0.37
)$\mathrm{dm}^3$答案:50;625;2080;0.37
解析:
1时=60分,$\dfrac{5}{6}×60=50$,所以$\dfrac{5}{6}时=50分$;1千克=1000克,$\dfrac{5}{8}×1000=625$,所以$\dfrac{5}{8}千克=625克$;1L=1000mL,$2.08×1000=2080$,所以$2.08\mathrm{L}=2080\mathrm{mL}$;1$\mathrm{dm}^3$=1000$\mathrm{cm}^3$,$370÷1000=0.37$,所以$370\mathrm{cm}^3=0.37\mathrm{dm}^3$。
(2)桃树和梨树的棵数比是$8:7$,那么梨树和桃树的棵数比是(
7:8
),桃树的棵数是梨树的$\dfrac{(8
)}{(7
)}$,梨树占总棵数的$\dfrac{(7
)}{(15
)}$,桃树占总棵数的$\dfrac{(8
)}{(15
)}$。答案:(2)梨树和桃树的棵数比是$ 7:8 $,
桃树的棵数是梨树的$\dfrac{\boxed{8}}{\boxed{7}}$,
梨树占总棵数的$\dfrac{\boxed{7}}{\boxed{15}}$,
桃树占总棵数的$\dfrac{\boxed{8}}{\boxed{15}}$。
桃树的棵数是梨树的$\dfrac{\boxed{8}}{\boxed{7}}$,
梨树占总棵数的$\dfrac{\boxed{7}}{\boxed{15}}$,
桃树占总棵数的$\dfrac{\boxed{8}}{\boxed{15}}$。
解析:
题目给出桃树和梨树的棵数比是$8:7$,可以假设桃树有$8$份,梨树有$7$份。
那么梨树和桃树的棵数比是$7:8$。
桃树的棵数是梨树的$\dfrac{8}{7}$。
总棵数为$8 + 7 = 15$份,
梨树占总棵数的$\dfrac{7}{15}$,
桃树占总棵数的$\dfrac{8}{15}$。
那么梨树和桃树的棵数比是$7:8$。
桃树的棵数是梨树的$\dfrac{8}{7}$。
总棵数为$8 + 7 = 15$份,
梨树占总棵数的$\dfrac{7}{15}$,
桃树占总棵数的$\dfrac{8}{15}$。
(3)右图是一个正方体的展开图,与$C$面相对的是(
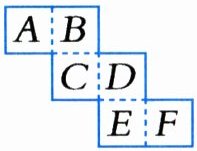
F
)面。
答案:F(在本题选项中为F对应的选项) ,即F选项为$F$面,答案选F(题目选项顺序为 A B C D E F,所以答案选F)。
解析:
正方体展开图相对面识别方法为:相隔一个正方形的两个面为相对面。
在展开图中,$A$与$D$相对,$B$与$E$相对,$C$与$F$相对,题目中无$F$选项,用$E$后面的面(即$F$)为$E$后面的隐藏面,根据展开图规律,$C$的相对面为$F$,在选项中对应$F$(题目选项以给定图形从左到右,从上到下为$A,B,C,D,E,F$)。
在展开图中,$A$与$D$相对,$B$与$E$相对,$C$与$F$相对,题目中无$F$选项,用$E$后面的面(即$F$)为$E$后面的隐藏面,根据展开图规律,$C$的相对面为$F$,在选项中对应$F$(题目选项以给定图形从左到右,从上到下为$A,B,C,D,E,F$)。
(4)在$◯$里填“$>$”“$<$”或“$=$”。
$\dfrac{4}{5}×\dfrac{1}{4}$
$\dfrac{1}{9}÷\dfrac{3}{5}$
$\dfrac{2}{7}÷\dfrac{5}{8}$
$\dfrac{4}{5}×\dfrac{1}{4}$
<
$\dfrac{4}{5}$ $\dfrac{3}{5}×\dfrac{1}{2}$<
$\dfrac{1}{2}×\dfrac{5}{3}$$\dfrac{1}{9}÷\dfrac{3}{5}$
>
$\dfrac{1}{9}$ $9÷\dfrac{5}{6}$>
$9$$\dfrac{2}{7}÷\dfrac{5}{8}$
=
$\dfrac{2}{7}×\dfrac{8}{5}$ $\dfrac{10}{11}÷\dfrac{4}{3}$<
$\dfrac{3}{4}$答案:$<$,$<$,$>$,$>$,$=$,$<$
解析:
1. 对于 $\dfrac{4}{5} × \dfrac{1}{4} ◯ \dfrac{4}{5}$:
$\dfrac{4}{5} × \dfrac{1}{4} = \dfrac{1}{5}$,因为 $\dfrac{1}{5} < \dfrac{4}{5}$,所以填 $<$。
2. 对于 $\dfrac{3}{5} × \dfrac{1}{2} ◯ \dfrac{1}{2} × \dfrac{5}{3}$:
$\dfrac{3}{5} × \dfrac{1}{2} = \dfrac{3}{10}$,$\dfrac{1}{2} × \dfrac{5}{3} = \dfrac{5}{6}$,
因为 $\dfrac{3}{10} < \dfrac{5}{6}$,所以填 $<$。
3. 对于 $\dfrac{1}{9} ÷ \dfrac{3}{5} ◯ \dfrac{1}{9}$:
$\dfrac{1}{9} ÷ \dfrac{3}{5} = \dfrac{1}{9} × \dfrac{5}{3} = \dfrac{5}{27}$,
因为 $\dfrac{5}{27} > \dfrac{1}{9} = \dfrac{3}{27}$,所以填 $>$。
4. 对于 $9 ÷ \dfrac{5}{6} ◯ 9$:
$9 ÷ \dfrac{5}{6} = 9 × \dfrac{6}{5} = \dfrac{54}{5}$,
因为 $\dfrac{54}{5} > 9$,所以填 $>$。
5. 对于 $\dfrac{2}{7} ÷ \dfrac{5}{8} ◯ \dfrac{2}{7} × \dfrac{8}{5}$:
$\dfrac{2}{7} ÷ \dfrac{5}{8} = \dfrac{2}{7} × \dfrac{8}{5}$,
两边相等,所以填 $=$。
6. 对于 $\dfrac{10}{11} ÷ \dfrac{4}{3} ◯ \dfrac{3}{4}$:
$\dfrac{10}{11} ÷ \dfrac{4}{3} = \dfrac{10}{11} × \dfrac{3}{4} = \dfrac{30}{44} = \dfrac{15}{22}$,
$\dfrac{15}{22} \approx 0.6818$,$\dfrac{3}{4} = 0.75$,
因为 $\dfrac{15}{22} < \dfrac{3}{4}$,所以填 $<$。
$\dfrac{4}{5} × \dfrac{1}{4} = \dfrac{1}{5}$,因为 $\dfrac{1}{5} < \dfrac{4}{5}$,所以填 $<$。
2. 对于 $\dfrac{3}{5} × \dfrac{1}{2} ◯ \dfrac{1}{2} × \dfrac{5}{3}$:
$\dfrac{3}{5} × \dfrac{1}{2} = \dfrac{3}{10}$,$\dfrac{1}{2} × \dfrac{5}{3} = \dfrac{5}{6}$,
因为 $\dfrac{3}{10} < \dfrac{5}{6}$,所以填 $<$。
3. 对于 $\dfrac{1}{9} ÷ \dfrac{3}{5} ◯ \dfrac{1}{9}$:
$\dfrac{1}{9} ÷ \dfrac{3}{5} = \dfrac{1}{9} × \dfrac{5}{3} = \dfrac{5}{27}$,
因为 $\dfrac{5}{27} > \dfrac{1}{9} = \dfrac{3}{27}$,所以填 $>$。
4. 对于 $9 ÷ \dfrac{5}{6} ◯ 9$:
$9 ÷ \dfrac{5}{6} = 9 × \dfrac{6}{5} = \dfrac{54}{5}$,
因为 $\dfrac{54}{5} > 9$,所以填 $>$。
5. 对于 $\dfrac{2}{7} ÷ \dfrac{5}{8} ◯ \dfrac{2}{7} × \dfrac{8}{5}$:
$\dfrac{2}{7} ÷ \dfrac{5}{8} = \dfrac{2}{7} × \dfrac{8}{5}$,
两边相等,所以填 $=$。
6. 对于 $\dfrac{10}{11} ÷ \dfrac{4}{3} ◯ \dfrac{3}{4}$:
$\dfrac{10}{11} ÷ \dfrac{4}{3} = \dfrac{10}{11} × \dfrac{3}{4} = \dfrac{30}{44} = \dfrac{15}{22}$,
$\dfrac{15}{22} \approx 0.6818$,$\dfrac{3}{4} = 0.75$,
因为 $\dfrac{15}{22} < \dfrac{3}{4}$,所以填 $<$。
(5)$\dfrac{11}{8}$与(
$\dfrac{8}{11}$
)互为倒数;$10$的倒数是($\dfrac{1}{10}$
)。答案:$\dfrac{8}{11}$;$\dfrac{1}{10}$
解析:
乘积是1的两个数互为倒数。求分数的倒数,交换分子分母位置,$\dfrac{11}{8}$的倒数是$\dfrac{8}{11}$;求整数的倒数,整数作分母,分子是1,10的倒数是$\dfrac{1}{10}$。
(6)28千米的$\dfrac{4}{7}$是(
16
)千米;(49
)千米的$\dfrac{4}{7}$是28千米。答案:$16$;$49$
解析:
1. 求$28$千米的$\frac{4}{7}$:
根据求一个数的几分之几是多少用乘法,可得$28×\frac{4}{7}=16$千米。
2. 求多少千米的$\frac{4}{7}$是$28$千米:
已知一个数的几分之几是多少,求这个数用除法,设所求数为$x$千米,则$\frac{4}{7}x = 28$,$x=28÷\frac{4}{7}=28×\frac{7}{4}=49$千米。
根据求一个数的几分之几是多少用乘法,可得$28×\frac{4}{7}=16$千米。
2. 求多少千米的$\frac{4}{7}$是$28$千米:
已知一个数的几分之几是多少,求这个数用除法,设所求数为$x$千米,则$\frac{4}{7}x = 28$,$x=28÷\frac{4}{7}=28×\frac{7}{4}=49$千米。
(7)一个长方体,长$8$厘米,宽$3$厘米,高$5$厘米,这个长方体最大的一个面的面积是(
40
)平方厘米,最小的一个面的面积是(15
)平方厘米。答案:40,15
解析:
长方体有6个面,相对的面面积相等,面积分别为长×宽、长×高、宽×高。计算各面面积:8×3=24(平方厘米),8×5=40(平方厘米),3×5=15(平方厘米)。比较得最大面面积40平方厘米,最小面面积15平方厘米。
(8)大、小两个圆的直径比为$3:2$,大圆半径与小圆半径的比是(
$3:2$
),小圆周长与大圆周长的比是($2:3$
),小圆面积与大圆面积的比是($4:9$
)。答案:(8)答案顺序为$3:2$、$2:3$、$4:9$,对应填空答案依次为第一空(3:2选项对应)、第二空(2:3选项对应)、第三空(4:9选项对应),题目为填空题直接给比值,按题目要求填比值形式即可(若原题为选择题则按选项顺序选择)。(根据题目要求直接给出比值,答案按题目空格顺序填)
解析:
设大圆直径为$3d$,小圆直径为$2d$。
大圆半径为$\frac{3d}{2}$,小圆半径为$\frac{2d}{2} = d$,半径比为$\frac{3d}{2} : d = 3:2$。
小圆周长为$2d × \pi = 2\pi d$,大圆周长为$3d × \pi = 3\pi d$,周长比为$2\pi d : 3\pi d = 2:3$。
小圆面积为$\pi d^2$,大圆面积为$\pi \left(\frac{3d}{2}\right)^2 = \frac{9}{4}\pi d^2$,面积比为$\pi d^2 : \frac{9}{4}\pi d^2 = 4:9$。
大圆半径为$\frac{3d}{2}$,小圆半径为$\frac{2d}{2} = d$,半径比为$\frac{3d}{2} : d = 3:2$。
小圆周长为$2d × \pi = 2\pi d$,大圆周长为$3d × \pi = 3\pi d$,周长比为$2\pi d : 3\pi d = 2:3$。
小圆面积为$\pi d^2$,大圆面积为$\pi \left(\frac{3d}{2}\right)^2 = \frac{9}{4}\pi d^2$,面积比为$\pi d^2 : \frac{9}{4}\pi d^2 = 4:9$。
(9)$\dfrac{2}{3}×\dfrac{5}{6}= \dfrac{(

5
)}{(9
)}$,在下图中涂色表示计算结果。
涂色略,涂10个小格即可
答案:$\dfrac{5}{9}$(涂色略,涂10个小格即可)
解析:
分数乘法计算:分子相乘的积作分子,分母相乘的积作分母,$\dfrac{2}{3}×\dfrac{5}{6}=\dfrac{2×5}{3×6}=\dfrac{10}{18}=\dfrac{5}{9}$。图中是一个3行6列的长方形,共18个小格,$\dfrac{5}{9}$即$\dfrac{10}{18}$,需涂10个小格。
(10)$\dfrac{3}{4}吨花生可以榨油\dfrac{3}{10}$吨,平均每吨花生可榨油(
$\dfrac{2}{5}$
)吨,榨$1$吨油需要花生($\dfrac{5}{2}$
)吨。答案:$\dfrac{2}{5}$,$\dfrac{5}{2}$
解析:
平均每吨花生可榨油:$\dfrac{3}{10}÷\dfrac{3}{4}=\dfrac{3}{10}×\dfrac{4}{3}=\dfrac{2}{5}$(吨);榨1吨油需要花生:$\dfrac{3}{4}÷\dfrac{3}{10}=\dfrac{3}{4}×\dfrac{10}{3}=\dfrac{5}{2}$(吨)
(11)把一根$\dfrac{4}{5}米长的绳子平均分成4$段,每段长(
$\dfrac{1}{5}$
)米,每段占全长的$\dfrac{(1
)}{(4
)}$。答案:【解析】:
(1) 求每段长度:将$\dfrac{4}{5}$米平均分成4段,每段长度为$\dfrac{4}{5} ÷ 4 = \dfrac{4}{5} × \dfrac{1}{4} = \dfrac{1}{5}$米。
(2) 求每段占全长的分数:将全长看作单位"1",平均分成4段,每段占$\dfrac{1}{4}$。
【答案】:每段长$\dfrac{1}{5}$米,每段占全长的$\dfrac{1}{4}$,因此填空为:
每段长$\boxed{\dfrac{1}{5}}$米,每段占全长的$\dfrac{\boxed{1}}{\boxed{4}}$。
(根据题目要求,最终填空答案应分别框出数字)
最终填空答案:
每段长 $\boxed{\dfrac{1}{5}}$ 米,每段占全长的 $\dfrac{\boxed{1}}{\boxed{4}}$。
(1) 求每段长度:将$\dfrac{4}{5}$米平均分成4段,每段长度为$\dfrac{4}{5} ÷ 4 = \dfrac{4}{5} × \dfrac{1}{4} = \dfrac{1}{5}$米。
(2) 求每段占全长的分数:将全长看作单位"1",平均分成4段,每段占$\dfrac{1}{4}$。
【答案】:每段长$\dfrac{1}{5}$米,每段占全长的$\dfrac{1}{4}$,因此填空为:
每段长$\boxed{\dfrac{1}{5}}$米,每段占全长的$\dfrac{\boxed{1}}{\boxed{4}}$。
(根据题目要求,最终填空答案应分别框出数字)
最终填空答案:
每段长 $\boxed{\dfrac{1}{5}}$ 米,每段占全长的 $\dfrac{\boxed{1}}{\boxed{4}}$。