算式中的□代表不为0的一个数字,观察下面的算式,
在括号里填上“可能”“不可能”或“一定”。(1)$35×□$,积的末尾( )有 0。
(2)$290×□$,积的末尾( )有 0。
(3)$33×□$,积的末尾( )有 0。
答案:1. 对于$35×□$:
因为$35 = 5×7$,当$□$为偶数($2$、$4$、$6$、$8$)时,$35×□=(5×7)×□ = 5×(7×□)$,积的末尾有$0$;当$□$为奇数($1$、$3$、$5$、$7$、$9$)时,积的末尾没有$0$。
所以$35×□$,积的末尾(可能)有$0$。
2. 对于$290×□$:
因为$290 = 29×10$,$290×□=(29×10)×□ = 29×(10×□)$,$10×□$的结果末尾一定有$0$,所以$290×□$积的末尾(一定)有$0$。
3. 对于$33×□$:
因为$33 = 3×11$,$3$和$11$都不是$2$和$5$的倍数,无论$□$取不为$0$的任何数字,$33×□$的积都不可能是$10$的倍数。
所以$33×□$,积的末尾(不可能)有$0$。
故答案依次为:可能;一定;不可能。
因为$35 = 5×7$,当$□$为偶数($2$、$4$、$6$、$8$)时,$35×□=(5×7)×□ = 5×(7×□)$,积的末尾有$0$;当$□$为奇数($1$、$3$、$5$、$7$、$9$)时,积的末尾没有$0$。
所以$35×□$,积的末尾(可能)有$0$。
2. 对于$290×□$:
因为$290 = 29×10$,$290×□=(29×10)×□ = 29×(10×□)$,$10×□$的结果末尾一定有$0$,所以$290×□$积的末尾(一定)有$0$。
3. 对于$33×□$:
因为$33 = 3×11$,$3$和$11$都不是$2$和$5$的倍数,无论$□$取不为$0$的任何数字,$33×□$的积都不可能是$10$的倍数。
所以$33×□$,积的末尾(不可能)有$0$。
故答案依次为:可能;一定;不可能。
在盒子中放 8 个球,怎样放才能达到下面的要求?(按要求画一画。)
(1)任意摸一个球,红色、黄色、蓝色、黑色四种颜色的球都有可能。

(2)任意摸一个球,摸到红色球和绿色球的可能性相同。

(1)任意摸一个球,红色、黄色、蓝色、黑色四种颜色的球都有可能。

(2)任意摸一个球,摸到红色球和绿色球的可能性相同。

答案:对于(1):
可在盒子中放红色、黄色、蓝色、黑色球各$2$个(答案不唯一,只要四种颜色球都有且数量不为$0$即可)。
对于(2):
可在盒子中放红色球和绿色球各$4$个(答案不唯一,只要红色球和绿色球数量相同即可)。
可在盒子中放红色、黄色、蓝色、黑色球各$2$个(答案不唯一,只要四种颜色球都有且数量不为$0$即可)。
对于(2):
可在盒子中放红色球和绿色球各$4$个(答案不唯一,只要红色球和绿色球数量相同即可)。
1 转动下面的转盘,结果会怎样?用线连一连。


答案:
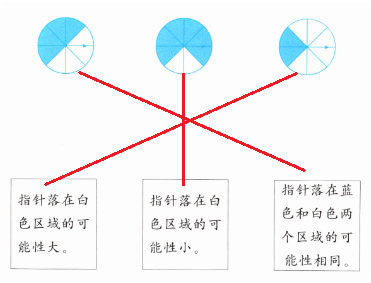

解析:
2

指针停在数字(
指针停在数字(

指针停在数字(
1
)的可能性最大。指针停在数字(
2
)的可能性最小。答案:1,2
解析:
观察转盘,数字1出现4次,数字2出现1次,数字3出现3次。4>3>1,所以指针停在数字1的可能性最大,停在数字2的可能性最小。