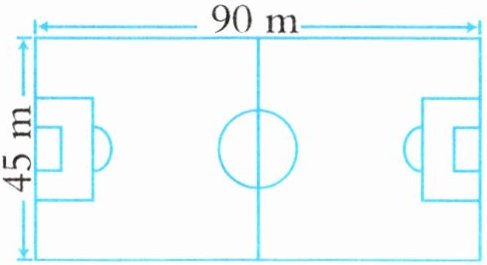
6 如果把这个足球场改建成$9$个篮球场,面积还多$270m^{2}$。一个篮球场的面积有多大?

答案:首先,计算足球场的面积:
$S_{足球场} = 长 × 宽$
$S_{足球场} = 90× 45 = 4050(m^{2})$
设一个篮球场的面积为$x m^{2}$,则9个篮球场的面积为$9x m^{2}$。
根据题意:
$9x + 270 = 4050$
$9x = 3780$
$x = 420$
答:一个篮球场的面积为$420m^{2}$。
$S_{足球场} = 长 × 宽$
$S_{足球场} = 90× 45 = 4050(m^{2})$
设一个篮球场的面积为$x m^{2}$,则9个篮球场的面积为$9x m^{2}$。
根据题意:
$9x + 270 = 4050$
$9x = 3780$
$x = 420$
答:一个篮球场的面积为$420m^{2}$。
1 小梅今年$8$岁,爸爸今年$36$岁。小梅多少岁时,爸爸的年龄是小梅的$3$倍?
答案:14 岁
解析:
设小梅$x$岁时,爸爸的年龄是小梅的$3$倍。此时爸爸的年龄为$3x$岁。
两人的年龄差不变,为$36 - 8 = 28$岁,可列方程:$3x - x = 28$
$2x = 28$
$x = 14$
14 岁
两人的年龄差不变,为$36 - 8 = 28$岁,可列方程:$3x - x = 28$
$2x = 28$
$x = 14$
14 岁
2 王老师和小明共捡了$20kg$塑料垃圾,王老师捡的塑料垃圾比小明的$2倍还多2kg$。你能求出他俩各捡了多少千克塑料垃圾吗?
答案:小明:6 kg 王老师:14 kg
解析:
设小明捡了$x$千克塑料垃圾,则王老师捡了$(2x + 2)$千克塑料垃圾。
$x + (2x + 2) = 20$
$3x + 2 = 20$
$3x = 18$
$x = 6$
王老师捡的垃圾:$2x + 2 = 2×6 + 2 = 14$(千克)
小明:6 kg,王老师:14 kg
$x + (2x + 2) = 20$
$3x + 2 = 20$
$3x = 18$
$x = 6$
王老师捡的垃圾:$2x + 2 = 2×6 + 2 = 14$(千克)
小明:6 kg,王老师:14 kg
1 填空题。
(1)把一个平行四边形沿着它的(
(2)平行四边形的面积= (
(1)把一个平行四边形沿着它的(
高
)剪开,通过平移可以把它转化成一个(长方形
),它的面积与原来平行四边形的面积(相等
)。(2)平行四边形的面积= (
底×高
),面积计算公式用字母表示为(S=ah
)。答案:(1)高;长方形;相等
(2)底$×$高;$S=ah$
(2)底$×$高;$S=ah$
解析:
(1) 对于平行四边形,可以通过沿高剪开,然后将三角形部分平移,可以转化成一个长方形,转化后的长方形面积与原来平行四边形的面积相等。
(2)平行四边形的面积计算公式是底乘以高,用字母表示,可以写成$S=ah$,其中$a$表示底,$h$表示高。
(2)平行四边形的面积计算公式是底乘以高,用字母表示,可以写成$S=ah$,其中$a$表示底,$h$表示高。
2 计算下面平行四边形的面积。


答案:答题卡:
第一个平行四边形:
公式:$面积 = 底 × 高$,
代入:$底 = 25$(厘米),$高 = 16$(厘米),
计算:$25 × 16 = 400$(平方厘米)。
第二个平行四边形:
公式:$面积 = 底 × 高$,
代入:$底 = 2$(米),$高 = 1.45$(米),
计算:$2 × 1.45 = 2.9$(平方米)。
结论:
第一个平行四边形的面积是 400 平方厘米。
第二个平行四边形的面积是 2.9 平方米。
第一个平行四边形:
公式:$面积 = 底 × 高$,
代入:$底 = 25$(厘米),$高 = 16$(厘米),
计算:$25 × 16 = 400$(平方厘米)。
第二个平行四边形:
公式:$面积 = 底 × 高$,
代入:$底 = 2$(米),$高 = 1.45$(米),
计算:$2 × 1.45 = 2.9$(平方米)。
结论:
第一个平行四边形的面积是 400 平方厘米。
第二个平行四边形的面积是 2.9 平方米。