(1)一个梯形的下底是 $3m$,上底是 $am$,高是 $hm$,它的面积是(
$(a + 3)h÷2$
)$m^{2}$。答案:$(a + 3)h÷2$
解析:
梯形面积公式为(上底+下底)×高÷2,上底是 $a$ m,下底是 $3$ m,高是 $h$ m,所以面积为 $(a + 3)h÷2$
(2)一个平行四边形的底是 $12.5dm$,高是 $6dm$,它的面积是(
75
)$dm^{2}$。答案:【解析】:平行四边形的面积公式为底乘以高,即$S = 底 × 高$。将底$12.5dm$和高$6dm$代入公式,得$S = 12.5 × 6 = 75(dm^{2})$。
【答案】:$75$(或 直接写答案框:【答案】:75)
【答案】:$75$(或 直接写答案框:【答案】:75)
(3)一个梯形的上底是 $8cm$,下底是 $12cm$,高是 $6.5cm$,它的面积是(
65
)$cm^{2}$。答案:65
解析:
梯形面积=(上底+下底)×高÷2=(8+12)×6.5÷2=20×6.5÷2=130÷2=65(cm²)
(4)在两栋教学楼之间栽树,树的棵数比间隔数(
少1
),在圆形花坛的周围植树,树的棵数和间隔数(相等
)。答案:少1,相等
解析:
在两栋教学楼之间栽树,属于两端不栽的情况,树的棵数=间隔数-1,所以树的棵数比间隔数少1;在圆形花坛周围植树,属于封闭路线植树,树的棵数=间隔数,所以树的棵数和间隔数相等。
(5)把一根 $6m$ 长的木条锯成 $2m$ 一段,一共要锯(
2
)次。答案:2
解析:
先求段数:6÷2=3(段),锯的次数=段数-1=3-1=2(次)
(6)一块三角形钢板,面积是 $36m^{2}$,量得其中一条边上的高是 $8m$,这条高对应的底是(
9
)$m$。答案:9
解析:
三角形面积公式为:面积 = 底 × 高 ÷ 2,所以底 = 面积 × 2 ÷ 高。已知面积是$36m^{2}$,高是$8m$,则底为$36×2÷8 = 72÷8 = 9(m)$。
(1)用木条钉成一个可活动的长方形木框,把它拉成平行四边形时面积与原来相比,(
A.不变
B.变大
C.变小
C
)。A.不变
B.变大
C.变小
答案:C
解析:
把一个用木条钉成的长方形木框拉成一个平行四边形,四条边的长度不变,但是高变小了(以原来长方形的一边作为平行四边形的底,拉成平行四边形后,高小于原来长方形的宽),根据平行四边形面积公式$S = 底×高$,底不变,高变小,所以面积变小。
(2)计算下面三角形的面积,正确的算式是( )。
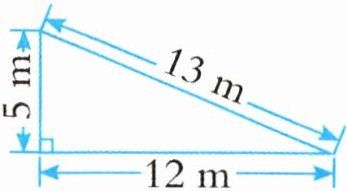
A.$12×5÷2$
B.$12×13÷2$
C.$5×13÷2$

A.$12×5÷2$
B.$12×13÷2$
C.$5×13÷2$
答案:A
解析:
三角形面积=底×高÷2,图中直角三角形的两条直角边12m和5m分别为底和高,算式为12×5÷2。
(3)两人分别从写有“先”和“后”的两张签中各抽一张,下列说法正确的是(
A.先抽的人抽到“先”的可能性大
B.后抽的人抽到“先”的可能性大
C.先抽的人和后抽的人抽到“先”的可能性相同
C
)。A.先抽的人抽到“先”的可能性大
B.后抽的人抽到“先”的可能性大
C.先抽的人和后抽的人抽到“先”的可能性相同
答案:C
解析:
本题可根据可能性的计算方法,分别分析先抽的人和后抽的人抽到“先”的可能性。
计算先抽的人抽到“先”的可能性:
已知有两张签,分别为写有“先”和“后”的签,那么先抽的人从两张签中抽一张,抽到“先”的情况只有$1$种,总共有$2$种抽法。
根据可能性的计算公式:$P(A)=\frac{m}{n}$(其中$P(A)$表示事件$A$发生的可能性,$m$表示事件$A$发生的总数,$n$是总事件发生的总数),可得先抽的人抽到“先”的可能性为$\frac{1}{2}$。
计算后抽的人抽到“先”的可能性:
若先抽的人抽到了“先”,则后抽的人抽到“先”的概率为$0$;若先抽的人抽到了“后”,则后抽的人抽到“先”的概率为$1$。
而先抽的人抽到“先”和抽到“后”的可能性均为$\frac{1}{2}$,所以后抽的人抽到“先”的可能性为$\frac{1}{2}×0 + \frac{1}{2}×1=\frac{1}{2}$。
由此可知,先抽的人和后抽的人抽到“先”的可能性相同。
计算先抽的人抽到“先”的可能性:
已知有两张签,分别为写有“先”和“后”的签,那么先抽的人从两张签中抽一张,抽到“先”的情况只有$1$种,总共有$2$种抽法。
根据可能性的计算公式:$P(A)=\frac{m}{n}$(其中$P(A)$表示事件$A$发生的可能性,$m$表示事件$A$发生的总数,$n$是总事件发生的总数),可得先抽的人抽到“先”的可能性为$\frac{1}{2}$。
计算后抽的人抽到“先”的可能性:
若先抽的人抽到了“先”,则后抽的人抽到“先”的概率为$0$;若先抽的人抽到了“后”,则后抽的人抽到“先”的概率为$1$。
而先抽的人抽到“先”和抽到“后”的可能性均为$\frac{1}{2}$,所以后抽的人抽到“先”的可能性为$\frac{1}{2}×0 + \frac{1}{2}×1=\frac{1}{2}$。
由此可知,先抽的人和后抽的人抽到“先”的可能性相同。
3. 一条街道的一边从头到尾植树 $66$ 棵,每相邻两棵树之间相隔 $4m$,这条街道有多长?
答案:答题卡:
根据题意,街道一边植树$66$棵,则相邻两棵树之间的间隔数为:
$66 - 1 = 65$(个),
每个间隔的长度为$4m$,所以街道的总长度为:
$65 × 4 = 260(m)$。
结论:
这条街道有$260m$长。
根据题意,街道一边植树$66$棵,则相邻两棵树之间的间隔数为:
$66 - 1 = 65$(个),
每个间隔的长度为$4m$,所以街道的总长度为:
$65 × 4 = 260(m)$。
结论:
这条街道有$260m$长。