9.如图,已知锐角∠AOB,画射线OC⊥OA,射线OD⊥OB,并直接写出∠AOB与∠COD
的关系.
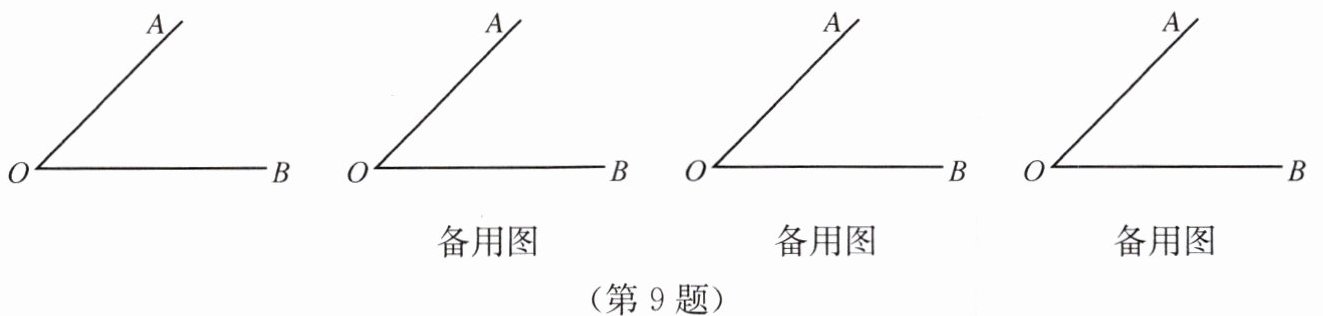
的关系.
答案：
如图①~④.∠AOB=∠COD或∠AOB+∠COD=180°
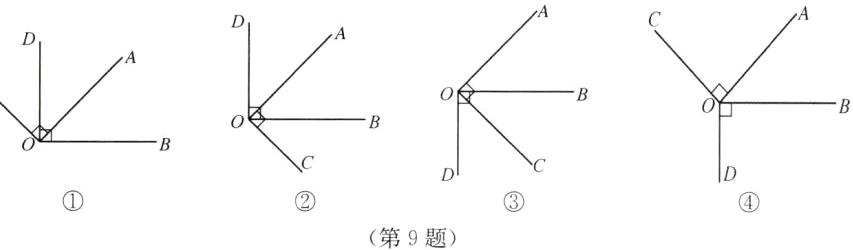
如图①~④.∠AOB=∠COD或∠AOB+∠COD=180°
10.如图,将长方形纸片的一角折叠,使顶点A落在点F处,折痕为BC.
(1)∠FBC______(填“＞”“=”或“＜”)∠ABC;
(2)如果BE是FBD的平分线,那么BE与BC有怎样的位置关系？为什么?
(3)在(2)的条件下,将BE沿BF折叠使其落在∠FBC的内部,交CF于点M,若BM
平分∠FBC,求∠FBE的大小.
(1)∠FBC______(填“＞”“=”或“＜”)∠ABC;
(2)如果BE是FBD的平分线,那么BE与BC有怎样的位置关系？为什么?
(3)在(2)的条件下,将BE沿BF折叠使其落在∠FBC的内部,交CF于点M,若BM
平分∠FBC,求∠FBE的大小.
答案：
(1)=
(2)由折叠可知∠CBA=∠CBF,所以∠CBF=$\frac{1}{2}$∠ABF,因为BE平分∠FBD,所以∠EBF =∠EBD=$\frac{1}{2}$∠DBF,又因为∠ABF+∠DBF=180°,所以∠CBF+∠EBF=
90°,即∠CBE=90°,所以BE⊥BC
(3)依照题意画出图形.如图，设∠FBE=
x°,因为BE是∠FDB的角平分线，所以∠DBF=∠FBE=x°.由翻折可知，
∠FBM=∠FBE=x°.因为BM平分∠FBC,所以∠FBC=2∠FBM=2x°.所以
∠ABC=∠FBC=2x°.又因为∠ABC+∠FBC+∠FBE+∠DBE=180°,即
2x+2x+x+x=180,x=30.所以∠FBE=30°
(1)=
(2)由折叠可知∠CBA=∠CBF,所以∠CBF=$\frac{1}{2}$∠ABF,因为BE平分∠FBD,所以∠EBF =∠EBD=$\frac{1}{2}$∠DBF,又因为∠ABF+∠DBF=180°,所以∠CBF+∠EBF=
90°,即∠CBE=90°,所以BE⊥BC
(3)依照题意画出图形.如图，设∠FBE=
x°,因为BE是∠FDB的角平分线，所以∠DBF=∠FBE=x°.由翻折可知，∠FBM=∠FBE=x°.因为BM平分∠FBC,所以∠FBC=2∠FBM=2x°.所以
∠ABC=∠FBC=2x°.又因为∠ABC+∠FBC+∠FBE+∠DBE=180°,即
2x+2x+x+x=180,x=30.所以∠FBE=30°
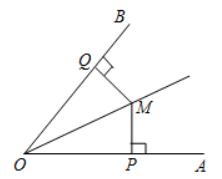
11.(1)[动手操作]如图①,已知∠AOB.
①用量角器画∠AOB的平分线OC.
②在OC上任取一点M,画MP⊥OA,MQ⊥OB,垂足分别为P,Q.
③度量点M到OA,OB的距离,你发现了什么？在OC上再取几点试一试.
(2)[实验发现]角的平分线上的点到角的两边的距离______.
(3)[结论应用]如图②,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且
PD= 3,M是射线OC上一动点,则PM的最小值是______.
①用量角器画∠AOB的平分线OC.
②在OC上任取一点M,画MP⊥OA,MQ⊥OB,垂足分别为P,Q.
③度量点M到OA,OB的距离,你发现了什么？在OC上再取几点试一试.
(2)[实验发现]角的平分线上的点到角的两边的距离______.
(3)[结论应用]如图②,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且
PD= 3,M是射线OC上一动点,则PM的最小值是______.
答案：
(1)
③经测量，可以发现MP=MQ
(2)相等
(3)3
(1)
③经测量，可以发现MP=MQ
(2)相等
(3)3