1.直线外一点与直线上各点连接的所有线段中,
垂线段
最短.答案:垂线段
2.直线外一点到这条直线的
垂线段的长度
叫作点到直线的距离.答案:垂线段的长度
3.在体育课上某同学立定跳远的情况如图所示,直线1表示起跳线,经测量,PB= 2.3m, PC= 2.2m,PD= 2.5m,则该同学立定跳远的实际成绩是
2.2
m.答案:2.2
4.如图,CD⊥AB,垂足为D,AC= 6,BC= 4,CD= 3,E是线段AB上的一个动点(包括端点),连接CE,那么CE的最小值是
3
.答案:3
5.如图,河道的一侧有甲、乙两个村庄,现要铺设一条管道将水引向甲、乙两村,下列四种方案中最节省材料的是 (
B
)答案:B
6.P为直线m外一点,A,B,C为直线m上三点,PA= 5,PB= 4,PC= 3,则点P到直线m的距离 (
A.不大于3
B.等于3
C.小于3
D.不小于3
A
)A.不大于3
B.等于3
C.小于3
D.不小于3
答案:A
解析:
点P到直线m的距离是点P到直线m的垂线段的长度,根据“垂线段最短”的性质,点P到直线m的距离小于或等于PA、PB、PC中的最小值。因为PA=5,PB=4,PC=3,其中最小值为3,所以点P到直线m的距离不大于3。
A
A
7.在直角三角形ABC中,∠ABC= 90°,AB= 3,BC= 4,AC= 5,则点B到直线AC上各点的所有线段中,最短的线段长为
$\frac{12}{5}$
.答案:$\frac{12}{5}$
解析:
在直角三角形中,点到直线的最短距离为垂线段的长度。
已知直角三角形$ABC$中,$\angle ABC = 90^\circ$,$AB = 3$,$BC = 4$,$AC = 5$。
设点$B$到直线$AC$的距离为$h$。
根据三角形面积公式,$S_{\triangle ABC} = \frac{1}{2} × AB × BC = \frac{1}{2} × AC × h$。
即$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × h$,解得$h = \frac{12}{5}$。
$\frac{12}{5}$
已知直角三角形$ABC$中,$\angle ABC = 90^\circ$,$AB = 3$,$BC = 4$,$AC = 5$。
设点$B$到直线$AC$的距离为$h$。
根据三角形面积公式,$S_{\triangle ABC} = \frac{1}{2} × AB × BC = \frac{1}{2} × AC × h$。
即$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × h$,解得$h = \frac{12}{5}$。
$\frac{12}{5}$
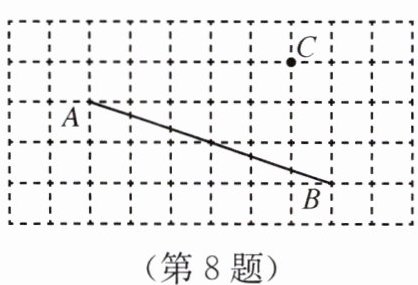
8.利用网格画图:
(1)过点C画AB的垂线,垂足为E;
(2)线段CE的长度是点C到直线______的距离;
(3)连接CA,CB,在线段CA,CB,CE中,线段______最短.
(1)过点C画AB的垂线,垂足为E;
(2)线段CE的长度是点C到直线______的距离;
(3)连接CA,CB,在线段CA,CB,CE中,线段______最短.

答案:
(1)如图所示即为所求垂足E
(2)AB
(3)CE

(1)如图所示即为所求垂足E
(2)AB
(3)CE
