9. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC= 30°时,∠BOD的大小是
60°或120°
.答案:60°或120°
解析:
情况一:射线OC,OD在直线AB同侧
∵OC⊥OD
∴∠COD=90°
∵∠AOC=30°
∴∠AOD=∠AOC+∠COD=30°+90°=120°
∵点O在直线AB上
∴∠AOD+∠BOD=180°
∴∠BOD=180°-∠AOD=180°-120°=60°
情况二:射线OC,OD在直线AB异侧
∵OC⊥OD
∴∠COD=90°
∵∠AOC=30°,点O在直线AB上
∴∠COB=180°-∠AOC=180°-30°=150°
∴∠BOD=∠COB-∠COD=150°-90°=60°
综上,∠BOD的大小是60°或120°
60°或120°
∵OC⊥OD
∴∠COD=90°
∵∠AOC=30°
∴∠AOD=∠AOC+∠COD=30°+90°=120°
∵点O在直线AB上
∴∠AOD+∠BOD=180°
∴∠BOD=180°-∠AOD=180°-120°=60°
情况二:射线OC,OD在直线AB异侧
∵OC⊥OD
∴∠COD=90°
∵∠AOC=30°,点O在直线AB上
∴∠COB=180°-∠AOC=180°-30°=150°
∴∠BOD=∠COB-∠COD=150°-90°=60°
综上,∠BOD的大小是60°或120°
60°或120°
10. 在如图所示的方格纸中,每个小正方形的边长为1.(请利用网格作图,画出的线请用铅笔描粗描黑)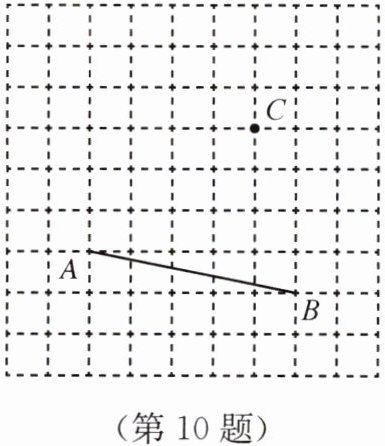
(1)过点C画AB的垂线,垂足为E;
(2)连接AC,BC,则三角形ABC的面积为______.

(1)过点C画AB的垂线,垂足为E;
(2)连接AC,BC,则三角形ABC的面积为______.
答案:
(1)如图所示,点E即为所求
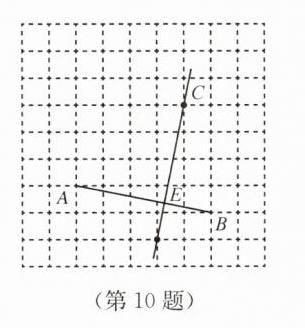
(2)9.5
(1)如图所示,点E即为所求

(2)9.5
11. 如图,直线AB与CD相交于点O,OM⊥AB.
(1)若∠1= ∠2,判断ON与CD的位置关系,并说明理由;
(2)若$∠1= \frac{1}{4}∠BOC,$求∠BOD的大小.

(1)若∠1= ∠2,判断ON与CD的位置关系,并说明理由;
(2)若$∠1= \frac{1}{4}∠BOC,$求∠BOD的大小.
答案:
(1)ON⊥CD.因为OM⊥AB,所以∠AOM=90°,∠1+∠AOC=90°;因为∠1=∠2,所以∠2+∠AOC =90°,∠NOC=90°,所以ON⊥CD
(2)∠BOD=60°.因为OM⊥AB,所以∠BOM=90°,所以∠BOC=∠BOM+∠1=90°+∠1,又因为∠1= $\frac{1}{4}$∠BOC,所以∠1=30°,∠BOC=120°,所以∠BOD=180°-∠BOC =180°-120°=60°
(1)ON⊥CD.因为OM⊥AB,所以∠AOM=90°,∠1+∠AOC=90°;因为∠1=∠2,所以∠2+∠AOC =90°,∠NOC=90°,所以ON⊥CD
(2)∠BOD=60°.因为OM⊥AB,所以∠BOM=90°,所以∠BOC=∠BOM+∠1=90°+∠1,又因为∠1= $\frac{1}{4}$∠BOC,所以∠1=30°,∠BOC=120°,所以∠BOD=180°-∠BOC =180°-120°=60°
12. 如图,已知OE⊥AB,垂足为O,直线CD经过点O.
(1)若∠AOD= 35°,求∠COE的大小;
(2)若$∠BOC= \frac{2}{3}∠COE,$求∠DOE的大小;
(3)在(2)的条件下,过点O作OF⊥CD,则∠EOF= ______.(直接写出答案)
(1)
(2)
(3)

(1)若∠AOD= 35°,求∠COE的大小;
(2)若$∠BOC= \frac{2}{3}∠COE,$求∠DOE的大小;
(3)在(2)的条件下,过点O作OF⊥CD,则∠EOF= ______.(直接写出答案)
(1)
55°
(2)
126°
(3)
36°或144°
答案:
(1)因为∠AOD与∠BOC是对顶角,且∠AOD=35°,所以∠BOC=∠AOD=35°.因为OE⊥AB,所以∠BOE=90°,所以∠COE=∠BOE-∠BOC=90°-35°=55°
(2)因为∠BOC= $\frac{2}{3}$∠COE,且∠BOC+∠COE=∠BOE=90°,所以∠COE=54°.所以∠DOE=180°-∠COE=180°-54°=126°
(3)36°或144°
(1)因为∠AOD与∠BOC是对顶角,且∠AOD=35°,所以∠BOC=∠AOD=35°.因为OE⊥AB,所以∠BOE=90°,所以∠COE=∠BOE-∠BOC=90°-35°=55°
(2)因为∠BOC= $\frac{2}{3}$∠COE,且∠BOC+∠COE=∠BOE=90°,所以∠COE=54°.所以∠DOE=180°-∠COE=180°-54°=126°
(3)36°或144°