8. 如图,已知直线 AB,CD 被直线 EF 所截,如果$\angle BMN= \angle DNF,$$\angle 1= \angle 2,$那么 MQ//NP.为什么?
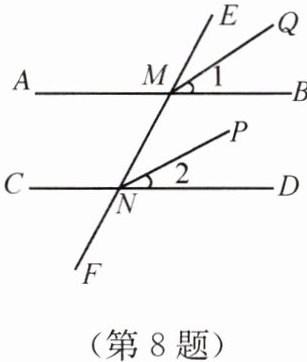

答案:平行.因为∠BMN=∠DNF,∠1=∠2(已知),所以∠BMN+∠1=∠DNF+∠2,即∠PNF=∠QMN,所以 MQ//NP(同位角相等,两直线平行)
9. 如图,在三角形 ABC 中,$\angle B= \angle ACB,$点 D,F 分别在边 BC,AC 的延长线上,作射线 CE,如果 CD 平分$\angle ECF,$那么 AB 与 CE 平行吗?为什么?


答案:AB//CE.因为 CD 平分∠ECF,所以∠DCF=∠DCE.又因为∠DCF=∠ACB,所以∠ACB=∠DCE.又因为∠B=∠ACB,所以∠B=∠DCE.所以 AB//CE
10. 如图,$\angle B 与\angle BCD $互为余角,$\angle B= \angle ACD,$$DE\perp BC,$垂足为 E,AC 与 DE 平行吗?为什么?


答案:AC//DE.因为∠B=∠ACD,∠B+∠BCD=90°,所以∠ACD+∠BCD=90°,即∠ACB=90°,因为 DE⊥BC,所以∠DEB=90°=∠ACB,所以 AC//DE
11. 如图,a,b,c 三根木棒钉在一起,交点分别为 A,B,$\angle 1= 70^\circ,$$\angle 2= 100^\circ.$现将木棒 a,b 分别绕点 A,B 顺时针旋转,同时开始,速度分别为$ 12^\circ/s 和 2^\circ/s,$两根木棒各自转满了一周就停止转动.转动

3 s 或21 s 或 75 s 或 165 s
s 时,木棒 a,b 平行.
答案:3 s 或21 s 或 75 s 或 165 s
解析:
设转动$ t $秒时,木棒$ a $,$ b $平行。
木棒$ a $绕点$ A $顺时针旋转,速度为$ 12^\circ/s $,$ t $秒后旋转角度为$ 12t^\circ $,与直线$ c $的夹角为$ 180^\circ - (12t^\circ - 100^\circ) = 280^\circ - 12t^\circ $(考虑旋转一周内的情况)。
木棒$ b $绕点$ B $顺时针旋转,速度为$ 2^\circ/s $,$ t $秒后旋转角度为$ 2t^\circ $,与直线$ c $的夹角为$ 70^\circ + 2t^\circ $(考虑旋转一周内的情况)。
当木棒$ a $,$ b $平行时,同位角相等或同旁内角互补,即:
1. $ 280^\circ - 12t^\circ = 70^\circ + 2t^\circ + 360^\circ k $($ k $为整数),解得$ t = 15^\circ - 25.71^\circ k $,当$ k = 0 $时,$ t = 15 $(不符合,舍去);当$ k = -1 $时,$ t = 21 $。
2. $ 280^\circ - 12t^\circ + 70^\circ + 2t^\circ = 180^\circ + 360^\circ m $($ m $为整数),解得$ t = 17^\circ - 36^\circ m $,当$ m = 0 $时,$ t = 17 $(不符合,舍去);当$ m = -1 $时,$ t = 53 $(不符合,舍去);当$ m = -2 $时,$ t = 89 $(不符合,舍去);当$ m = -3 $时,$ t = 125 $(不符合,舍去);当$ m = -4 $时,$ t = 161 $(不符合,舍去);当$ m = -5 $时,$ t = 197 $(不符合,舍去)。
考虑旋转一周内($ 0 \leq t \leq 30 $,木棒$ a $转一周需$ 30 $秒;$ 0 \leq t \leq 180 $,木棒$ b $转一周需$ 180 $秒),综合可得$ t = 3 $,$ 21 $,$ 75 $,$ 165 $。
$ 3\ s $或$ 21\ s $或$ 75\ s $或$ 165\ s $
木棒$ a $绕点$ A $顺时针旋转,速度为$ 12^\circ/s $,$ t $秒后旋转角度为$ 12t^\circ $,与直线$ c $的夹角为$ 180^\circ - (12t^\circ - 100^\circ) = 280^\circ - 12t^\circ $(考虑旋转一周内的情况)。
木棒$ b $绕点$ B $顺时针旋转,速度为$ 2^\circ/s $,$ t $秒后旋转角度为$ 2t^\circ $,与直线$ c $的夹角为$ 70^\circ + 2t^\circ $(考虑旋转一周内的情况)。
当木棒$ a $,$ b $平行时,同位角相等或同旁内角互补,即:
1. $ 280^\circ - 12t^\circ = 70^\circ + 2t^\circ + 360^\circ k $($ k $为整数),解得$ t = 15^\circ - 25.71^\circ k $,当$ k = 0 $时,$ t = 15 $(不符合,舍去);当$ k = -1 $时,$ t = 21 $。
2. $ 280^\circ - 12t^\circ + 70^\circ + 2t^\circ = 180^\circ + 360^\circ m $($ m $为整数),解得$ t = 17^\circ - 36^\circ m $,当$ m = 0 $时,$ t = 17 $(不符合,舍去);当$ m = -1 $时,$ t = 53 $(不符合,舍去);当$ m = -2 $时,$ t = 89 $(不符合,舍去);当$ m = -3 $时,$ t = 125 $(不符合,舍去);当$ m = -4 $时,$ t = 161 $(不符合,舍去);当$ m = -5 $时,$ t = 197 $(不符合,舍去)。
考虑旋转一周内($ 0 \leq t \leq 30 $,木棒$ a $转一周需$ 30 $秒;$ 0 \leq t \leq 180 $,木棒$ b $转一周需$ 180 $秒),综合可得$ t = 3 $,$ 21 $,$ 75 $,$ 165 $。
$ 3\ s $或$ 21\ s $或$ 75\ s $或$ 165\ s $