1. 平行线的性质:两直线平行,同位角
相等
,内错角相等
,同旁内角互补
.答案:相等,相等,互补
2. 如图,AB//EC,下列结论不正确的是(
A.∠B= ∠ECD
B.∠A= ∠ECD
C.∠B+∠ECB= 180°
D.∠A+∠B+∠ACB= 180°
B
)A.∠B= ∠ECD
B.∠A= ∠ECD
C.∠B+∠ECB= 180°
D.∠A+∠B+∠ACB= 180°
答案:B
解析:
∵AB//EC
∴∠B=∠ECD(同位角相等),∠B+∠ECB=180°(同旁内角互补)
∵∠A+∠B+∠ACB是△ABC的内角和
∴∠A+∠B+∠ACB=180°
结论不正确的是B
3. 如图,已知直线a//b,现将含45°角的三角板放入平行线之间,两个锐角顶点分别落在两条直线上.若∠1= 23°,则∠2的大小为
68°
.答案:68°
解析:
过三角板45°角的顶点作直线c//a,
因为a//b,所以c//b,
则∠1=∠3,∠2=∠4,
因为∠3+∠4=45°,
所以∠1+∠2=45°,
因为∠1=23°,
所以∠2=45°-23°=22°。
1
因为a//b,所以c//b,
则∠1=∠3,∠2=∠4,
因为∠3+∠4=45°,
所以∠1+∠2=45°,
因为∠1=23°,
所以∠2=45°-23°=22°。
1
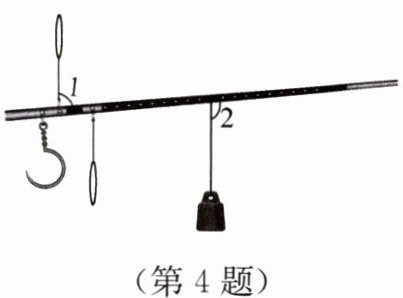
4. 一杆秤在称物时的状态如图所示,已知∠1= 85°,则∠2= ______°.

95
答案:95
5. 如图,AB//DE,BC//EF,若∠E= 107°,则∠B的大小为(
A.63°
B.73°
C.83°
D.107°
B
)A.63°
B.73°
C.83°
D.107°
答案:B
解析:
设BC与DE交于点G。
∵BC//EF,
∴∠E=∠CGE=107°(两直线平行,内错角相等)。
∵∠CGE+∠BGD=180°(邻补角互补),
∴∠BGD=180°-107°=73°。
∵AB//DE,
∴∠B=∠BGD=73°(两直线平行,内错角相等)。
B
∵BC//EF,
∴∠E=∠CGE=107°(两直线平行,内错角相等)。
∵∠CGE+∠BGD=180°(邻补角互补),
∴∠BGD=180°-107°=73°。
∵AB//DE,
∴∠B=∠BGD=73°(两直线平行,内错角相等)。
B
6. 如图,直线$l_1//l_2,BA⊥l_1,$垂足为A,则∠α+∠β的大小为(

A.150°
B.180°
C.270°
D.360°
C
) 
A.150°
B.180°
C.270°
D.360°
答案:C
解析:
过点B作BD//l₁,
∵l₁//l₂,
∴BD//l₂,
∵BA⊥l₁,
∴∠ABD=90°,
∵BD//l₂,
∴∠DBC=180°-∠α,
∵∠β=∠ABD+∠DBC,
∴∠β=90°+(180°-∠α),
∴∠α+∠β=270°.
C
∵l₁//l₂,
∴BD//l₂,
∵BA⊥l₁,
∴∠ABD=90°,
∵BD//l₂,
∴∠DBC=180°-∠α,
∵∠β=∠ABD+∠DBC,
∴∠β=90°+(180°-∠α),
∴∠α+∠β=270°.
C
7. 如图,把一张长方形纸片ABCD沿EF折叠,点D,C分别落在点M,N的位置上,EM与BC的交点为G,若∠EFC= 125°,则∠1=

70
°.
答案:70
解析:
∵四边形ABCD是长方形,
∴AD//BC,
∴∠DEF+∠EFC=180°,
∵∠EFC=125°,
∴∠DEF=180°-125°=55°,
由折叠性质得∠GEF=∠DEF=55°,
∴∠1=180°-∠GEF-∠DEF=180°-55°-55°=70°
70