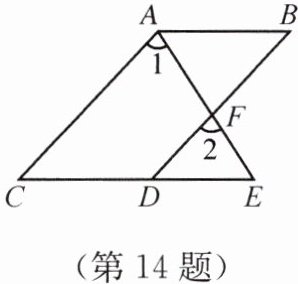
14. 如图,AE与BD相交于点F,∠B= ∠C,∠1= ∠2.
(1)AB与CE平行吗?请说明理由.
(2)若∠1= 76°,∠E= 57°,求∠B的大小.
(1)AB与CE平行吗?请说明理由.
(2)若∠1= 76°,∠E= 57°,求∠B的大小.

答案:
(1) 平行. 理由:因为∠1=∠2,所以 AC//CD,所以∠C=∠BDE. 又因为∠B=∠C,所以∠B=∠BDE,所以 AB//CE
(2) 在△AEC 中,∠1=76°,∠E=57°,所以∠C=180°-76°-57°=47°. 又因为∠B=∠C,所以∠B=47°
(1) 平行. 理由:因为∠1=∠2,所以 AC//CD,所以∠C=∠BDE. 又因为∠B=∠C,所以∠B=∠BDE,所以 AB//CE
(2) 在△AEC 中,∠1=76°,∠E=57°,所以∠C=180°-76°-57°=47°. 又因为∠B=∠C,所以∠B=47°
15. 已知:如图①,AB//CD,点P在AB,CD之间,连接AP,CP. 易说明∠APC= ∠BAP+∠PCD.
下面是两位同学添加辅助线的方法:


下面是两位同学添加辅助线的方法:


答案:以选择小明的方法为例,证明如下:因为 AB//PQ,所以∠APQ=∠BAP,又因为∠BAP=∠PMC,所以∠APQ=∠PMC,所以 PQ//CD,所以∠CPQ=∠PCD,所以∠APQ+∠CPQ=∠BAP+∠PCD,即∠APC=∠BAP+∠PCD
解析:
证明:过点P作PQ//AB,延长AP,交CD于点M。
因为AB//PQ,所以∠APQ=∠BAP。
因为AB//CD,所以∠BAP=∠PMC。
所以∠APQ=∠PMC,因此PQ//CD。
所以∠CPQ=∠PCD。
所以∠APQ+∠CPQ=∠BAP+∠PCD,即∠APC=∠BAP+∠PCD。
因为AB//PQ,所以∠APQ=∠BAP。
因为AB//CD,所以∠BAP=∠PMC。
所以∠APQ=∠PMC,因此PQ//CD。
所以∠CPQ=∠PCD。
所以∠APQ+∠CPQ=∠BAP+∠PCD,即∠APC=∠BAP+∠PCD。