9. 小明妈妈通过手机银行查询自己的账户信息,显示页面如下表所示:
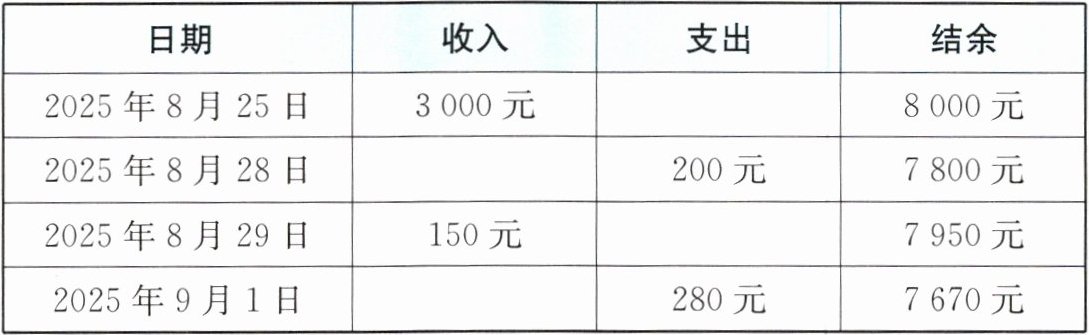
请重新设计一个银行账户信息显示页面,在栏目“交易”中同时显示收入和支出.

请重新设计一个银行账户信息显示页面,在栏目“交易”中同时显示收入和支出.
答案:


10. (1)把下列分数化成小数:$\frac{2}{5}$,$-\frac{1}{3}$,$-\frac{81}{100}$;
(2)把下列小数化成分数:$4.5$,$-3.25$,$-0.33$.
(2)把下列小数化成分数:$4.5$,$-3.25$,$-0.33$.
答案:(1)0.4,-0.$\dot{3}$,-0.81 (2)$\frac{9}{2}$,-$\frac{13}{4}$,-$\frac{33}{100}$
解析:
(1)$\frac{2}{5}=0.4$,$-\frac{1}{3}=-0.\dot{3}$,$-\frac{81}{100}=-0.81$;
(2)$4.5=\frac{9}{2}$,$-3.25=-\frac{13}{4}$,$-0.33=-\frac{33}{100}$
11. 筷子是我国的传统餐具. 其中筷子的标准长度是240 mm,该产品的合格标准是“240 mm±2 mm”,这里的“240 mm±2 mm”表示什么?
答案:表示该筷子的合格范围是238~242 mm
12. 阅读与探究.
整数和分数统称为“有理数”,为什么叫“有理数”呢?有理数的英文是“rational number”,“rational”的词根“ratio”源于古希腊,是“比率”的意思,“比”的古汉语接近“理”. 所谓有理数,就是可以写成两个整数之比,即分数形式的数.
(1)【探究】$0.\dot{5}$是不是有理数?$0.\dot{5}= 0.555…①$,$0.\dot{5}×10= 5.555…②$. 由②$-$①,得$9×0.\dot{5}= 5$,所以$0.\dot{5}= \frac{5}{9}$. 由此得$0.\dot{5}$
(2)【类比】把下列各数化成分数形式:①$0.\dot{7}$
(3)【应用】在$-1$,$\frac{22}{7}$,$0$,$0.\dot{1}$,$-9$,$0.\dot{4}\dot{3}$,$16.2$中,属于非负有理数的是
整数和分数统称为“有理数”,为什么叫“有理数”呢?有理数的英文是“rational number”,“rational”的词根“ratio”源于古希腊,是“比率”的意思,“比”的古汉语接近“理”. 所谓有理数,就是可以写成两个整数之比,即分数形式的数.
(1)【探究】$0.\dot{5}$是不是有理数?$0.\dot{5}= 0.555…①$,$0.\dot{5}×10= 5.555…②$. 由②$-$①,得$9×0.\dot{5}= 5$,所以$0.\dot{5}= \frac{5}{9}$. 由此得$0.\dot{5}$
是
(填“是”或“不是”)有理数.(2)【类比】把下列各数化成分数形式:①$0.\dot{7}$
$\frac{7}{9}$
;②$0.\dot{2}\dot{3}$$\frac{23}{99}$
.(3)【应用】在$-1$,$\frac{22}{7}$,$0$,$0.\dot{1}$,$-9$,$0.\dot{4}\dot{3}$,$16.2$中,属于非负有理数的是
$\frac{22}{7}$,0,0.$\dot{1}$,0.$\dot{4}$$\dot{3}$,16.2
.答案:(1)是 (2)$\frac{7}{9}$,$\frac{23}{99}$ (3)$\frac{22}{7}$,0,0.$\dot{1}$,0.$\dot{4}$$\dot{3}$,16.2
解析:
(1)是
(2)①设$x=0.\dot{7}$,则$10x=7.\dot{7}$,$10x - x = 7$,$9x=7$,$x=\frac{7}{9}$
②设$y=0.\dot{2}\dot{3}$,则$100y=23.\dot{2}\dot{3}$,$100y - y = 23$,$99y=23$,$y=\frac{23}{99}$
(3)$\frac{22}{7}$,0,$0.\dot{1}$,$0.\dot{4}\dot{3}$,16.2
(2)①设$x=0.\dot{7}$,则$10x=7.\dot{7}$,$10x - x = 7$,$9x=7$,$x=\frac{7}{9}$
②设$y=0.\dot{2}\dot{3}$,则$100y=23.\dot{2}\dot{3}$,$100y - y = 23$,$99y=23$,$y=\frac{23}{99}$
(3)$\frac{22}{7}$,0,$0.\dot{1}$,$0.\dot{4}\dot{3}$,16.2