9. 在数轴上与-2相距2个单位长度的点表示的数为
0 或 -4
;长为2个单位长度的木条放在数轴上,最少能覆盖2
个表示整数的点,最多能覆盖3
个表示整数的点.答案:0 或 -4,2,3
10. 把下列各数在数轴上表示出来,再用“<”把它们连接起来:$-4$,$-\frac{1}{3}$,$\frac{1}{4}$,$2$,$-\frac{1}{2}$,$3.5$,$2\frac{1}{2}$.
答案:
解:如图所示
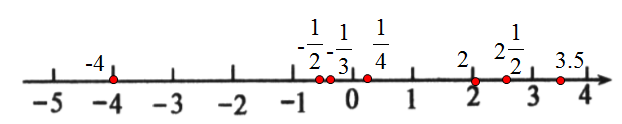
$-4<-\frac{1}{2}<-\frac{1}{3}<\frac{1}{4}<2<2\frac{1}{2}<3.5$
解:如图所示
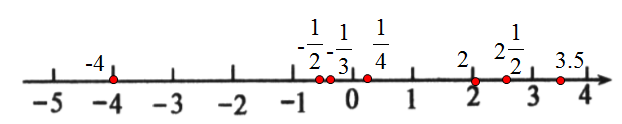
$-4<-\frac{1}{2}<-\frac{1}{3}<\frac{1}{4}<2<2\frac{1}{2}<3.5$
11. 已知a,b都是有理数,若$a<-2$,$-2<b$,则a与b哪个数大?请说明理由.
答案:根据有理数 大小关系的传递性,$b>a$
解析:
b>a,理由:由已知可得a<-2且-2<b,根据有理数大小关系的传递性,所以b>a。
12. 点A在数轴上表示+5的位置,第一次沿数轴先向右移动1个单位长度,再向左移动2个单位长度到达点$A_1$;第二次从点$A_1$开始,沿数轴先向右移动3个单位长度,再向左移动4个单位长度到达点$A_2$;第三次从点$A_2$开始,沿数轴先向右移动5个单位长度,再向左移动6个单位长度到达点$A_3$……
(1)数轴上点$A_1$表示的数是多少?
(2)数轴上点$A_3$表示的数是多少?
(3)数轴上点______表示的数是-3.
(1)数轴上点$A_1$表示的数是多少?
4
(2)数轴上点$A_3$表示的数是多少?
0
(3)数轴上点______表示的数是-3.
$A_{8}$
答案:
(1) 4
(2) 0
(3) $A_{8}$
(1) 4
(2) 0
(3) $A_{8}$
13. 阅读材料并回答问题:
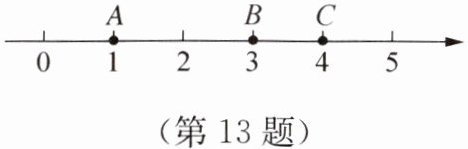
对于数轴上的三个点,若其中一个点与其他两个点的距离之间恰好满足2倍的数量关系,则称该点是其他两个点的“关联点”. 例如:如图,数轴上点A,B,C表示的数分别为1,3,4,点B与点A的距离是2,点B与点C的距离是1,此时点B是点A,C的“关联点”.
(1)若点P表示-2,点Q表示4. $-\frac{2}{3}$,0,2,6对应的点分别是$C_1$,$C_2$,$C_3$,$C_4$,则其中哪几个点是点P,Q的“关联点”?
(2)点M表示的数是-5,点N表示的数是15,P为数轴上一个动点. 若点P在点N的左侧,且点P是点M,N的“关联点”,则点P表示的数是______.
对于数轴上的三个点,若其中一个点与其他两个点的距离之间恰好满足2倍的数量关系,则称该点是其他两个点的“关联点”. 例如:如图,数轴上点A,B,C表示的数分别为1,3,4,点B与点A的距离是2,点B与点C的距离是1,此时点B是点A,C的“关联点”.

(1)若点P表示-2,点Q表示4. $-\frac{2}{3}$,0,2,6对应的点分别是$C_1$,$C_2$,$C_3$,$C_4$,则其中哪几个点是点P,Q的“关联点”?
$C_{2}$,$C_{3}$
(2)点M表示的数是-5,点N表示的数是15,P为数轴上一个动点. 若点P在点N的左侧,且点P是点M,N的“关联点”,则点P表示的数是______.
$-25$或$\frac{5}{3}$或$\frac{25}{3}$
答案:$(1) $解:$(1)C_{1}P=-\frac 23-(-2)=\frac 43,$$C_{1}Q=4-(-\frac 23)=\frac {14}{3} ,$$2C_{1}P≠C_{1}Q,$$C_{1}P≠2C_{1}Q,$
所以$C_{1}$不是点$P,$$Q $的$“$关联点$”;$
$C_{2}P=0-(-2)=2,$$C_{2}Q=4-0=4,$$2C_{2}P=C_{2}Q,$
所以$C_{2}$是点$P,$$Q $的$“$关联点$”;$
$C_{3}P=2-(-2)=4,$$C_{3}Q=4-2=2,$$C_{3}P=2C_{3}Q,$
所以$C_{3}$是点$P,$$Q $的$“$关联点$”;$
$C_{4}P=6-(-2)=8,$$C_{4}Q=6-4=2,$$2C_{4}P≠C_{4}Q,$$C_{4}P≠2C_{4}Q,$
所以$C_{4}$不是点$P,$$Q $的$“$关联点$”;$
综上所述,$C_{2},$$C_{3}$是点$P,$$Q $的$“$关联点$”.$
$(2) -25 $或$ \frac{5}{3}$或$\frac{25}{3}$