9. 现有两根长度分别为5 cm和8 cm的木棒,若第三根木棒能与它们围成三角形,则第三根木棒的长度x cm需要满足的条件是
$3 < r < 13$
.答案:$3 < r < 13$
解析:
$3 < x < 13$
10. 如图,在△ABC中,边AB的垂直平分线交AB于点D,交BC于点E,若BC= 7,AC= 6,则△AEC的周长是
13
.答案:13
解析:
∵DE是AB的垂直平分线,
∴AE=BE。
∵BC=7,AC=6,
∴△AEC的周长=AE+EC+AC=BE+EC+AC=BC+AC=7+6=13。
13
11. 如图,在△ABC中,∠C= 90°,∠A= 30°,BD是△ABC的角平分线,BD= 4,则AC的长是______.


6
答案:6
解析:
在△ABC中,∠C=90°,∠A=30°,则∠ABC=60°。
BD是∠ABC的角平分线,所以∠CBD=∠ABD=30°。
在Rt△BCD中,∠CBD=30°,BD=4,
则CD=BD·sin30°=4×$\frac{1}{2}$=2,
BC=BD·cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$。
在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,
则AB=2BC=4$\sqrt{3}$,
AC=$\sqrt{AB^2 - BC^2}$=$\sqrt{(4\sqrt{3})^2 - (2\sqrt{3})^2}$=$\sqrt{48 - 12}$=$\sqrt{36}$=6。
6
BD是∠ABC的角平分线,所以∠CBD=∠ABD=30°。
在Rt△BCD中,∠CBD=30°,BD=4,
则CD=BD·sin30°=4×$\frac{1}{2}$=2,
BC=BD·cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$。
在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,
则AB=2BC=4$\sqrt{3}$,
AC=$\sqrt{AB^2 - BC^2}$=$\sqrt{(4\sqrt{3})^2 - (2\sqrt{3})^2}$=$\sqrt{48 - 12}$=$\sqrt{36}$=6。
6
12. 如图,E是△ABC的中线AD的中点,若△ABC的面积是16,BC= 4,则点E到BC的距离是
4
.答案:4
解析:
∵AD是△ABC的中线,△ABC的面积是16
∴S△ABD = $\frac{1}{2}$S△ABC = 8
∵E是AD的中点
∴S△EBD = $\frac{1}{2}$S△ABD = 4
设点E到BC的距离是h
∵BC=4,D是BC中点
∴BD=2
∵S△EBD = $\frac{1}{2}$×BD×h
∴4 = $\frac{1}{2}$×2×h
解得h=4
4
13. 如图,在四边形ABCD中,∠BCD= 90°,BD平分∠ABC,AB= 6,BC= 9,CD= 4,则四边形ABCD的面积是
30
.答案:30
解析:
过点D作DE⊥AB交BA延长线于点E。
∵BD平分∠ABC,∠BCD=90°,DE⊥AB,
∴DE=CD=4。
S△BCD=$\frac{1}{2}$×BC×CD=$\frac{1}{2}$×9×4=18。
S△ABD=$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×6×4=12。
S四边形ABCD=S△BCD+S△ABD=18+12=30。
30
∵BD平分∠ABC,∠BCD=90°,DE⊥AB,
∴DE=CD=4。
S△BCD=$\frac{1}{2}$×BC×CD=$\frac{1}{2}$×9×4=18。
S△ABD=$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×6×4=12。
S四边形ABCD=S△BCD+S△ABD=18+12=30。
30
14. 如图,已知△ABC(AC>AB),DE= BC,以D,E为顶点作三角形,使所作的三角形与△ABC全等,这样的三角形最多可以作出
4
个.答案:4
15. 如图,在Rt△ABC中,∠C= 90°,∠B= 30°,BC= 9,P,D分别为边BC,AB上的动点,则AP+PD的最小值是______

9
.
答案:9
解析:
作点A关于BC的对称点A',连接A'D,A'B。
在Rt△ABC中,∠C=90°,∠B=30°,BC=9,
则∠BAC=60°,AC=BC·tan30°=9×$\frac{\sqrt{3}}{3}$=3$\sqrt{3}$,
AB=2AC=6$\sqrt{3}$。
因为点A与A'关于BC对称,
所以A'C=AC=3$\sqrt{3}$,∠A'CB=∠ACB=90°,
则∠A'CB+∠ACB=180°,即A、C、A'三点共线,AA'=2AC=6$\sqrt{3}$。
AP+PD=A'P+PD≥A'D(当且仅当A'、P、D三点共线时取等号)。
要使AP+PD最小,需A'D最小,此时A'D⊥AB。
在Rt△AA'D中,∠A'AD=60°,
A'D=AA'·sin60°=6$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=9。
故AP+PD的最小值是9。
在Rt△ABC中,∠C=90°,∠B=30°,BC=9,
则∠BAC=60°,AC=BC·tan30°=9×$\frac{\sqrt{3}}{3}$=3$\sqrt{3}$,
AB=2AC=6$\sqrt{3}$。
因为点A与A'关于BC对称,
所以A'C=AC=3$\sqrt{3}$,∠A'CB=∠ACB=90°,
则∠A'CB+∠ACB=180°,即A、C、A'三点共线,AA'=2AC=6$\sqrt{3}$。
AP+PD=A'P+PD≥A'D(当且仅当A'、P、D三点共线时取等号)。
要使AP+PD最小,需A'D最小,此时A'D⊥AB。
在Rt△AA'D中,∠A'AD=60°,
A'D=AA'·sin60°=6$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=9。
故AP+PD的最小值是9。
三、解答题
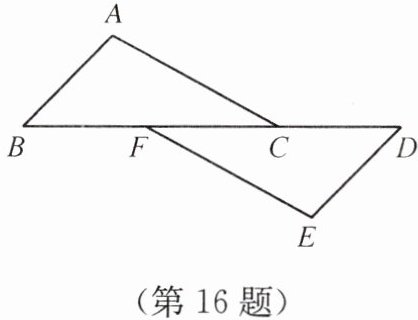
16. 如图,点F,C在BD上,BF= CD,AB//DE,AC//EF.
(1)求证:△ABC≌△EDF;
(2)若AC= 6,∠ACB= 30°,求点E到BD的距离.
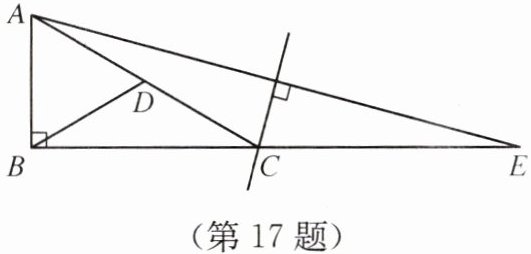
17. 如图,在△ABE中,∠ABE= 90°,∠E= 15°,AE的垂直平分线交BE于点C,连接AC,取AC的中点D.判断△ABD的形状,并说明理由.

18. 如图,D是等边三角形ABC的边AC上的一个定点,P,Q都是边AB上的动点(点P在点Q的上方),且PQ= AD.求证:CQ>PD.

19. 如图,在△ABC中,∠C= 90°,AC= 10,BC= 5,AX⊥AC,垂足为A,点P和点Q分别在线段AC和射线AX上运动,且AB= PQ,当△ABC与△APQ全等时,请说明点P的位置.
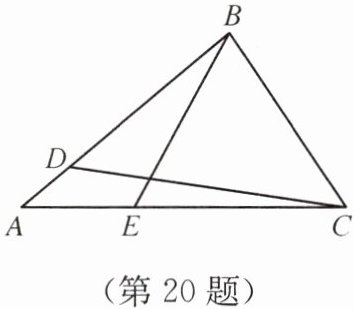
20. 如图,在△ABC中,∠A= 40°,点D,E分别在边AB,AC上,BD= BC= CE,连接CD,BE.
(1)若∠ABC= 80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的数量关系,并说明理由.

21. 如图,在△ABC中,∠ABC,∠ACB的平分线交于点M,过点M作DE//BC,与边AB,AC分别交于点D,E.
(1)若∠A= 70°,求∠BMC的度数;
(2)若△ABC的周长为m,BC的长为a,求△ADE的周长(用含m,a的代数式表示).

22. 如图,已知Rt△ABC,∠A= 90°.
(1)用直尺和圆规完成下列问题:将△ABC绕点A按顺时针方向旋转90°得到△ADE(点B,C的对应点分别为D,E),BC的延长线交DE于点F,连接BD;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若BC= 2EF,试确定△BDE的形状,并求∠ABC的大小.

16. 如图,点F,C在BD上,BF= CD,AB//DE,AC//EF.
(1)求证:△ABC≌△EDF;
(2)若AC= 6,∠ACB= 30°,求点E到BD的距离.

17. 如图,在△ABE中,∠ABE= 90°,∠E= 15°,AE的垂直平分线交BE于点C,连接AC,取AC的中点D.判断△ABD的形状,并说明理由.

18. 如图,D是等边三角形ABC的边AC上的一个定点,P,Q都是边AB上的动点(点P在点Q的上方),且PQ= AD.求证:CQ>PD.

19. 如图,在△ABC中,∠C= 90°,AC= 10,BC= 5,AX⊥AC,垂足为A,点P和点Q分别在线段AC和射线AX上运动,且AB= PQ,当△ABC与△APQ全等时,请说明点P的位置.

20. 如图,在△ABC中,∠A= 40°,点D,E分别在边AB,AC上,BD= BC= CE,连接CD,BE.
(1)若∠ABC= 80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的数量关系,并说明理由.

21. 如图,在△ABC中,∠ABC,∠ACB的平分线交于点M,过点M作DE//BC,与边AB,AC分别交于点D,E.
(1)若∠A= 70°,求∠BMC的度数;
(2)若△ABC的周长为m,BC的长为a,求△ADE的周长(用含m,a的代数式表示).

22. 如图,已知Rt△ABC,∠A= 90°.
(1)用直尺和圆规完成下列问题:将△ABC绕点A按顺时针方向旋转90°得到△ADE(点B,C的对应点分别为D,E),BC的延长线交DE于点F,连接BD;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若BC= 2EF,试确定△BDE的形状,并求∠ABC的大小.
答案:
16.
(1) $\because AB// DE$,$\therefore \angle A = \angle D$.同理$\angle ACB = \angle DFE$.$\because BF = DC$,$\therefore BF + FC = DC + FC$,即$BC = DF$.$\therefore \triangle ABC\cong \triangle EDF$
(2) 作$EP\perp BD$,垂足为点$P$,$\because \triangle ABC\cong \triangle EDF$,$\therefore EF = AC = 6$.由
(1)知$\angle ACB = \angle DFE$,又$\angle ACB = 30^{\circ}$,$\therefore \angle DFE = 30^{\circ}$.$\therefore$ 在$Rt\triangle FEP$中,$EP = \frac{1}{2}EF = 3$,即点$E$到$BC$的距离为$3$(也可以用全等三角形对应边上的高相等)
17. $\triangle ABD$是等边三角形.证明:$\because AE$的垂直平分线交$BE$于点$C$,$\therefore CA = CE$.$\therefore \angle CAE = \angle E = 15^{\circ}$.$\therefore \angle ACB = \angle CAE + \angle E = 30^{\circ}$.$\therefore$ 在$Rt\triangle ABC$中,$\angle BAC = 60^{\circ}$.$\because$ 在$Rt\triangle ABC$中,$D$为$AC$的中点,$\therefore DA = DB$.$\therefore \triangle ABD$是等边三角形
18. 在$\triangle APD$中,$AD + AP > PD$,$\because PQ = AD$,$\therefore PQ + AP > PD$即$AQ > PD$.$\because$ 点$Q$在$\triangle ABC$的边上,$\therefore \angle ACQ < 60^{\circ}$.$\because \angle A = 60^{\circ}$,$\therefore \angle A > \angle ACQ$.$\therefore CQ > AQ$,$\therefore CQ > PD$
19. $\because AX\perp AC$,$\therefore \angle C = \angle QAP = 90^{\circ}$.$\therefore$ 点$C$与点$A$是对应点.$\therefore$ 当$\triangle CAB\cong\triangle APQ$时,则$AP = CA = 10$,即$P$,$C$两点重合.$\therefore$ 当$\triangle CAB\cong\triangle AQP$时,则$AP = CB = 5$,即点$P$为$AC$中点.综上,当$\triangle ABC\cong\triangle APQ$时,点$P$与点$C$重合或为$AC$中点
20.
(1) 在$\triangle BDC$中,$BD = BC$,$\therefore \angle BDC = \angle BCD$.$\because \angle ABC = 80^{\circ}$,$\therefore \angle BDC = 50^{\circ}$.在$\triangle ABC$中,$\angle ABC = 80^{\circ}$,$\angle A = 40^{\circ}$,则$\angle ACB = 60^{\circ}$.$\because CE = CB$,$\therefore \triangle BCE$是等边三角形.$\therefore \angle BEC = 60^{\circ}$.$\because \angle BEC$是$\triangle ABE$的外角,$\therefore \angle ABE = \angle BEC - \angle A = 60^{\circ} - 40^{\circ} = 20^{\circ}$
(2) $\angle BDC + \angle BEC = 110^{\circ}$.理由:设$\angle ABC = \alpha^{\circ}$,在$\triangle BDC$中,$BD = BC$,则$\angle BDC = \frac{1}{2}(180 - \alpha)^{\circ}$.在$\triangle ABC$中,$\angle ACB = 180^{\circ} - 40^{\circ} - \alpha^{\circ} = (140 - \alpha)^{\circ}$.在$\triangle BEC$中,$CE = CB$,则$\angle BEC = \frac{1}{2}(180 - 140 + \alpha)^{\circ} = \frac{1}{2}(40 + \alpha)^{\circ}$.$\therefore \angle BDC + \angle BEC = \frac{1}{2}(180 - \alpha)^{\circ} + \frac{1}{2}(40 + \alpha)^{\circ} = 110^{\circ}$
21.
(1) $\because \angle ABC$,$\angle ACB$的平分线相交于点$M$,$\therefore \angle MBC = \frac{1}{2}\angle ABC$,$\angle MCB = \frac{1}{2}\angle ACB$.$\therefore \angle MBC + \angle MCB = \frac{1}{2}(\angle ABC + \angle ACB)$.在$\triangle ABC$中,$\angle A = 70^{\circ}$,则$\angle ABC + \angle ACB = 180^{\circ} - 70^{\circ} = 110^{\circ}$,$\therefore \angle MBC + \angle MCB = 55^{\circ}$.$\therefore \angle BMC = 125^{\circ}$
(2) $\because \angle ABC$,$\angle ACB$的平分线相交于点$M$,$\therefore \angle MBC = \angle DBM$,$\angle MCB = \angle ECM$.$\therefore DM = DB$,$EM = EC$.$\therefore \triangle ADE$的周长$ = AD + DE + AE = AB + AC = \triangle ABC$的周长$- BC = m - a$
22.
(1) 如图所示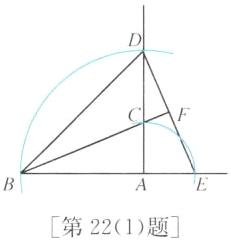
(2) $\because \triangle ADE$是$\triangle ABC$绕顶点$A$按顺时针方向旋转$90^{\circ}$得到的,$\therefore \triangle ADE\cong\triangle ABC$.$\therefore \angle ABC = \angle ADE$,$BC = DE$,$AB = AD$.$\because \angle ADE + \angle DEA = 90^{\circ}$,$\therefore \angle ABC + \angle DEA = 90^{\circ}$.$\therefore BF\perp DE$.又$BC = 2EF$,$DE = 2EF$,即$BF$垂直平分$DE$,$\therefore BD = BE$,即$\triangle BDE$是等腰三角形.$\because AB = AD$,$\angle BAD = 90^{\circ}$,$\therefore$ 在等腰直角三角形$BDA$中,$\angle ABD = \angle BDA = 45^{\circ}$.$\because BD = BE$,$\therefore \angle BDE = \frac{1}{2}(180^{\circ} - 45^{\circ}) = 67.5^{\circ}$.$\therefore \angle ABC = 67.5^{\circ} - 45^{\circ} = 22.5^{\circ}$
16.
(1) $\because AB// DE$,$\therefore \angle A = \angle D$.同理$\angle ACB = \angle DFE$.$\because BF = DC$,$\therefore BF + FC = DC + FC$,即$BC = DF$.$\therefore \triangle ABC\cong \triangle EDF$
(2) 作$EP\perp BD$,垂足为点$P$,$\because \triangle ABC\cong \triangle EDF$,$\therefore EF = AC = 6$.由
(1)知$\angle ACB = \angle DFE$,又$\angle ACB = 30^{\circ}$,$\therefore \angle DFE = 30^{\circ}$.$\therefore$ 在$Rt\triangle FEP$中,$EP = \frac{1}{2}EF = 3$,即点$E$到$BC$的距离为$3$(也可以用全等三角形对应边上的高相等)
17. $\triangle ABD$是等边三角形.证明:$\because AE$的垂直平分线交$BE$于点$C$,$\therefore CA = CE$.$\therefore \angle CAE = \angle E = 15^{\circ}$.$\therefore \angle ACB = \angle CAE + \angle E = 30^{\circ}$.$\therefore$ 在$Rt\triangle ABC$中,$\angle BAC = 60^{\circ}$.$\because$ 在$Rt\triangle ABC$中,$D$为$AC$的中点,$\therefore DA = DB$.$\therefore \triangle ABD$是等边三角形
18. 在$\triangle APD$中,$AD + AP > PD$,$\because PQ = AD$,$\therefore PQ + AP > PD$即$AQ > PD$.$\because$ 点$Q$在$\triangle ABC$的边上,$\therefore \angle ACQ < 60^{\circ}$.$\because \angle A = 60^{\circ}$,$\therefore \angle A > \angle ACQ$.$\therefore CQ > AQ$,$\therefore CQ > PD$
19. $\because AX\perp AC$,$\therefore \angle C = \angle QAP = 90^{\circ}$.$\therefore$ 点$C$与点$A$是对应点.$\therefore$ 当$\triangle CAB\cong\triangle APQ$时,则$AP = CA = 10$,即$P$,$C$两点重合.$\therefore$ 当$\triangle CAB\cong\triangle AQP$时,则$AP = CB = 5$,即点$P$为$AC$中点.综上,当$\triangle ABC\cong\triangle APQ$时,点$P$与点$C$重合或为$AC$中点
20.
(1) 在$\triangle BDC$中,$BD = BC$,$\therefore \angle BDC = \angle BCD$.$\because \angle ABC = 80^{\circ}$,$\therefore \angle BDC = 50^{\circ}$.在$\triangle ABC$中,$\angle ABC = 80^{\circ}$,$\angle A = 40^{\circ}$,则$\angle ACB = 60^{\circ}$.$\because CE = CB$,$\therefore \triangle BCE$是等边三角形.$\therefore \angle BEC = 60^{\circ}$.$\because \angle BEC$是$\triangle ABE$的外角,$\therefore \angle ABE = \angle BEC - \angle A = 60^{\circ} - 40^{\circ} = 20^{\circ}$
(2) $\angle BDC + \angle BEC = 110^{\circ}$.理由:设$\angle ABC = \alpha^{\circ}$,在$\triangle BDC$中,$BD = BC$,则$\angle BDC = \frac{1}{2}(180 - \alpha)^{\circ}$.在$\triangle ABC$中,$\angle ACB = 180^{\circ} - 40^{\circ} - \alpha^{\circ} = (140 - \alpha)^{\circ}$.在$\triangle BEC$中,$CE = CB$,则$\angle BEC = \frac{1}{2}(180 - 140 + \alpha)^{\circ} = \frac{1}{2}(40 + \alpha)^{\circ}$.$\therefore \angle BDC + \angle BEC = \frac{1}{2}(180 - \alpha)^{\circ} + \frac{1}{2}(40 + \alpha)^{\circ} = 110^{\circ}$
21.
(1) $\because \angle ABC$,$\angle ACB$的平分线相交于点$M$,$\therefore \angle MBC = \frac{1}{2}\angle ABC$,$\angle MCB = \frac{1}{2}\angle ACB$.$\therefore \angle MBC + \angle MCB = \frac{1}{2}(\angle ABC + \angle ACB)$.在$\triangle ABC$中,$\angle A = 70^{\circ}$,则$\angle ABC + \angle ACB = 180^{\circ} - 70^{\circ} = 110^{\circ}$,$\therefore \angle MBC + \angle MCB = 55^{\circ}$.$\therefore \angle BMC = 125^{\circ}$
(2) $\because \angle ABC$,$\angle ACB$的平分线相交于点$M$,$\therefore \angle MBC = \angle DBM$,$\angle MCB = \angle ECM$.$\therefore DM = DB$,$EM = EC$.$\therefore \triangle ADE$的周长$ = AD + DE + AE = AB + AC = \triangle ABC$的周长$- BC = m - a$
22.
(1) 如图所示

(2) $\because \triangle ADE$是$\triangle ABC$绕顶点$A$按顺时针方向旋转$90^{\circ}$得到的,$\therefore \triangle ADE\cong\triangle ABC$.$\therefore \angle ABC = \angle ADE$,$BC = DE$,$AB = AD$.$\because \angle ADE + \angle DEA = 90^{\circ}$,$\therefore \angle ABC + \angle DEA = 90^{\circ}$.$\therefore BF\perp DE$.又$BC = 2EF$,$DE = 2EF$,即$BF$垂直平分$DE$,$\therefore BD = BE$,即$\triangle BDE$是等腰三角形.$\because AB = AD$,$\angle BAD = 90^{\circ}$,$\therefore$ 在等腰直角三角形$BDA$中,$\angle ABD = \angle BDA = 45^{\circ}$.$\because BD = BE$,$\therefore \angle BDE = \frac{1}{2}(180^{\circ} - 45^{\circ}) = 67.5^{\circ}$.$\therefore \angle ABC = 67.5^{\circ} - 45^{\circ} = 22.5^{\circ}$