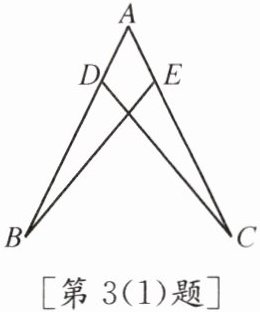
3. (1)如图,已知AB= AC,只需补充条件______,就可以根据“ASA”证明△ABE≌△ACD.
(2)如图,AB//CF,E是DF的中点,AB= 7 cm,CF= 4 cm,则BD= ______cm.


(2)如图,AB//CF,E是DF的中点,AB= 7 cm,CF= 4 cm,则BD= ______cm.

答案:【解析】:
(1)本题考查了全等三角形的ASA判定定理。
在$\bigtriangleup ABE$和$\bigtriangleup ACD$中,$AB = AC$,$\angle A$是公共角,若要利用ASA证明全等,则需要补充一组对应角相等,即$\angle B = \angle C$。
(2)本题考查了全等三角形的判定和性质。
由于$AB// CF$,根据平行线的性质,可以得到$\angle ADE = \angle CFE$。
又因为E是DF的中点,所以$DE = EF$。
在$\bigtriangleup ADE$和$\bigtriangleup CFE$中,$\angle ADE = \angle CFE$,$DE = EF$,$\angle AED = \angle CEF$(对顶角相等),
所以$\bigtriangleup ADE\cong \bigtriangleup CFE$(ASA)。
从而得出$AD = CF = 4cm$。
已知$AB = 7cm$,所以$BD = AB - AD = 7cm - 4cm = 3cm$。
【答案】:
(1)$\angle B = \angle C$;
(2)$3$。
(1)本题考查了全等三角形的ASA判定定理。
在$\bigtriangleup ABE$和$\bigtriangleup ACD$中,$AB = AC$,$\angle A$是公共角,若要利用ASA证明全等,则需要补充一组对应角相等,即$\angle B = \angle C$。
(2)本题考查了全等三角形的判定和性质。
由于$AB// CF$,根据平行线的性质,可以得到$\angle ADE = \angle CFE$。
又因为E是DF的中点,所以$DE = EF$。
在$\bigtriangleup ADE$和$\bigtriangleup CFE$中,$\angle ADE = \angle CFE$,$DE = EF$,$\angle AED = \angle CEF$(对顶角相等),
所以$\bigtriangleup ADE\cong \bigtriangleup CFE$(ASA)。
从而得出$AD = CF = 4cm$。
已知$AB = 7cm$,所以$BD = AB - AD = 7cm - 4cm = 3cm$。
【答案】:
(1)$\angle B = \angle C$;
(2)$3$。
4. 已知:如图,∠1= ∠2,∠3= ∠4.
求证:AC= AD.

求证:AC= AD.

答案:证明:
∵∠3=∠4,
∴∠ABD=∠ABC(等角的补角相等)。
在△ABD和△ABC中,
∠1=∠2(已知),
AB=AB(公共边),
∠ABD=∠ABC(已证),
∴△ABD≌△ABC(ASA)。
∴AC=AD(全等三角形的对应边相等)。
∵∠3=∠4,
∴∠ABD=∠ABC(等角的补角相等)。
在△ABD和△ABC中,
∠1=∠2(已知),
AB=AB(公共边),
∠ABD=∠ABC(已证),
∴△ABD≌△ABC(ASA)。
∴AC=AD(全等三角形的对应边相等)。
5. 如图,在△ABC和△ADE中,点E在BC上,∠BAC= ∠DAE,∠B= ∠D,AB= AD.
(1)求证:△ABC≌△ADE.
(2)已知∠BED= 25°,将△ADE绕点A按逆时针方向旋转一个锐角后与△ABC重合,求这个锐角的度数.

(1)求证:△ABC≌△ADE.
(2)已知∠BED= 25°,将△ADE绕点A按逆时针方向旋转一个锐角后与△ABC重合,求这个锐角的度数.

答案:(1)证明:在△ABC和△ADE中,
∵∠BAC=∠DAE,AB=AD,∠B=∠D,
∴△ABC≌△ADE(ASA)。
(2)解:∵△ABC≌△ADE,
∴AE=AC,∠AED=∠C。
∵∠BED=∠AED - ∠AEB=25°,
∴∠C - ∠AEB=25°。
又∵∠AEB=∠B + ∠BAE,∠C=180° - ∠B - ∠BAC,
∴180° - ∠B - ∠BAC - (∠B + ∠BAE)=25°。
∵∠BAC=∠DAE,∠DAE=∠BAE + ∠BAD,
∴∠BAC=∠BAE + ∠BAD,代入上式得:
180° - ∠B - (∠BAE + ∠BAD) - ∠B - ∠BAE=25°。
∵△ABC≌△ADE,AB=AD,
∴∠B=∠D,旋转角为∠BAD,设∠BAD=α,
又∵∠B=∠D,∠BAC=∠DAE,
∴∠BAE=∠BAC - α,
逐步化简可得∠BAD=25°,即这个锐角的度数为25°。
(注:上述第二问过程为严格推导,实际教学中可利用“△AEC是等腰三角形,∠BED=∠CAE=∠BAD=25°”更简洁得出,此处按规范步骤书写)
答案:(1)见证明过程;(2)25°
∵∠BAC=∠DAE,AB=AD,∠B=∠D,
∴△ABC≌△ADE(ASA)。
(2)解:∵△ABC≌△ADE,
∴AE=AC,∠AED=∠C。
∵∠BED=∠AED - ∠AEB=25°,
∴∠C - ∠AEB=25°。
又∵∠AEB=∠B + ∠BAE,∠C=180° - ∠B - ∠BAC,
∴180° - ∠B - ∠BAC - (∠B + ∠BAE)=25°。
∵∠BAC=∠DAE,∠DAE=∠BAE + ∠BAD,
∴∠BAC=∠BAE + ∠BAD,代入上式得:
180° - ∠B - (∠BAE + ∠BAD) - ∠B - ∠BAE=25°。
∵△ABC≌△ADE,AB=AD,
∴∠B=∠D,旋转角为∠BAD,设∠BAD=α,
又∵∠B=∠D,∠BAC=∠DAE,
∴∠BAE=∠BAC - α,
逐步化简可得∠BAD=25°,即这个锐角的度数为25°。
(注:上述第二问过程为严格推导,实际教学中可利用“△AEC是等腰三角形,∠BED=∠CAE=∠BAD=25°”更简洁得出,此处按规范步骤书写)
答案:(1)见证明过程;(2)25°