画△ABC,使∠B= 40°,∠C= 60°,BC= 2 cm. 你画的三角形与其他同学画的三角形全等吗?
答案:解:画图步骤:
1. 画线段BC=2cm;
2. 以B为顶点,BC为一边,画∠B=40°;
3. 以C为顶点,CB为一边,画∠C=60°,两角的另一边交于点A;
4. 则△ABC即为所求。
根据“角边角”(ASA)判定定理,两角及其夹边分别相等的两个三角形全等,故所画三角形与其他同学画的三角形全等。
结论:全等。
1. 画线段BC=2cm;
2. 以B为顶点,BC为一边,画∠B=40°;
3. 以C为顶点,CB为一边,画∠C=60°,两角的另一边交于点A;
4. 则△ABC即为所求。
根据“角边角”(ASA)判定定理,两角及其夹边分别相等的两个三角形全等,故所画三角形与其他同学画的三角形全等。
结论:全等。
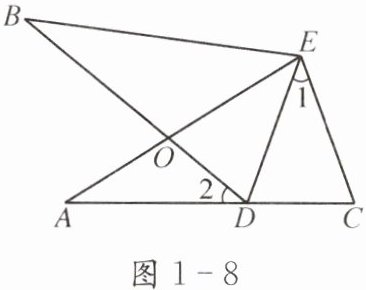
例 如图1-8,∠A= ∠B,AE= BE,点D在边AC上,∠1= ∠2,AE,BD相交于点O. 求证:△AEC≌△BED.

答案:证明:
∵∠A=∠B,∠AOD=∠BOE(对顶角相等),
∴∠2=∠BEO(三角形内角和定理)。
∵∠1=∠2,
∴∠1=∠BEO。
∵∠AEC=∠BEO+∠AEB,∠BED=∠1+∠AEB,
∴∠AEC=∠BED。
在△AEC和△BED中,
∠A=∠B,
AE=BE,
∠AEC=∠BED,
∴△AEC≌△BED(ASA)。
∵∠A=∠B,∠AOD=∠BOE(对顶角相等),
∴∠2=∠BEO(三角形内角和定理)。
∵∠1=∠2,
∴∠1=∠BEO。
∵∠AEC=∠BEO+∠AEB,∠BED=∠1+∠AEB,
∴∠AEC=∠BED。
在△AEC和△BED中,
∠A=∠B,
AE=BE,
∠AEC=∠BED,
∴△AEC≌△BED(ASA)。
1. 两角及其
如图,∵∠B= ∠B',BC=
夹边
分别相等的两个三角形全等(简写成角边角
或ASA
).如图,∵∠B= ∠B',BC=
B'C'
,∠C=∠C'
,∴△ABC≌△A'B'C'. (ASA
)答案:【解析】:
本题考查全等三角形的判定定理“角边角”(ASA)或“角角边”(AAS)。
对于第一个空,根据“角边角”定理,需要两角及其夹边分别相等,所以填“夹边”。
对于第二个空和第三个空,是“角边角”定理的简写,可写成“角边角”或“ASA”。
对于图中的填空,已知$\angle B = \angle B'$,根据“角边角”定理,还需要一对边相等和另一对角相等,从图中可知$BC = B'C'$,$\angle C = \angle C'$,最后根据“角边角”定理得出$\triangle ABC\cong\triangle A'B'C'$,判定定理为“ASA”。
【答案】:
夹边;角边角;ASA;$B'C'$;$\angle C'$;ASA
本题考查全等三角形的判定定理“角边角”(ASA)或“角角边”(AAS)。
对于第一个空,根据“角边角”定理,需要两角及其夹边分别相等,所以填“夹边”。
对于第二个空和第三个空,是“角边角”定理的简写,可写成“角边角”或“ASA”。
对于图中的填空,已知$\angle B = \angle B'$,根据“角边角”定理,还需要一对边相等和另一对角相等,从图中可知$BC = B'C'$,$\angle C = \angle C'$,最后根据“角边角”定理得出$\triangle ABC\cong\triangle A'B'C'$,判定定理为“ASA”。
【答案】:
夹边;角边角;ASA;$B'C'$;$\angle C'$;ASA
2. 选择题:
(1)小明将一块三角形纸板分割成如图所示的四块(图中标注为1,2,3,4). 若想用其中一块就能制作出与原来大小一样的三角形纸板,则应该选(
A. 第1块
B. 第2块
C. 第3块
D. 第4块

(2)如图,在△ABC中,∠CAD= ∠EAD,∠ADC= ∠ADE,CB= 5,BD= 3,则ED的长为(
A. 2
B. 3
C. 5
D. 8

(1)小明将一块三角形纸板分割成如图所示的四块(图中标注为1,2,3,4). 若想用其中一块就能制作出与原来大小一样的三角形纸板,则应该选(
B
).A. 第1块
B. 第2块
C. 第3块
D. 第4块

(2)如图,在△ABC中,∠CAD= ∠EAD,∠ADC= ∠ADE,CB= 5,BD= 3,则ED的长为(
A
).A. 2
B. 3
C. 5
D. 8

答案:(1)B;(2)A