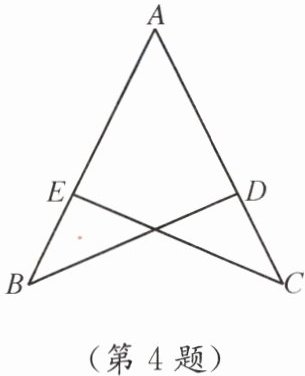
4. 如图,点D在AC上,点E在AB上,AB= AC,AD= AE.求证:△ABD≌△ACE.

答案:证明:在△ABD和△ACE中
$\begin{cases}AB=AC\\∠A=∠A(公共角)\\AD=AE\end{cases}$
∴△ABD≌△ACE(SAS)
$\begin{cases}AB=AC\\∠A=∠A(公共角)\\AD=AE\end{cases}$
∴△ABD≌△ACE(SAS)
5. 如图,点A,B,C在一条直线上,AD//BE,AD= BC,AB= BE.求证:BD= CE.


答案:【解析】:本题考查全等三角形的判定定理“边角边”,即两边及其夹角对应相等的两个三角形全等,全等三角形的对应边相等。要证明$BD = CE$,可通过证明$\triangle ABD$和$\triangle BEC$全等,利用全等三角形的性质得到对应边相等。
已知$AD// BE$,根据两直线平行,同位角相等,可得$\angle A = \angle EBC$。
又已知$AD = BC$,$AB = BE$,在$\triangle ABD$和$\triangle BEC$中,$AB = BE$,$\angle A = \angle EBC$,$AD = BC$,满足全等三角形判定定理“边角边”,所以$\triangle ABD\cong\triangle BEC(SAS)$。
因为全等三角形的对应边相等,$\triangle ABD\cong\triangle BEC$,所以$BD = CE$。
【答案】:证明:
∵$AD// BE$,
∴$\angle A = \angle EBC$。
在$\triangle ABD$和$\triangle BEC$中,
$\begin{cases}AB = BE \\ \angle A = \angle EBC \\ AD = BC\end{cases}$
∴$\triangle ABD\cong\triangle BEC(SAS)$。
∴$BD = CE$。
已知$AD// BE$,根据两直线平行,同位角相等,可得$\angle A = \angle EBC$。
又已知$AD = BC$,$AB = BE$,在$\triangle ABD$和$\triangle BEC$中,$AB = BE$,$\angle A = \angle EBC$,$AD = BC$,满足全等三角形判定定理“边角边”,所以$\triangle ABD\cong\triangle BEC(SAS)$。
因为全等三角形的对应边相等,$\triangle ABD\cong\triangle BEC$,所以$BD = CE$。
【答案】:证明:
∵$AD// BE$,
∴$\angle A = \angle EBC$。
在$\triangle ABD$和$\triangle BEC$中,
$\begin{cases}AB = BE \\ \angle A = \angle EBC \\ AD = BC\end{cases}$
∴$\triangle ABD\cong\triangle BEC(SAS)$。
∴$BD = CE$。
6. 如图,在等边三角形ABC中,D是BC延长线上的一点,连接AD,以AD为边作等边三角形ADE,连接CE.用学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.


答案:【解析】:本题可根据等边三角形的性质得出相关边和角的关系,再通过证明三角形全等,进而得出$AC$、$CD$、$CE$三条线段之间的数量关系。
已知$\triangle ABC$和$\triangle ADE$都是等边三角形,根据等边三角形的性质可知$AB = AC = BC$,$AD = AE$,$\angle BAC = \angle DAE = 60^{\circ}$。
因为$\angle BAC = \angle DAE$,所以$\angle BAC + \angle CAD = \angle DAE + \angle CAD$,即$\angle BAD = \angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD = \angle CAE$,$AD = AE$,根据全等三角形判定定理“边角边”($SAS$),可得$\triangle ABD\cong\triangle ACE$。
根据全等三角形的性质可知$BD = CE$,又因为$BD = BC + CD$,且$BC = AC$,所以$CE = AC + CD$。
【答案】:$CE = AC + CD$,探究过程如下:
证明:
∵$\triangle ABC$和$\triangle ADE$都是等边三角形,
∴$AB = AC = BC$,$AD = AE$,$\angle BAC = \angle DAE = 60^{\circ}$。
∴$\angle BAC + \angle CAD = \angle DAE + \angle CAD$,即$\angle BAD = \angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,
$\begin{cases}AB = AC\\\angle BAD = \angle CAE\\AD = AE\end{cases}$
∴$\triangle ABD\cong\triangle ACE(SAS)$。
∴$BD = CE$。
∵$BD = BC + CD$,$BC = AC$,
∴$CE = AC + CD$。
已知$\triangle ABC$和$\triangle ADE$都是等边三角形,根据等边三角形的性质可知$AB = AC = BC$,$AD = AE$,$\angle BAC = \angle DAE = 60^{\circ}$。
因为$\angle BAC = \angle DAE$,所以$\angle BAC + \angle CAD = \angle DAE + \angle CAD$,即$\angle BAD = \angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,$AB = AC$,$\angle BAD = \angle CAE$,$AD = AE$,根据全等三角形判定定理“边角边”($SAS$),可得$\triangle ABD\cong\triangle ACE$。
根据全等三角形的性质可知$BD = CE$,又因为$BD = BC + CD$,且$BC = AC$,所以$CE = AC + CD$。
【答案】:$CE = AC + CD$,探究过程如下:
证明:
∵$\triangle ABC$和$\triangle ADE$都是等边三角形,
∴$AB = AC = BC$,$AD = AE$,$\angle BAC = \angle DAE = 60^{\circ}$。
∴$\angle BAC + \angle CAD = \angle DAE + \angle CAD$,即$\angle BAD = \angle CAE$。
在$\triangle ABD$和$\triangle ACE$中,
$\begin{cases}AB = AC\\\angle BAD = \angle CAE\\AD = AE\end{cases}$
∴$\triangle ABD\cong\triangle ACE(SAS)$。
∴$BD = CE$。
∵$BD = BC + CD$,$BC = AC$,
∴$CE = AC + CD$。
7. 如图,△ABC≌△A'B'C',AD,A'D'分别是△ABC和△A'B'C'的中线.
(1)求证:AD= A'D'.
(2)用文字语言叙述第(1)题的结论.

(1)求证:AD= A'D'.
(2)用文字语言叙述第(1)题的结论.

答案:【解析】:
(1) 要证明两个中线相等,我们可以利用全等三角形的性质。已知△ABC≌△A'B'C',所以对应边相等,对应角相等。由于AD和A'D'分别是△ABC和△A'B'C'的中线,所以BD=B'D'(中线性质,中线将对边平分)。结合△ABC≌△A'B'C',我们可以得到△ABD≌△A'B'D'(SAS全等条件,即两边和夹角对应相等)。因此,对应边AD=A'D'。
(2) 用文字语言叙述第(1)题的结论就是:全等三角形的对应中线相等。
【答案】:
(1)证明:
∵△ABC≌△A'B'C',
∴AB=A'B',∠B=∠B',BC=B'C',
又∵AD,A'D'分别是△ABC和△A'B'C'的中线,
∴BD=$\frac{1}{2}$BC,B'D'=$\frac{1}{2}$B'C',
∴BD=B'D',
∵在△ABD和△A'B'D'中,
$\left\{\begin{array}{l}AB=A'B'\\\angle B=\angle B'\\BD=B'D'\end{array}\right.$
∴△ABD≌△A'B'D'(SAS),
∴AD=A'D'。
(2)解:
全等三角形的对应中线相等。
(1) 要证明两个中线相等,我们可以利用全等三角形的性质。已知△ABC≌△A'B'C',所以对应边相等,对应角相等。由于AD和A'D'分别是△ABC和△A'B'C'的中线,所以BD=B'D'(中线性质,中线将对边平分)。结合△ABC≌△A'B'C',我们可以得到△ABD≌△A'B'D'(SAS全等条件,即两边和夹角对应相等)。因此,对应边AD=A'D'。
(2) 用文字语言叙述第(1)题的结论就是:全等三角形的对应中线相等。
【答案】:
(1)证明:
∵△ABC≌△A'B'C',
∴AB=A'B',∠B=∠B',BC=B'C',
又∵AD,A'D'分别是△ABC和△A'B'C'的中线,
∴BD=$\frac{1}{2}$BC,B'D'=$\frac{1}{2}$B'C',
∴BD=B'D',
∵在△ABD和△A'B'D'中,
$\left\{\begin{array}{l}AB=A'B'\\\angle B=\angle B'\\BD=B'D'\end{array}\right.$
∴△ABD≌△A'B'D'(SAS),
∴AD=A'D'。
(2)解:
全等三角形的对应中线相等。