下列问题中,变量之间的对应关系是函数关系吗?如果是,写出函数表达式,这些函数表达式有哪些共同特征?
(1)圆的周长l随半径r的变化而变化;
(2)一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值h,再减常数105,所得差就是G的值;
(3)某城市的固定电话的月收费用y(单位:元)包括月租费22元和拨打电话x min的计时费(按0.1元/min收取);
(4)把一个长为10 cm、宽为5 cm的长方形的长减少x cm,宽不变,长方形的面积y(单位:$cm^2)$随x的变化而变化.
(1)圆的周长l随半径r的变化而变化;
(2)一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值h,再减常数105,所得差就是G的值;
(3)某城市的固定电话的月收费用y(单位:元)包括月租费22元和拨打电话x min的计时费(按0.1元/min收取);
(4)把一个长为10 cm、宽为5 cm的长方形的长减少x cm,宽不变,长方形的面积y(单位:$cm^2)$随x的变化而变化.
答案:(1)是函数关系,函数表达式为$l = 2\pi r$;
(2)是函数关系,函数表达式为$G = h - 105$;
(3)是函数关系,函数表达式为$y = 0.1x + 22$;
(4)是函数关系,函数表达式为$y = -5x + 50$($0 \leq x < 10$);
共同特征:这些函数表达式都是形如$y = kx + b$($k$、$b$是常数,$k \neq 0$)的形式。
(2)是函数关系,函数表达式为$G = h - 105$;
(3)是函数关系,函数表达式为$y = 0.1x + 22$;
(4)是函数关系,函数表达式为$y = -5x + 50$($0 \leq x < 10$);
共同特征:这些函数表达式都是形如$y = kx + b$($k$、$b$是常数,$k \neq 0$)的形式。
例 如图5-3,△ABC是边长为x的等边三角形.
(1)求边BC上的高h关于x的函数表达式,h是x的一次函数吗?如果是一次函数,写出相应的k和b的值.
(2)当h= $\sqrt{3}$时,求x的值.
(3)求△ABC的面积S关于x的函数表达式,S是x的一次函数吗?
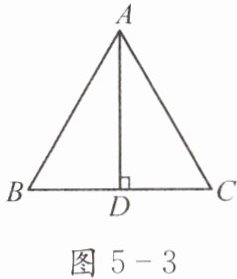
(1)求边BC上的高h关于x的函数表达式,h是x的一次函数吗?如果是一次函数,写出相应的k和b的值.
(2)当h= $\sqrt{3}$时,求x的值.
(3)求△ABC的面积S关于x的函数表达式,S是x的一次函数吗?

答案:【解析】:
(1)要求边$BC$上的高$h$关于$x$的函数表达式,需要利用等边三角形的性质,通过勾股定理求出高$h$与边长$x$的关系,再判断其是否为一次函数,并求出$k$和$b$的值。
(2)当$h = \sqrt{3}$时,将$h$的值代入(1)中求出的函数表达式,解方程求出$x$的值。
(3)要求$\triangle ABC$的面积$S$关于$x$的函数表达式,根据三角形面积公式$S=\frac{1}{2}×底×高$,结合(1)中求出的高$h$与$x$的关系,得出$S$与$x$的函数表达式,再判断其是否为一次函数。
【答案】:
(1)因为$\triangle ABC$是等边三角形,$AD\perp BC$,所以$D$为$BC$中点,$BD=\frac{1}{2}x$。
在$Rt\triangle ABD$中,根据勾股定理$AD^{2}=AB^{2}-BD^{2}$,已知$AB = x$,$BD=\frac{1}{2}x$,则$AD=\sqrt{x^{2}-(\frac{1}{2}x)^{2}}=\sqrt{\frac{3}{4}x^{2}}=\frac{\sqrt{3}}{2}x$,即$h = \frac{\sqrt{3}}{2}x$。
因为$h$是$x$的正比例函数(特殊的一次函数),属于一次函数,其中$k = \frac{\sqrt{3}}{2}$,$b = 0$。
(2)当$h = \sqrt{3}$时,代入$h = \frac{\sqrt{3}}{2}x$,可得$\sqrt{3}=\frac{\sqrt{3}}{2}x$,解得$x = 2$。
(3)根据三角形面积公式$S=\frac{1}{2}× BC× h$,已知$BC = x$,$h = \frac{\sqrt{3}}{2}x$,则$S=\frac{1}{2}× x×\frac{\sqrt{3}}{2}x=\frac{\sqrt{3}}{4}x^{2}$。
因为$S$是$x$的二次函数,所以$S$不是$x$的一次函数。
综上,答案依次为:(1)$h = \frac{\sqrt{3}}{2}x$,是一次函数,$k = \frac{\sqrt{3}}{2}$,$b = 0$;(2)$x = 2$;(3)$S=\frac{\sqrt{3}}{4}x^{2}$,$S$不是$x$的一次函数。
(1)要求边$BC$上的高$h$关于$x$的函数表达式,需要利用等边三角形的性质,通过勾股定理求出高$h$与边长$x$的关系,再判断其是否为一次函数,并求出$k$和$b$的值。
(2)当$h = \sqrt{3}$时,将$h$的值代入(1)中求出的函数表达式,解方程求出$x$的值。
(3)要求$\triangle ABC$的面积$S$关于$x$的函数表达式,根据三角形面积公式$S=\frac{1}{2}×底×高$,结合(1)中求出的高$h$与$x$的关系,得出$S$与$x$的函数表达式,再判断其是否为一次函数。
【答案】:
(1)因为$\triangle ABC$是等边三角形,$AD\perp BC$,所以$D$为$BC$中点,$BD=\frac{1}{2}x$。
在$Rt\triangle ABD$中,根据勾股定理$AD^{2}=AB^{2}-BD^{2}$,已知$AB = x$,$BD=\frac{1}{2}x$,则$AD=\sqrt{x^{2}-(\frac{1}{2}x)^{2}}=\sqrt{\frac{3}{4}x^{2}}=\frac{\sqrt{3}}{2}x$,即$h = \frac{\sqrt{3}}{2}x$。
因为$h$是$x$的正比例函数(特殊的一次函数),属于一次函数,其中$k = \frac{\sqrt{3}}{2}$,$b = 0$。
(2)当$h = \sqrt{3}$时,代入$h = \frac{\sqrt{3}}{2}x$,可得$\sqrt{3}=\frac{\sqrt{3}}{2}x$,解得$x = 2$。
(3)根据三角形面积公式$S=\frac{1}{2}× BC× h$,已知$BC = x$,$h = \frac{\sqrt{3}}{2}x$,则$S=\frac{1}{2}× x×\frac{\sqrt{3}}{2}x=\frac{\sqrt{3}}{4}x^{2}$。
因为$S$是$x$的二次函数,所以$S$不是$x$的一次函数。
综上,答案依次为:(1)$h = \frac{\sqrt{3}}{2}x$,是一次函数,$k = \frac{\sqrt{3}}{2}$,$b = 0$;(2)$x = 2$;(3)$S=\frac{\sqrt{3}}{4}x^{2}$,$S$不是$x$的一次函数。
1. 选择题:
(1)下列函数:①y= πx;②y= 2x-1;③y= $\frac{1}{x}$;④y= 2-3x;⑤y= x^2-1.其中,是一次函数的有(
A. 4个
B. 3个
C. 2个
D. 1个
(2)下列函数中,正比例函数是(
A. y= 3x-1
B. y= -3x
C. y= 5x^2
D. y= $\frac{2}{x}$
(1)下列函数:①y= πx;②y= 2x-1;③y= $\frac{1}{x}$;④y= 2-3x;⑤y= x^2-1.其中,是一次函数的有(
B
).A. 4个
B. 3个
C. 2个
D. 1个
(2)下列函数中,正比例函数是(
B
).A. y= 3x-1
B. y= -3x
C. y= 5x^2
D. y= $\frac{2}{x}$
答案:【解析】:
本题考查了一次函数和正比例函数的概念。
对于第一问,我们需要先明确一次函数的定义,一次函数是形如$y=kx+b$(其中$k$和$b$为常数,$k \neq 0$)的函数。
然后我们对题目中的各个函数进行逐一判断:
①$y= \pi x$,可以看作是$y=kx$的形式,其中$k=\pi$,$b=0$,所以是一次函数。
②$y= 2x-1$,可以看作是$y=kx+b$的形式,其中$k=2$,$b=-1$,所以是一次函数。
③$y= \frac{1}{x}$,此函数的形式并非$y=kx+b$,所以不是一次函数。
④$y= 2-3x$,可以看作是$y=kx+b$的形式,其中$k=-3$,$b=2$,所以是一次函数。
⑤$y= x^2-1$,此函数的形式并非$y=kx+b$,因为含有$x^2$项,所以不是一次函数。
综上,是一次函数的有3个,所以第一问的答案是B。
对于第二问,我们需要明确正比例函数的定义,正比例函数是形如$y=kx$(其中$k$为常数,$k \neq 0$)的函数,即一次函数中$b=0$的特殊情况。
然后我们对题目中的各个函数进行逐一判断:
A. $y= 3x-1$,因为$b \neq 0$,所以不是正比例函数。
B. $y= -3x$,可以看作是$y=kx$的形式,其中$k=-3$,所以是正比例函数。
C. $y= 5x^2$,此函数的形式并非$y=kx$,所以不是正比例函数。
D. $y= \frac{2}{x}$,此函数的形式并非$y=kx$,所以不是正比例函数。
综上,正比例函数是B,所以第二问的答案也是B。
【答案】:
(1)B;(2)B
本题考查了一次函数和正比例函数的概念。
对于第一问,我们需要先明确一次函数的定义,一次函数是形如$y=kx+b$(其中$k$和$b$为常数,$k \neq 0$)的函数。
然后我们对题目中的各个函数进行逐一判断:
①$y= \pi x$,可以看作是$y=kx$的形式,其中$k=\pi$,$b=0$,所以是一次函数。
②$y= 2x-1$,可以看作是$y=kx+b$的形式,其中$k=2$,$b=-1$,所以是一次函数。
③$y= \frac{1}{x}$,此函数的形式并非$y=kx+b$,所以不是一次函数。
④$y= 2-3x$,可以看作是$y=kx+b$的形式,其中$k=-3$,$b=2$,所以是一次函数。
⑤$y= x^2-1$,此函数的形式并非$y=kx+b$,因为含有$x^2$项,所以不是一次函数。
综上,是一次函数的有3个,所以第一问的答案是B。
对于第二问,我们需要明确正比例函数的定义,正比例函数是形如$y=kx$(其中$k$为常数,$k \neq 0$)的函数,即一次函数中$b=0$的特殊情况。
然后我们对题目中的各个函数进行逐一判断:
A. $y= 3x-1$,因为$b \neq 0$,所以不是正比例函数。
B. $y= -3x$,可以看作是$y=kx$的形式,其中$k=-3$,所以是正比例函数。
C. $y= 5x^2$,此函数的形式并非$y=kx$,所以不是正比例函数。
D. $y= \frac{2}{x}$,此函数的形式并非$y=kx$,所以不是正比例函数。
综上,正比例函数是B,所以第二问的答案也是B。
【答案】:
(1)B;(2)B