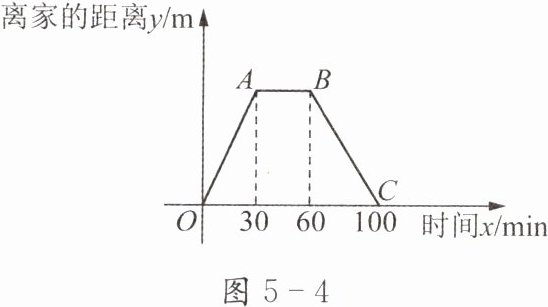
图5-4描述了某一天小亮从家骑车去书店购书,然后骑车回家的情况.你能说出小亮在路上的情形吗?

答案:【解析】:本题考查对一次函数图像的理解,通过分析图像中横纵坐标的含义以及函数的变化趋势,来描述小亮在路上的情形,包括出发时间、到达书店时间、在书店停留时间、回家时间等关键信息。
从图像中可以看出:
小亮从家出发,随着时间的增加,离家的距离逐渐增大,在$30$分钟时到达书店,此时离家的距离达到最大值,说明小亮在$30$分钟内骑车到达了书店。
从$30$分钟到$60$分钟,离家的距离没有变化,说明小亮在书店停留了$60 - 30 = 30$分钟。
$60$分钟之后,离家的距离逐渐减小,说明小亮开始骑车回家,在$100$分钟时离家的距离为$0$,说明小亮在$100 - 60 = 40$分钟内骑车回到了家。
【答案】:小亮从家出发,$30$分钟到达书店,在书店停留$30$分钟,然后$40$分钟回到家。
从图像中可以看出:
小亮从家出发,随着时间的增加,离家的距离逐渐增大,在$30$分钟时到达书店,此时离家的距离达到最大值,说明小亮在$30$分钟内骑车到达了书店。
从$30$分钟到$60$分钟,离家的距离没有变化,说明小亮在书店停留了$60 - 30 = 30$分钟。
$60$分钟之后,离家的距离逐渐减小,说明小亮开始骑车回家,在$100$分钟时离家的距离为$0$,说明小亮在$100 - 60 = 40$分钟内骑车回到了家。
【答案】:小亮从家出发,$30$分钟到达书店,在书店停留$30$分钟,然后$40$分钟回到家。
例 甲骑自行车以10 km/h的速度沿公路骑行,出发3 h后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25 km/h.
(1)设甲离开出发地的时间为x h.
① 求甲离开出发地的路程y km关于x h的函数表达式,并指出自变量x的取值范围;
② 求乙离开出发地的路程y km关于x h的函数表达式,并指出自变量x的取值范围.
(2)在同一平面直角坐标系中,画出(1)中两个函数的图象,并结合实际问题,解释图象中交点的意义.
(1)设甲离开出发地的时间为x h.
① 求甲离开出发地的路程y km关于x h的函数表达式,并指出自变量x的取值范围;
② 求乙离开出发地的路程y km关于x h的函数表达式,并指出自变量x的取值范围.
(2)在同一平面直角坐标系中,画出(1)中两个函数的图象,并结合实际问题,解释图象中交点的意义.
答案:【解析】:
本题主要考查一次函数的应用,包括函数的建立、自变量取值范围的确定、函数图像的绘制以及图像交点意义的解释。
(1) ① 对于甲,其速度是10 km/h,时间是x h,所以其离开出发地的路程是速度乘以时间,即$y = 10x$。
由于甲从出发开始就一直骑行,所以时间x的取值范围是从0开始,即$x \geq 0$。
② 对于乙,其速度是25 km/h,但乙比甲晚出发3 h,所以乙骑行的时间是$x - 3$ h。
因此,乙离开出发地的路程是$y = 25(x - 3)$,但需要注意,这个表达式只在乙出发后有效,即$x \geq 3$。
同时,由于题目没有给出乙骑行的总时间,我们可以默认乙一直在骑行,所以x的取值范围是$x \geq 3$。
(2) 对于函数图像的绘制,我们可以根据上面得到的函数表达式,在平面直角坐标系中绘制出两条直线。
图像的交点表示在同一时间点,甲和乙离开出发地的路程相同,即他们相遇了。
【答案】:
(1) ① $y = 10x$,$x \geq 0$;
② $y = 25(x - 3)$,$x \geq 3$;
(2) 图略;交点的意义:表示在同一时间点,甲和乙离开出发地的路程相同,即他们相遇了。
本题主要考查一次函数的应用,包括函数的建立、自变量取值范围的确定、函数图像的绘制以及图像交点意义的解释。
(1) ① 对于甲,其速度是10 km/h,时间是x h,所以其离开出发地的路程是速度乘以时间,即$y = 10x$。
由于甲从出发开始就一直骑行,所以时间x的取值范围是从0开始,即$x \geq 0$。
② 对于乙,其速度是25 km/h,但乙比甲晚出发3 h,所以乙骑行的时间是$x - 3$ h。
因此,乙离开出发地的路程是$y = 25(x - 3)$,但需要注意,这个表达式只在乙出发后有效,即$x \geq 3$。
同时,由于题目没有给出乙骑行的总时间,我们可以默认乙一直在骑行,所以x的取值范围是$x \geq 3$。
(2) 对于函数图像的绘制,我们可以根据上面得到的函数表达式,在平面直角坐标系中绘制出两条直线。
图像的交点表示在同一时间点,甲和乙离开出发地的路程相同,即他们相遇了。
【答案】:
(1) ① $y = 10x$,$x \geq 0$;
② $y = 25(x - 3)$,$x \geq 3$;
(2) 图略;交点的意义:表示在同一时间点,甲和乙离开出发地的路程相同,即他们相遇了。
1. 如图是某长途汽车客运站旅客携带行李费用示意图.免费行李的质量不超过
40
kg,超过此质量,行李费用y元关于行李质量x kg的函数表达式为y = x - 40(x > 40)
.答案:【解析】:
本题主要考查一次函数的应用。
首先,观察图示,当行李质量不超过$40kg$时,费用为$0$元。
因此,免费行李的质量上限是$40kg$。
其次,当行李质量超过$40kg$时,费用开始产生,并且呈线性增长。
设超过$40kg$后,每增加$1kg$行李,费用增加$k$元。
那么,当行李质量为$x kg(x > 40)$时,超出的质量为$(x - 40)kg$,
所需支付的额外费用就是$k(x - 40)$元。
由图示可知,当$x = 50$时,$y = 10$,
代入上式得:$10 = k(50 - 40)$,
解得:$k = 1$。
因此,当$x > 40$时,行李费用$y$关于行李质量$x$的函数表达式为$y = x - 40$。
【答案】:
$40$;$y = x - 40(x > 40)$。
本题主要考查一次函数的应用。
首先,观察图示,当行李质量不超过$40kg$时,费用为$0$元。
因此,免费行李的质量上限是$40kg$。
其次,当行李质量超过$40kg$时,费用开始产生,并且呈线性增长。
设超过$40kg$后,每增加$1kg$行李,费用增加$k$元。
那么,当行李质量为$x kg(x > 40)$时,超出的质量为$(x - 40)kg$,
所需支付的额外费用就是$k(x - 40)$元。
由图示可知,当$x = 50$时,$y = 10$,
代入上式得:$10 = k(50 - 40)$,
解得:$k = 1$。
因此,当$x > 40$时,行李费用$y$关于行李质量$x$的函数表达式为$y = x - 40$。
【答案】:
$40$;$y = x - 40(x > 40)$。
2. 如图,一长为50 cm,宽为20 cm的长方形木板,现要在长边上截去长为x cm的一部分,则剩余木板的面积$S cm^2$关于x cm(0≤x<50)的表达式为(
A.S= 1000-x
B.S= 1000-20x
C.S= 20x
D.S= 50x
B
).A.S= 1000-x
B.S= 1000-20x
C.S= 20x
D.S= 50x
答案:【解析】:本题主要考查了一次函数的实际应用。
长方形的面积公式为:$面积 = 长 × 宽$。
原始木板的长为$50cm$,宽为$20cm$,所以原始面积为:
$S_{原始} = 50 × 20 = 1000 cm^2$,
在长边上截去长为$x cm$的一部分后,剩余的长为$(50 - x) cm$,宽仍为$20 cm$。
但更方便的方法是直接考虑截去部分的面积,然后用原始面积减去截去部分的面积。
截去部分的面积为:
$S_{截去} = x × 20= 20x cm^2$,
所以,剩余木板的面积为:
$S = S_{原始} - S_{截去}= 1000 - 20x cm^2$,
根据以上分析,答案为B。
【答案】:B。
长方形的面积公式为:$面积 = 长 × 宽$。
原始木板的长为$50cm$,宽为$20cm$,所以原始面积为:
$S_{原始} = 50 × 20 = 1000 cm^2$,
在长边上截去长为$x cm$的一部分后,剩余的长为$(50 - x) cm$,宽仍为$20 cm$。
但更方便的方法是直接考虑截去部分的面积,然后用原始面积减去截去部分的面积。
截去部分的面积为:
$S_{截去} = x × 20= 20x cm^2$,
所以,剩余木板的面积为:
$S = S_{原始} - S_{截去}= 1000 - 20x cm^2$,
根据以上分析,答案为B。
【答案】:B。