3. 某种子商店销售一种小麦种子,为促销,制订了两种销售方案供采购者选择.
方案一:小麦种子的价格为4元/kg,无论购买多少均不打折.
方案二:购买3 kg以内(含3 kg),价格为5元/kg;若一次性购买超过3 kg,则超过3 kg的部分种子价格打7折.
(1)求出方案一中购买的小麦种子的付款金额y关于数量x的函数表达式.
(2)若购买一定量的小麦种子,你会选择哪种方案?说明理由.
方案一:小麦种子的价格为4元/kg,无论购买多少均不打折.
方案二:购买3 kg以内(含3 kg),价格为5元/kg;若一次性购买超过3 kg,则超过3 kg的部分种子价格打7折.
(1)求出方案一中购买的小麦种子的付款金额y关于数量x的函数表达式.
(2)若购买一定量的小麦种子,你会选择哪种方案?说明理由.
答案:【解析】:
本题主要考查一次函数的应用,需要根据题目条件设立函数模型,并通过比较函数值来做出最优选择。
(1) 对于方案一,由于价格固定为4元/kg,不受购买数量的影响,所以付款金额$y$与购买数量$x$的关系是线性的,即$y = 4x$。
(2) 对于方案二,需要分两种情况考虑:
当$0 \lt x \leq 3$时,价格为5元/kg,所以$y = 5x$;
当$x \gt 3$时,前3kg的价格是$3 × 5 = 15$元,超过3kg的部分打7折,即每千克$5 × 0.7 = 3.5$元,
所以$y = 15 + 3.5(x - 3) = 3.5x + 4.5$。
接下来,我们需要比较两种方案的花费,以确定哪种方案更优惠。
设两种方案的花费相等,即$4x = 3.5x + 4.5$,
移项得:$4x - 3.5x = 4.5$,
合并同类项得:$0.5x = 4.5$,
系数化为$1$得:$x = 9$。
这是两种方案花费相同的购买量。
当购买量$x \lt 9$时,方案一的花费$4x$会小于方案二的花费$3.5x + 4.5$;
当购买量$x \gt 9$时,方案一的花费$4x$会大于方案二的花费$3.5x + 4.5$。
【答案】:
(1) 方案一中购买的小麦种子的付款金额$y$关于数量$x$的函数表达式为$y = 4x$;
(2) 当购买小麦种子的数量$x \lt 9$时,选择方案一更合算;
当购买小麦种子的数量$x = 9$时,两种方案一样;
当购买小麦种子的数量$x \gt 9$时,选择方案二更合算。
本题主要考查一次函数的应用,需要根据题目条件设立函数模型,并通过比较函数值来做出最优选择。
(1) 对于方案一,由于价格固定为4元/kg,不受购买数量的影响,所以付款金额$y$与购买数量$x$的关系是线性的,即$y = 4x$。
(2) 对于方案二,需要分两种情况考虑:
当$0 \lt x \leq 3$时,价格为5元/kg,所以$y = 5x$;
当$x \gt 3$时,前3kg的价格是$3 × 5 = 15$元,超过3kg的部分打7折,即每千克$5 × 0.7 = 3.5$元,
所以$y = 15 + 3.5(x - 3) = 3.5x + 4.5$。
接下来,我们需要比较两种方案的花费,以确定哪种方案更优惠。
设两种方案的花费相等,即$4x = 3.5x + 4.5$,
移项得:$4x - 3.5x = 4.5$,
合并同类项得:$0.5x = 4.5$,
系数化为$1$得:$x = 9$。
这是两种方案花费相同的购买量。
当购买量$x \lt 9$时,方案一的花费$4x$会小于方案二的花费$3.5x + 4.5$;
当购买量$x \gt 9$时,方案一的花费$4x$会大于方案二的花费$3.5x + 4.5$。
【答案】:
(1) 方案一中购买的小麦种子的付款金额$y$关于数量$x$的函数表达式为$y = 4x$;
(2) 当购买小麦种子的数量$x \lt 9$时,选择方案一更合算;
当购买小麦种子的数量$x = 9$时,两种方案一样;
当购买小麦种子的数量$x \gt 9$时,选择方案二更合算。
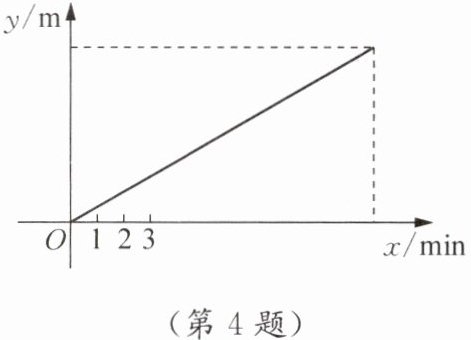
4. 甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离$y_1 m$关于时间x min的函数关系如图所示.
(1)在图中画出乙离A地的距离$y_2 m$关于时间x min的函数图象;
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
(1)在图中画出乙离A地的距离$y_2 m$关于时间x min的函数图象;
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.

答案:答案略
解析:
(1)图略(过点$(1,0)$且斜率为甲的2倍的射线)
(2)设甲整个行程所用的时间为$t$ min,甲的速度为$v$ m/min,则乙的速度为$2v$ m/min。
甲走完全程的距离为$vt$ m。
乙比甲晚出发1 min,且甲比乙晚5 min到达,所以乙走完全程所用时间为$(t - 1 - 5)$min = $(t - 6)$min。
乙走完全程的距离为$2v(t - 6)$ m。
因为甲、乙走的是同一段路程,所以$vt=2v(t - 6)$,解得$t = 12$。
答:甲整个行程所用的时间为12 min。
(2)设甲整个行程所用的时间为$t$ min,甲的速度为$v$ m/min,则乙的速度为$2v$ m/min。
甲走完全程的距离为$vt$ m。
乙比甲晚出发1 min,且甲比乙晚5 min到达,所以乙走完全程所用时间为$(t - 1 - 5)$min = $(t - 6)$min。
乙走完全程的距离为$2v(t - 6)$ m。
因为甲、乙走的是同一段路程,所以$vt=2v(t - 6)$,解得$t = 12$。
答:甲整个行程所用的时间为12 min。
5. (1)如图可以反映一个实际情境:一艘船从甲地航行到乙地,到达乙地后立即返回.这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离.这艘船从甲地到乙地航行的速度与返航的速度是否相同?说明理由.
(2)给该图赋予一个新的实际背景,提出一个具体问题.指出实际背景中横坐标、纵坐标所表示的意思,写出A,B两点的坐标,解决所提出的实际问题.

(2)给该图赋予一个新的实际背景,提出一个具体问题.指出实际背景中横坐标、纵坐标所表示的意思,写出A,B两点的坐标,解决所提出的实际问题.

答案:【解析】:本题主要考查了一次函数在实际情境中的应用,通过函数图象来分析船的航行速度以及赋予新的实际背景解决问题。对于(1),需要根据路程、时间和速度的关系,结合图象中从甲地到乙地以及返航所用的时间来判断速度是否相同;对于(2),需要发挥想象力,赋予图象合理的实际背景,并根据背景确定横坐标、纵坐标的意义,求出$A$、$B$两点坐标并解决问题。
(1)从图象可知,船从甲地到乙地航行和返航的路程相同,设为$s$。
从甲地到乙地航行所用的时间为$t_1$,返航所用的时间为$t_2$。
根据速度公式$v = \frac{s}{t}$,从图象横坐标可以看出,从甲地到乙地航行对应的时间间隔较小,返航对应的时间间隔较大,即$t_1\lt t_2$。
因为路程$s$相同,根据$v = \frac{s}{t}$,当$s$一定时,$t$越大,$v$越小,所以船从甲地到乙地航行的速度与返航的速度不相同,从甲地到乙地航行的速度大于返航的速度。
(2)新实际背景:小明从家出发去学校,到达学校后停留一段时间后立即回家。横坐标表示出行的时间,纵坐标表示小明与家的距离。
设小明家到学校的距离为$m$,小明去学校用了$a$时间,在学校停留了$b - a$时间($b$为到达学校后开始停留的时刻),回家用了$c - b$时间。
从图象可以看出,$A$点表示小明到达学校,此时横坐标为去学校所用的时间$a$,纵坐标为家到学校的距离$m$,所以$A$点坐标为$(a,m)$;$B$点表示小明回到家,此时横坐标为总时间$c$,纵坐标为$0$,所以$B$点坐标为$(c,0)$。
假设小明家到学校的距离$m = 1000$米,去学校用了$a = 10$分钟,在学校停留了$b - a = 5$分钟(即$b = 15$),回家用了$c - b = 15$分钟(即$c = 30$),则$A(10,1000)$,$B(30,0)$。
问题:小明回家的速度是多少?
根据速度公式$v = \frac{s}{t}$,$s = 1000$米,$t = 15$分钟,可得小明回家的速度$v=\frac{1000}{15}=\frac{200}{3}$(米/分钟)。
【答案】:(1)不相同。理由:设船从甲地到乙地航行和返航的路程都为$s$,从甲地到乙地航行所用时间为$t_1$,返航所用时间为$t_2$,由图象可知$t_1\lt t_2$,根据$v = \frac{s}{t}$,当$s$一定时,$t$越大,$v$越小,所以船从甲地到乙地航行的速度与返航的速度不相同,从甲地到乙地航行的速度大于返航的速度。
(2)新实际背景:小明从家出发去学校,到达学校后停留一段时间后立即回家。横坐标表示出行的时间,纵坐标表示小明与家的距离。$A(10,1000)$,$B(30,0)$(假设小明家到学校的距离$m = 1000$米,去学校用了$a = 10$分钟,在学校停留了$b - a = 5$分钟,即$b = 15$,回家用了$c - b = 15$分钟,即$c = 30$ )。问题:小明回家的速度是多少?答案:小明回家的速度是$\frac{200}{3}$米/分钟。
(1)从图象可知,船从甲地到乙地航行和返航的路程相同,设为$s$。
从甲地到乙地航行所用的时间为$t_1$,返航所用的时间为$t_2$。
根据速度公式$v = \frac{s}{t}$,从图象横坐标可以看出,从甲地到乙地航行对应的时间间隔较小,返航对应的时间间隔较大,即$t_1\lt t_2$。
因为路程$s$相同,根据$v = \frac{s}{t}$,当$s$一定时,$t$越大,$v$越小,所以船从甲地到乙地航行的速度与返航的速度不相同,从甲地到乙地航行的速度大于返航的速度。
(2)新实际背景:小明从家出发去学校,到达学校后停留一段时间后立即回家。横坐标表示出行的时间,纵坐标表示小明与家的距离。
设小明家到学校的距离为$m$,小明去学校用了$a$时间,在学校停留了$b - a$时间($b$为到达学校后开始停留的时刻),回家用了$c - b$时间。
从图象可以看出,$A$点表示小明到达学校,此时横坐标为去学校所用的时间$a$,纵坐标为家到学校的距离$m$,所以$A$点坐标为$(a,m)$;$B$点表示小明回到家,此时横坐标为总时间$c$,纵坐标为$0$,所以$B$点坐标为$(c,0)$。
假设小明家到学校的距离$m = 1000$米,去学校用了$a = 10$分钟,在学校停留了$b - a = 5$分钟(即$b = 15$),回家用了$c - b = 15$分钟(即$c = 30$),则$A(10,1000)$,$B(30,0)$。
问题:小明回家的速度是多少?
根据速度公式$v = \frac{s}{t}$,$s = 1000$米,$t = 15$分钟,可得小明回家的速度$v=\frac{1000}{15}=\frac{200}{3}$(米/分钟)。
【答案】:(1)不相同。理由:设船从甲地到乙地航行和返航的路程都为$s$,从甲地到乙地航行所用时间为$t_1$,返航所用时间为$t_2$,由图象可知$t_1\lt t_2$,根据$v = \frac{s}{t}$,当$s$一定时,$t$越大,$v$越小,所以船从甲地到乙地航行的速度与返航的速度不相同,从甲地到乙地航行的速度大于返航的速度。
(2)新实际背景:小明从家出发去学校,到达学校后停留一段时间后立即回家。横坐标表示出行的时间,纵坐标表示小明与家的距离。$A(10,1000)$,$B(30,0)$(假设小明家到学校的距离$m = 1000$米,去学校用了$a = 10$分钟,在学校停留了$b - a = 5$分钟,即$b = 15$,回家用了$c - b = 15$分钟,即$c = 30$ )。问题:小明回家的速度是多少?答案:小明回家的速度是$\frac{200}{3}$米/分钟。