你是怎样理解下列三个方程的?
(1)$2x+4= 0$;
(2)$2x+4= 1$;
(3)$2x+4= -1$.
(1)$2x+4= 0$;
(2)$2x+4= 1$;
(3)$2x+4= -1$.
答案:解:
(1)方程$2x + 4 = 0$是一元一次方程,解得$x=-2$。从一次函数角度,可看作一次函数$y=2x + 4$当$y = 0$时,求自变量$x$的值,即函数图像与$x$轴交点的横坐标为$-2$。
(2)方程$2x + 4 = 1$是一元一次方程,解得$x=-\frac{3}{2}$。从一次函数角度,可看作一次函数$y=2x + 4$当$y = 1$时,求自变量$x$的值,即函数图像上纵坐标为$1$的点的横坐标为$-\frac{3}{2}$。
(3)方程$2x + 4=-1$是一元一次方程,解得$x=-\frac{5}{2}$。从一次函数角度,可看作一次函数$y=2x + 4$当$y=-1$时,求自变量$x$的值,即函数图像上纵坐标为$-1$的点的横坐标为$-\frac{5}{2}$。
(1)方程$2x + 4 = 0$是一元一次方程,解得$x=-2$。从一次函数角度,可看作一次函数$y=2x + 4$当$y = 0$时,求自变量$x$的值,即函数图像与$x$轴交点的横坐标为$-2$。
(2)方程$2x + 4 = 1$是一元一次方程,解得$x=-\frac{3}{2}$。从一次函数角度,可看作一次函数$y=2x + 4$当$y = 1$时,求自变量$x$的值,即函数图像上纵坐标为$1$的点的横坐标为$-\frac{3}{2}$。
(3)方程$2x + 4=-1$是一元一次方程,解得$x=-\frac{5}{2}$。从一次函数角度,可看作一次函数$y=2x + 4$当$y=-1$时,求自变量$x$的值,即函数图像上纵坐标为$-1$的点的横坐标为$-\frac{5}{2}$。
例 已知一次函数$y= 2x+3的图象与正比例函数y= mx$($m$为常数,$m \neq 0$)的图象交点的横坐标是$-2$.
(1)求$m$的值;
(2)写出关于$x,y的方程组\begin{cases} 2x-y= -3, \\ mx-y= 0 \end{cases} $的解.
(1)求$m$的值;
(2)写出关于$x,y的方程组\begin{cases} 2x-y= -3, \\ mx-y= 0 \end{cases} $的解.
答案:(1)解:因为一次函数$y = 2x + 3$的图象与正比例函数$y = mx$的图象交点的横坐标是$-2$,
将$x=-2$代入$y = 2x + 3$,得$y=2×(-2)+3=-4 + 3=-1$,
所以交点坐标为$(-2,-1)$,
把$(-2,-1)$代入$y = mx$,得$-1 = m×(-2)$,
解得$m=\dfrac{1}{2}$。
(2)解:由(1)知$m = \dfrac{1}{2}$,
所以方程组为$\begin{cases}2x-y=-3\\\dfrac{1}{2}x - y=0\end{cases}$,
因为一次函数$y = 2x + 3$与$y=\dfrac{1}{2}x$的交点坐标为$(-2,-1)$,
所以方程组的解为$\begin{cases}x=-2\\y=-1\end{cases}$。
将$x=-2$代入$y = 2x + 3$,得$y=2×(-2)+3=-4 + 3=-1$,
所以交点坐标为$(-2,-1)$,
把$(-2,-1)$代入$y = mx$,得$-1 = m×(-2)$,
解得$m=\dfrac{1}{2}$。
(2)解:由(1)知$m = \dfrac{1}{2}$,
所以方程组为$\begin{cases}2x-y=-3\\\dfrac{1}{2}x - y=0\end{cases}$,
因为一次函数$y = 2x + 3$与$y=\dfrac{1}{2}x$的交点坐标为$(-2,-1)$,
所以方程组的解为$\begin{cases}x=-2\\y=-1\end{cases}$。
1. 填空题:
(1)以方程$2x-3y= 6的解(x,y)$为坐标的所有点组成的图形是函数
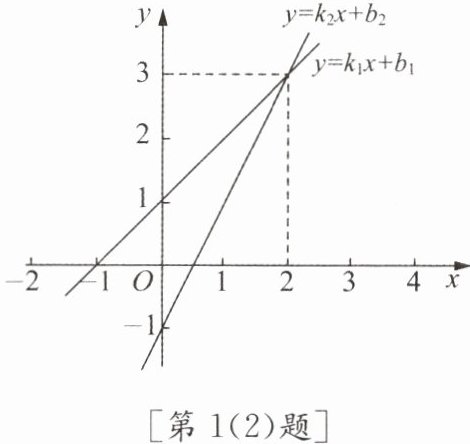
(2)如图,函数$y= k_1x+b_1与y= k_2x+b_2$的图象的交点坐标可以看作方程组
(1)以方程$2x-3y= 6的解(x,y)$为坐标的所有点组成的图形是函数
$y=\frac{2}{3}x - 2$
的图象;以方程$x+y= 4的解(x,y)$为坐标的所有点组成的图形是函数$y=-x + 4$
的图象;用函数观点看,解方程组$\begin{cases} 2x-3y= 6, \\ x+y= 4 \end{cases} $的含义是解得当自变量取$3$
时,函数$y=\frac{2}{3}x - 2$
和函数$y=-x + 4$
有相同的函数值$1$
.(2)如图,函数$y= k_1x+b_1与y= k_2x+b_2$的图象的交点坐标可以看作方程组
$\begin{cases}y = k_1x + b_1 \\ y = k_2x + b_2\end{cases}$
的解.
答案:(1) $y=\frac{2}{3}x - 2$;$y=-x + 4$;$3$;$y=\frac{2}{3}x - 2$;$y=-x + 4$;$1$
(2) $\begin{cases}y = k_1x + b_1 \\ y = k_2x + b_2\end{cases}$
(2) $\begin{cases}y = k_1x + b_1 \\ y = k_2x + b_2\end{cases}$
2. 已知一次函数$y= ax+5和y= -x+b的图象相交于点P(1,2)$.
(1)直接写出方程组$\begin{cases} ax-y= -5, \\ y+x= b \end{cases} $的解;
(2)求$a,b$的值.
(1)直接写出方程组$\begin{cases} ax-y= -5, \\ y+x= b \end{cases} $的解;
(2)求$a,b$的值.
答案:【解析】:
(1) 已知两个一次函数$y=ax+5$和$y=-x+b$在点$P(1,2)$相交,即这两个函数在点$P$的坐标满足这两个方程。因此,可以直接写出方程组的解为:
$\begin{cases}x = 1, \\y = 2.\end{cases}$
(2) 要求$a$和$b$的值,我们可以将点$P(1,2)$的坐标代入两个方程中。
对于方程$y=ax+5$,代入点$P(1,2)$得:
$2 = a \cdot 1 + 5$
解这个方程可得:
$a = 2 - 5 = -3$
对于方程$y=-x+b$,代入点$P(1,2)$得:
$2 = -1 + b$
解这个方程可得:
$b = 2 + 1 = 3$
【答案】:
(1) 方程组的解为:
$\begin{cases}x = 1, \\y = 2.\end{cases}$
(2) $a = -3, b = 3$
(1) 已知两个一次函数$y=ax+5$和$y=-x+b$在点$P(1,2)$相交,即这两个函数在点$P$的坐标满足这两个方程。因此,可以直接写出方程组的解为:
$\begin{cases}x = 1, \\y = 2.\end{cases}$
(2) 要求$a$和$b$的值,我们可以将点$P(1,2)$的坐标代入两个方程中。
对于方程$y=ax+5$,代入点$P(1,2)$得:
$2 = a \cdot 1 + 5$
解这个方程可得:
$a = 2 - 5 = -3$
对于方程$y=-x+b$,代入点$P(1,2)$得:
$2 = -1 + b$
解这个方程可得:
$b = 2 + 1 = 3$
【答案】:
(1) 方程组的解为:
$\begin{cases}x = 1, \\y = 2.\end{cases}$
(2) $a = -3, b = 3$