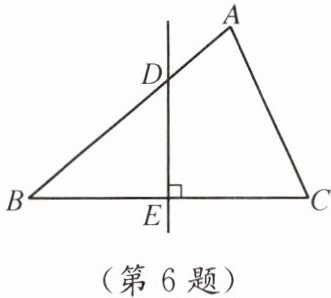
6. 如图,在△ABC中,边BC的垂直平分线DE分别与边AB,BC交于点D,E.求证:AB>AC.

答案:【解析】:
题目考查了线段垂直平分线的性质和三角形三边关系,我们需要通过连接相关线段,利用垂直平分线的性质得到相等的线段,再通过三角形三边关系来证明$AB>AC$。
连接$CD$,因为$DE$是$BC$的垂直平分线,根据垂直平分线的性质可知$BD = CD$。
在$\triangle ACD$中,根据三角形三边关系“两边之和大于第三边”,可得$AD + CD>AC$。
因为$AB = AD + BD$,且$BD = CD$,所以$AB = AD + CD$。
由$AD + CD>AC$和$AB = AD + CD$,可推出$AB>AC$。
【答案】:
证明:
连接$CD$。
∵$DE$是$BC$的垂直平分线,
∴$BD = CD$。
在$\triangle ACD$中,$AD + CD>AC$。
∵$AB = AD + BD$,$BD = CD$,
∴$AB = AD + CD$。
∴$AB>AC$。
题目考查了线段垂直平分线的性质和三角形三边关系,我们需要通过连接相关线段,利用垂直平分线的性质得到相等的线段,再通过三角形三边关系来证明$AB>AC$。
连接$CD$,因为$DE$是$BC$的垂直平分线,根据垂直平分线的性质可知$BD = CD$。
在$\triangle ACD$中,根据三角形三边关系“两边之和大于第三边”,可得$AD + CD>AC$。
因为$AB = AD + BD$,且$BD = CD$,所以$AB = AD + CD$。
由$AD + CD>AC$和$AB = AD + CD$,可推出$AB>AC$。
【答案】:
证明:
连接$CD$。
∵$DE$是$BC$的垂直平分线,
∴$BD = CD$。
在$\triangle ACD$中,$AD + CD>AC$。
∵$AB = AD + BD$,$BD = CD$,
∴$AB = AD + CD$。
∴$AB>AC$。
7. 如图,已知直线l及在其两侧的点A,B.
(1)在直线l上求作一点O,使点O到A,B两点的距离之和最短;
(2)在直线l上求作一点P,使PA= PB;
(3)在直线l上求作一点Q,使l平分∠AQB.

(1)在直线l上求作一点O,使点O到A,B两点的距离之和最短;
(2)在直线l上求作一点P,使PA= PB;
(3)在直线l上求作一点Q,使l平分∠AQB.

答案:【解析】:
(1) 本题考查了线段垂直平分线的性质以及两点之间线段最短。要使点$O$到$A$,$B$两点的距离之和最短,根据两点之间线段最短,连接$AB$,与直线$l$的交点即为所求的点$O$。
(2) 本题考查了线段垂直平分线的判定。要使$PA = PB$,根据线段垂直平分线的判定定理,到线段两个端点距离相等的点在线段的垂直平分线上,所以作线段$AB$的垂直平分线,与直线$l$的交点即为所求的点$P$。
(3) 本题考查了角平分线的判定。要使直线$l$平分$\angle AQB$,根据角平分线的判定定理,到角两边距离相等的点在角的平分线上,所以作点$A$关于直线$l$的对称点$A'$,连接$A'B$,与直线$l$的交点即为所求的点$Q$。
【答案】:
(1) 解:连接$AB$,与直线$l$相交于点$O$,则点$O$即为所求。
(2) 解:作线段$AB$的垂直平分线,与直线$l$相交于点$P$,则点$P$即为所求。
(3) 解:作点$A$关于直线$l$的对称点$A'$,连接$A'B$,与直线$l$相交于点$Q$,则点$Q$即为所求。
(1) 本题考查了线段垂直平分线的性质以及两点之间线段最短。要使点$O$到$A$,$B$两点的距离之和最短,根据两点之间线段最短,连接$AB$,与直线$l$的交点即为所求的点$O$。
(2) 本题考查了线段垂直平分线的判定。要使$PA = PB$,根据线段垂直平分线的判定定理,到线段两个端点距离相等的点在线段的垂直平分线上,所以作线段$AB$的垂直平分线,与直线$l$的交点即为所求的点$P$。
(3) 本题考查了角平分线的判定。要使直线$l$平分$\angle AQB$,根据角平分线的判定定理,到角两边距离相等的点在角的平分线上,所以作点$A$关于直线$l$的对称点$A'$,连接$A'B$,与直线$l$的交点即为所求的点$Q$。
【答案】:
(1) 解:连接$AB$,与直线$l$相交于点$O$,则点$O$即为所求。
(2) 解:作线段$AB$的垂直平分线,与直线$l$相交于点$P$,则点$P$即为所求。
(3) 解:作点$A$关于直线$l$的对称点$A'$,连接$A'B$,与直线$l$相交于点$Q$,则点$Q$即为所求。