(2)如图,AB= 4,PA= PB,QA= QB,连接P,Q交AB于点C,则AC=
2
.答案:解:∵PA=PB,
∴点P在线段AB的垂直平分线上。
∵QA=QB,
∴点Q在线段AB的垂直平分线上。
∴PQ是线段AB的垂直平分线。
∵PQ交AB于点C,
∴AC=BC。
∵AB=4,
∴AC=AB/2=4/2=2。
2
∴点P在线段AB的垂直平分线上。
∵QA=QB,
∴点Q在线段AB的垂直平分线上。
∴PQ是线段AB的垂直平分线。
∵PQ交AB于点C,
∴AC=BC。
∵AB=4,
∴AC=AB/2=4/2=2。
2
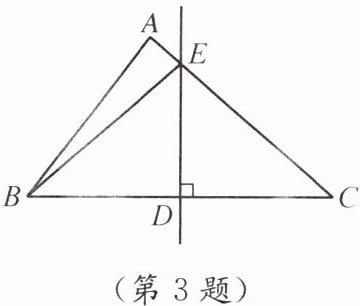
3. 如图,在△ABC中,AB<AC,边BC的垂直平分线DE与BC相交于点D,与AC相交于点E,AC= 8,△ABE的周长是14.求AB的长.

答案:解:∵DE是BC的垂直平分线,
∴EB=EC。
∵△ABE的周长是14,
∴AB+AE+EB=14。
∵EB=EC,
∴AB+AE+EC=14,即AB+AC=14。
∵AC=8,
∴AB=14-AC=14-8=6。
答:AB的长为6。
∴EB=EC。
∵△ABE的周长是14,
∴AB+AE+EB=14。
∵EB=EC,
∴AB+AE+EC=14,即AB+AC=14。
∵AC=8,
∴AB=14-AC=14-8=6。
答:AB的长为6。
4. 如图,D,E分别是AB,AC的中点,CD⊥AB,BE⊥AC,垂足分别是D,E.求证:AB= AC.


答案:【解析】:本题可根据线段垂直平分线的性质得到相等的线段,再通过全等三角形的判定和性质来证明$AB = AC$。
已知$D$是$AB$的中点且$CD\perp AB$,根据线段垂直平分线的定义可知$CD$是线段$AB$的垂直平分线。
根据线段垂直平分线的性质:线段垂直平分线上的点到这条线段的两个端点的距离相等,可得$AC = BC$(因为点$C$在$AB$的垂直平分线$CD$上)。
同理,因为$E$是$AC$的中点且$BE\perp AC$,所以$BE$是线段$AC$的垂直平分线。
根据线段垂直平分线的性质可得$AB = BC$(因为点$B$在$AC$的垂直平分线$BE$上)。
由$AC = BC$,$AB = BC$,根据等量代换可得$AB = AC$。
【答案】:
证明:
∵$D$是$AB$的中点,$CD\perp AB$,
∴$CD$是线段$AB$的垂直平分线,
∴$AC = BC$(线段垂直平分线上的点到这条线段的两个端点的距离相等)。
∵$E$是$AC$的中点,$BE\perp AC$,
∴$BE$是线段$AC$的垂直平分线,
∴$AB = BC$(线段垂直平分线上的点到这条线段的两个端点的距离相等)。
∴$AB = AC$(等量代换)。
已知$D$是$AB$的中点且$CD\perp AB$,根据线段垂直平分线的定义可知$CD$是线段$AB$的垂直平分线。
根据线段垂直平分线的性质:线段垂直平分线上的点到这条线段的两个端点的距离相等,可得$AC = BC$(因为点$C$在$AB$的垂直平分线$CD$上)。
同理,因为$E$是$AC$的中点且$BE\perp AC$,所以$BE$是线段$AC$的垂直平分线。
根据线段垂直平分线的性质可得$AB = BC$(因为点$B$在$AC$的垂直平分线$BE$上)。
由$AC = BC$,$AB = BC$,根据等量代换可得$AB = AC$。
【答案】:
证明:
∵$D$是$AB$的中点,$CD\perp AB$,
∴$CD$是线段$AB$的垂直平分线,
∴$AC = BC$(线段垂直平分线上的点到这条线段的两个端点的距离相等)。
∵$E$是$AC$的中点,$BE\perp AC$,
∴$BE$是线段$AC$的垂直平分线,
∴$AB = BC$(线段垂直平分线上的点到这条线段的两个端点的距离相等)。
∴$AB = AC$(等量代换)。
5. 如图,在△ABC中,分别画出边AB,BC的垂直平分线$l_1$和$l_2,$并相交于点O.求证:点O在边AC的垂直平分线上.


答案:【解析】:
本题考查的知识点是线段垂直平分线的性质与判定。
线段垂直平分线的性质为线段垂直平分线上的点到这条线段的两个端点的距离相等。
判定为到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上。
解题的关键是利用此性质和判定,先根据$l_1$和$l_2$分别垂直平分AB和BC,得出$OA=OB$,$OB=OC$,进而得到$OA=OC$,再根据判定得出点O在边AC的垂直平分线上。
【答案】:
证明:
∵边AB,BC的垂直平分线$l_1$和$l_2$相交于点O,
∴$OA=OB$,$OB=OC$,(线段垂直平分线上的点到这条线段的两个端点的距离相等)
∴$OA=OC$,
∴点O在边AC的垂直平分线上。(到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上)
本题考查的知识点是线段垂直平分线的性质与判定。
线段垂直平分线的性质为线段垂直平分线上的点到这条线段的两个端点的距离相等。
判定为到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上。
解题的关键是利用此性质和判定,先根据$l_1$和$l_2$分别垂直平分AB和BC,得出$OA=OB$,$OB=OC$,进而得到$OA=OC$,再根据判定得出点O在边AC的垂直平分线上。
【答案】:
证明:
∵边AB,BC的垂直平分线$l_1$和$l_2$相交于点O,
∴$OA=OB$,$OB=OC$,(线段垂直平分线上的点到这条线段的两个端点的距离相等)
∴$OA=OC$,
∴点O在边AC的垂直平分线上。(到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上)