如图1-13,要在一条笔直的路边l上修建一个燃气站,向l同侧的A,B两个城镇分别铺设管道输送燃气.要求燃气站到A,B两个城镇的距离相等,该燃气站应修建在什么位置?在图上标出它的位置.
图略(做法:分别以A,B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧交于两点,过这两点作直线,该直线与路边l的交点即为燃气站的位置)
答案:【解析】:
本题考查的知识点是线段垂直平分线的性质,即线段垂直平分线上的点到这条线段的两个端点的距离相等。
要使燃气站到$A$,$B$两个城镇的距离相等,根据线段垂直平分线的性质,可知燃气站应修建在$AB$的垂直平分线与路边$l$的交点处。
具体做法是:分别以点$A$,$B$为圆心,以大于$\frac{1}{2}AB$的长为半径画弧,两弧分别相交于两点,过这两个交点作直线,该直线就是$AB$的垂直平分线,它与路边$l$的交点就是燃气站的位置。
【答案】:
图略(做法:分别以$A$,$B$为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧交于两点,过这两点作直线,该直线与路边$l$的交点即为燃气站的位置)。
本题考查的知识点是线段垂直平分线的性质,即线段垂直平分线上的点到这条线段的两个端点的距离相等。
要使燃气站到$A$,$B$两个城镇的距离相等,根据线段垂直平分线的性质,可知燃气站应修建在$AB$的垂直平分线与路边$l$的交点处。
具体做法是:分别以点$A$,$B$为圆心,以大于$\frac{1}{2}AB$的长为半径画弧,两弧分别相交于两点,过这两个交点作直线,该直线就是$AB$的垂直平分线,它与路边$l$的交点就是燃气站的位置。
【答案】:
图略(做法:分别以$A$,$B$为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧交于两点,过这两点作直线,该直线与路边$l$的交点即为燃气站的位置)。
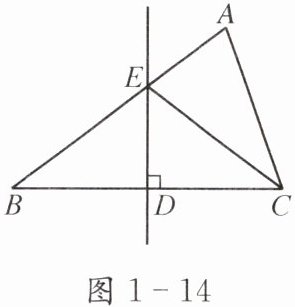
例1 如图1-14,在△ABC中,BC= 8,边BC的垂直平分线分别与边AB,BC相交于点E,D,BE= 5.求△BCE的周长.

答案:解:∵ED是BC的垂直平分线,
∴EC=BE=5(线段垂直平分线上的点到线段两端的距离相等)。
∵BC=8,
∴△BCE的周长=BE+EC+BC=5+5+8=18。
答:△BCE的周长为18。
∴EC=BE=5(线段垂直平分线上的点到线段两端的距离相等)。
∵BC=8,
∴△BCE的周长=BE+EC+BC=5+5+8=18。
答:△BCE的周长为18。
例2 如图1-15,在△ABC中,AB= AC,O是△ABC内一点,且OB= OC.求证:直线AO垂直平分线段BC.


答案:证明:
∵AB=AC,
∴点A在线段BC的垂直平分线上(到线段两端距离相等的点在这条线段的垂直平分线上)。
∵OB=OC,
∴点O在线段BC的垂直平分线上(到线段两端距离相等的点在这条线段的垂直平分线上)。
∵两点确定一条直线,
∴直线AO垂直平分线段BC。
∵AB=AC,
∴点A在线段BC的垂直平分线上(到线段两端距离相等的点在这条线段的垂直平分线上)。
∵OB=OC,
∴点O在线段BC的垂直平分线上(到线段两端距离相等的点在这条线段的垂直平分线上)。
∵两点确定一条直线,
∴直线AO垂直平分线段BC。
1.(1)线段垂直平分线上的点到
如图,∵点P在线段AB的垂直平分线l上,
∴
(2)到
如图,∵
∴点P在线段AB的垂直平分线l上.

线段两端点
的距离相等.如图,∵点P在线段AB的垂直平分线l上,
∴
PA
=PB
.(2)到
线段两端点
的距离相等的点在线段垂直平分线上.如图,∵
PA
=PB
,∴点P在线段AB的垂直平分线l上.

答案:(1)线段两端点;PA;PB
(2)线段两端点;PA;PB
(2)线段两端点;PA;PB
2.(1)如图,在△ABC中,DE,EF分别是边AB,AC的垂直平分线,AE= 3,BC= 5,则△BCE的周长是

11
.
答案:解:∵DE是AB的垂直平分线,
∴AE=BE=3。
∵EF是AC的垂直平分线,
∴AE=CE=3。
△BCE的周长=BE+CE+BC=3+3+5=11。
11
∴AE=BE=3。
∵EF是AC的垂直平分线,
∴AE=CE=3。
△BCE的周长=BE+CE+BC=3+3+5=11。
11