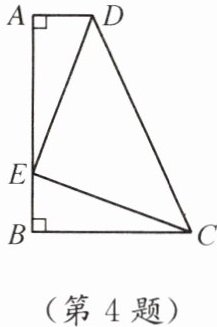
4. 如图,∠A= ∠B= 90°,点E在AB上,AE= BC,DE= CE.
(1)Rt△ADE与Rt△BEC全等吗?说明理由.
(2)△CDE是直角三角形吗?说明理由.
(1)Rt△ADE与Rt△BEC全等吗?说明理由.
(2)△CDE是直角三角形吗?说明理由.

答案:(1)Rt△ADE与Rt△BEC全等。
证明:∵∠A=∠B=90°,
∴△ADE和△BEC都是直角三角形。
在Rt△ADE和Rt△BEC中,
∵AE=BC,DE=CE,
∴Rt△ADE≌Rt△BEC(HL)。
(2)△CDE是直角三角形。
证明:∵Rt△ADE≌Rt△BEC,
∴∠ADE=∠BEC。
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=180°-90°=90°,
∴△CDE是直角三角形。
证明:∵∠A=∠B=90°,
∴△ADE和△BEC都是直角三角形。
在Rt△ADE和Rt△BEC中,
∵AE=BC,DE=CE,
∴Rt△ADE≌Rt△BEC(HL)。
(2)△CDE是直角三角形。
证明:∵Rt△ADE≌Rt△BEC,
∴∠ADE=∠BEC。
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=180°-90°=90°,
∴△CDE是直角三角形。
5. 如图,在△ABC中,BD,CE分别是边AC和AB上的高,BD= CE.求证:BE= CD.


答案:【解析】:本题可根据直角三角形全等的判定定理“HL”来证明$Rt \bigtriangleup BEC ≌ Rt \bigtriangleup CDB$,进而得出$BE = CD$。
已知$BD$,$CE$分别是边$AC$和$AB$上的高,所以$\angle BEC = \angle CDB = 90^{\circ}$。
在$Rt \bigtriangleup BEC$和$Rt \bigtriangleup CDB$中,$BD = CE$(已知),$BC$为两个直角三角形的公共边,即$BC = CB$。
根据直角三角形全等的判定定理“HL”(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt \bigtriangleup BEC ≌ Rt \bigtriangleup CDB$。
因为全等三角形的对应边相等,所以$BE = CD$。
【答案】:
证明:
∵$BD$,$CE$分别是边$AC$,$AB$上的高,
∴$\angle BEC = \angle CDB = 90^{\circ}$。
在$Rt \bigtriangleup BEC$和$Rt \bigtriangleup CDB$中,
$\begin{cases} BD = CE \\ BC = CB \end{cases}$
∴$Rt \bigtriangleup BEC ≌ Rt \bigtriangleup CDB(HL)$。
∴$BE = CD$。
已知$BD$,$CE$分别是边$AC$和$AB$上的高,所以$\angle BEC = \angle CDB = 90^{\circ}$。
在$Rt \bigtriangleup BEC$和$Rt \bigtriangleup CDB$中,$BD = CE$(已知),$BC$为两个直角三角形的公共边,即$BC = CB$。
根据直角三角形全等的判定定理“HL”(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt \bigtriangleup BEC ≌ Rt \bigtriangleup CDB$。
因为全等三角形的对应边相等,所以$BE = CD$。
【答案】:
证明:
∵$BD$,$CE$分别是边$AC$,$AB$上的高,
∴$\angle BEC = \angle CDB = 90^{\circ}$。
在$Rt \bigtriangleup BEC$和$Rt \bigtriangleup CDB$中,
$\begin{cases} BD = CE \\ BC = CB \end{cases}$
∴$Rt \bigtriangleup BEC ≌ Rt \bigtriangleup CDB(HL)$。
∴$BE = CD$。
6. 如图,在△ABC中,AD⊥BC,垂足为D,点E在边AC上,AD,BE相交于点H,且BH= AC,DH= DC.BE与AC有怎样的位置关系?证明你的结论.


答案:证明:
∵AD⊥BC,
∴∠ADB=∠ADC=90°。
在Rt△BDH和Rt△ADC中,
BH=AC,DH=DC,
∴Rt△BDH≌Rt△ADC(HL)。
∴∠HBD=∠CAD。
∵∠HBD+∠BHD=90°,∠BHD=∠AHE,
∴∠CAD+∠AHE=90°。
∴∠AEH=90°,即BE⊥AC。
结论:BE⊥AC。
∵AD⊥BC,
∴∠ADB=∠ADC=90°。
在Rt△BDH和Rt△ADC中,
BH=AC,DH=DC,
∴Rt△BDH≌Rt△ADC(HL)。
∴∠HBD=∠CAD。
∵∠HBD+∠BHD=90°,∠BHD=∠AHE,
∴∠CAD+∠AHE=90°。
∴∠AEH=90°,即BE⊥AC。
结论:BE⊥AC。
7. 如图,在Rt△ABC中,∠C= 90°,AC= 10,BC= 5,PQ= AB,P,Q两点分别在边AC和过点A且垂直于AC的射线AQ上运动.点P运动到线段AC上什么位置时,点A,P,Q组成的三角形与Rt△ABC全等?


答案:【解析】:
本题可根据全等三角形的判定定理,结合已知条件找出使得$\triangle APQ$与$Rt\triangle ABC$全等的情况,进而确定点$P$在线段$AC$上的位置。
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$PQ = AB$,$AQ\perp AC$,即$\angle QAP = 90^{\circ}=\angle C$。
全等三角形有以下几种判定情况:
当$AP = BC = 5$时:
在$Rt\triangle ABC$和$Rt\triangle QPA$中,$AB = PQ$,$BC = AP$,根据“$HL$”(斜边和一条直角边对应相等的两个直角三角形全等),因为$AB = PQ$,$BC = AP$且$\angle C=\angle QAP = 90^{\circ}$,所以$Rt\triangle ABC\cong Rt\triangle QPA$。
当$AP = AC = 10$时:
在$Rt\triangle ABC$和$Rt\triangle PAQ$中,$AB = PQ$,$AC = AP$,同样根据“$HL$”,因为$AB = PQ$,$AC = AP$且$\angle C=\angle QAP = 90^{\circ}$,所以$Rt\triangle ABC\cong Rt\triangle PAQ$。
【答案】:
当$AP = 5$或$AP = 10$时,$\triangle APQ$与$Rt\triangle ABC$全等。
即点$P$运动到$AC$中点处或点$C$处时,$\triangle APQ$与$Rt\triangle ABC$全等。
本题可根据全等三角形的判定定理,结合已知条件找出使得$\triangle APQ$与$Rt\triangle ABC$全等的情况,进而确定点$P$在线段$AC$上的位置。
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$PQ = AB$,$AQ\perp AC$,即$\angle QAP = 90^{\circ}=\angle C$。
全等三角形有以下几种判定情况:
当$AP = BC = 5$时:
在$Rt\triangle ABC$和$Rt\triangle QPA$中,$AB = PQ$,$BC = AP$,根据“$HL$”(斜边和一条直角边对应相等的两个直角三角形全等),因为$AB = PQ$,$BC = AP$且$\angle C=\angle QAP = 90^{\circ}$,所以$Rt\triangle ABC\cong Rt\triangle QPA$。
当$AP = AC = 10$时:
在$Rt\triangle ABC$和$Rt\triangle PAQ$中,$AB = PQ$,$AC = AP$,同样根据“$HL$”,因为$AB = PQ$,$AC = AP$且$\angle C=\angle QAP = 90^{\circ}$,所以$Rt\triangle ABC\cong Rt\triangle PAQ$。
【答案】:
当$AP = 5$或$AP = 10$时,$\triangle APQ$与$Rt\triangle ABC$全等。
即点$P$运动到$AC$中点处或点$C$处时,$\triangle APQ$与$Rt\triangle ABC$全等。