画Rt△ABC,使∠C= 90°,AB= 3 cm,AC= 2 cm.你画的直角三角形与其他同学画的直角三角形全等吗?为什么?
答案:解:画图步骤:
1. 画∠MCN=90°;
2. 在射线CM上截取CA=2cm;
3. 以A为圆心,3cm为半径画弧,交射线CN于点B;
4. 连接AB,Rt△ABC即为所求。
全等。
证明:在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C'=2cm,AB=A'B'=3cm,根据斜边直角边定理(HL),Rt△ABC≌Rt△A'B'C'。
1. 画∠MCN=90°;
2. 在射线CM上截取CA=2cm;
3. 以A为圆心,3cm为半径画弧,交射线CN于点B;
4. 连接AB,Rt△ABC即为所求。
全等。
证明:在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C'=2cm,AB=A'B'=3cm,根据斜边直角边定理(HL),Rt△ABC≌Rt△A'B'C'。
例 如图1-12,E是AB延长线上一点,AC⊥BC,AD⊥BD,垂足分别为C,D,AC= AD.求证:∠CEA= ∠DEA.
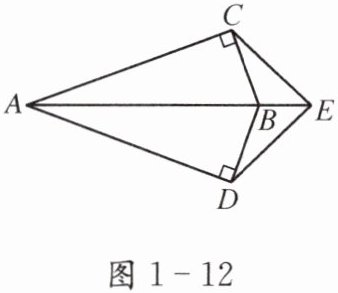

答案:证明:
∵AC⊥BC,AD⊥BD,
∴∠ACB=∠ADB=90°,
在Rt△ACB和Rt△ADB中,
AC=AD,AB=AB,
∴Rt△ACB≌Rt△ADB(HL),
∴BC=BD,
在△BCE和△BDE中,
BC=BD,∠CBE=∠DBE,BE=BE,
∴△BCE≌△BDE(SAS),
∴∠CEA=∠DEA.
∵AC⊥BC,AD⊥BD,
∴∠ACB=∠ADB=90°,
在Rt△ACB和Rt△ADB中,
AC=AD,AB=AB,
∴Rt△ACB≌Rt△ADB(HL),
∴BC=BD,
在△BCE和△BDE中,
BC=BD,∠CBE=∠DBE,BE=BE,
∴△BCE≌△BDE(SAS),
∴∠CEA=∠DEA.
1. 斜边和
如图,在Rt△ABC和Rt△A'B'C'中,∠A= ∠A'= 90°,
∵AB=
∴Rt△ABC≌Rt△A'B'C'(
一条直角边
分别相等的两个直角三角形全等(简写成斜边、直角边(或 HL)
).如图,在Rt△ABC和Rt△A'B'C'中,∠A= ∠A'= 90°,
∵AB=
A'B'
,BC=B'C'
,∴Rt△ABC≌Rt△A'B'C'(
HL
).答案:【解析】:
本题考查直角三角形全等的一个判定定理,即斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”。
在题目所给的$Rt\bigtriangleup ABC$和$Rt\bigtriangleup A'B'C'$中,已知$\angle A = \angle A' = 90^{\circ}$,要使$Rt\bigtriangleup ABC\cong Rt\bigtriangleup A'B'C'$,根据“HL”定理,需要斜边相等且一条直角边相等,从图中可知斜边为$BC$和$B'C'$,一条直角边为$AB$和$A'B'$,所以应填$A'B'$,$B'C'$,判定定理为“HL”。
【答案】:
一条直角边;斜边、直角边(或 HL);$A'B'$;$B'C'$;HL
本题考查直角三角形全等的一个判定定理,即斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”。
在题目所给的$Rt\bigtriangleup ABC$和$Rt\bigtriangleup A'B'C'$中,已知$\angle A = \angle A' = 90^{\circ}$,要使$Rt\bigtriangleup ABC\cong Rt\bigtriangleup A'B'C'$,根据“HL”定理,需要斜边相等且一条直角边相等,从图中可知斜边为$BC$和$B'C'$,一条直角边为$AB$和$A'B'$,所以应填$A'B'$,$B'C'$,判定定理为“HL”。
【答案】:
一条直角边;斜边、直角边(或 HL);$A'B'$;$B'C'$;HL
2. 在下列四组条件中,能判定Rt△ABC≌Rt△A'B'C'(其中∠C= ∠C'= 90°)的是
①②④
(填序号).答案:解:①在Rt△ABC和Rt△A'B'C'中,
∵∠C=∠C'=90°,∠A=∠A',AC=A'C',
∴Rt△ABC≌Rt△A'B'C'(ASA)。
②在Rt△ABC和Rt△A'B'C'中,
∵AC=A'C',∠C=∠C'=90°,BC=B'C',
∴Rt△ABC≌Rt△A'B'C'(SAS)。
③仅有∠A=∠A',∠B=∠B',没有边对应相等,不能判定全等。
④在Rt△ABC和Rt△A'B'C'中,
∵AC=A'C',AB=A'B',∠C=∠C'=90°,
∴Rt△ABC≌Rt△A'B'C'(HL)。
能判定全等的是①②④。
答案:①②④
∵∠C=∠C'=90°,∠A=∠A',AC=A'C',
∴Rt△ABC≌Rt△A'B'C'(ASA)。
②在Rt△ABC和Rt△A'B'C'中,
∵AC=A'C',∠C=∠C'=90°,BC=B'C',
∴Rt△ABC≌Rt△A'B'C'(SAS)。
③仅有∠A=∠A',∠B=∠B',没有边对应相等,不能判定全等。
④在Rt△ABC和Rt△A'B'C'中,
∵AC=A'C',AB=A'B',∠C=∠C'=90°,
∴Rt△ABC≌Rt△A'B'C'(HL)。
能判定全等的是①②④。
答案:①②④
3. 判断题(正确的打“√”,错误的打“×”):
(1)一个锐角及斜边分别相等的两个直角三角形全等;(
(2)两条边分别相等的两个直角三角形全等;(
(3)一条直角边和斜边分别相等的两个直角三角形全等.(
(1)一个锐角及斜边分别相等的两个直角三角形全等;(
√
)(2)两条边分别相等的两个直角三角形全等;(
×
)(3)一条直角边和斜边分别相等的两个直角三角形全等.(
√
)答案:【解析】:
本题主要考察直角三角形全等的判定条件。
(1) 对于第一个判断题,根据直角三角形的性质,如果一个锐角和斜边分别相等,那么这两个直角三角形可以通过$AAS$(Angle-Angle-Side)判定为全等。具体到直角三角形,由于已知一个锐角和直角,再加上斜边,就构成了$AAS$条件,因此可以判定两个直角三角形全等。所以第一个判断题是正确的。
(2) 对于第二个判断题,两条边分别相等的条件并不足以判定两个直角三角形全等。因为这里的两条边可能是两条直角边,也可能是直角边和斜边,或者是两条斜边(实际上在直角三角形中两条斜边不可能相等,这里只是为了说明情况)。在没有其他信息的情况下,不能确保两个三角形全等。所以第二个判断题是错误的。
(3) 对于第三个判断题,根据直角三角形的$HL$(Hypotenuse-Leg)判定定理,如果一条直角边和斜边分别相等,那么这两个直角三角形可以判定为全等。所以第三个判断题是正确的。
【答案】:
(1) √
(2) ×
(3) √
本题主要考察直角三角形全等的判定条件。
(1) 对于第一个判断题,根据直角三角形的性质,如果一个锐角和斜边分别相等,那么这两个直角三角形可以通过$AAS$(Angle-Angle-Side)判定为全等。具体到直角三角形,由于已知一个锐角和直角,再加上斜边,就构成了$AAS$条件,因此可以判定两个直角三角形全等。所以第一个判断题是正确的。
(2) 对于第二个判断题,两条边分别相等的条件并不足以判定两个直角三角形全等。因为这里的两条边可能是两条直角边,也可能是直角边和斜边,或者是两条斜边(实际上在直角三角形中两条斜边不可能相等,这里只是为了说明情况)。在没有其他信息的情况下,不能确保两个三角形全等。所以第二个判断题是错误的。
(3) 对于第三个判断题,根据直角三角形的$HL$(Hypotenuse-Leg)判定定理,如果一条直角边和斜边分别相等,那么这两个直角三角形可以判定为全等。所以第三个判断题是正确的。
【答案】:
(1) √
(2) ×
(3) √