1.(1)角平分线上的点到
如图,∵点P在∠AOB的平分线上,
∴
(2)角的内部到
如图,∵
∴点P在∠AOB的平分线上.
]
]
角两边
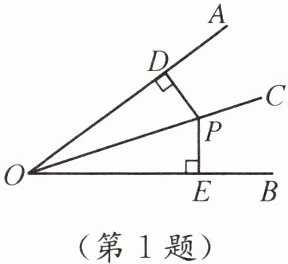
相等.如图,∵点P在∠AOB的平分线上,
PD
⊥OA
,PE
⊥OB
,∴
PD
=PE
.(2)角的内部到
角两边距离
相等的点在角的平分线上.如图,∵
PD
⊥OA
,PE
⊥OB
,PD
=PE
,∴点P在∠AOB的平分线上.
]
]

答案:【解析】:
本题主要考查角平分线的性质定理及其逆定理。
(1) 角平分线上的点到角两边的距离相等。
根据题目条件,点P在$\angle AOB$的平分线上,$PD$垂直于$OA$,$PE$垂直于$OB$。
所以,可以根据角平分线的性质得出$PD = PE$。
(2) 角的内部到角两边距离相等的点在角的平分线上。
根据题目条件,$PD$垂直于$OA$,$PE$垂直于$OB$,且$PD = PE$。
所以,可以根据角平分线的逆定理得出点P在$\angle AOB$的平分线上。
【答案】:
(1) 角两边;$PD$;$OA$;$PE$;$OB$;$PD$;$PE$
(2) 角两边距离;$PD$;$OA$;$PE$;$OB$;$PD$;$PE$
本题主要考查角平分线的性质定理及其逆定理。
(1) 角平分线上的点到角两边的距离相等。
根据题目条件,点P在$\angle AOB$的平分线上,$PD$垂直于$OA$,$PE$垂直于$OB$。
所以,可以根据角平分线的性质得出$PD = PE$。
(2) 角的内部到角两边距离相等的点在角的平分线上。
根据题目条件,$PD$垂直于$OA$,$PE$垂直于$OB$,且$PD = PE$。
所以,可以根据角平分线的逆定理得出点P在$\angle AOB$的平分线上。
【答案】:
(1) 角两边;$PD$;$OA$;$PE$;$OB$;$PD$;$PE$
(2) 角两边距离;$PD$;$OA$;$PE$;$OB$;$PD$;$PE$
2.(1)如图,∠C= 90°,∠1= ∠2,已知BC= 10,BD= 6,则点D到AB的距离为______.


(2)如图,在△ABC中,AB= 5,AC= 4,BC= 6,AP平分∠BAC,交BC于点P,则S△ABP∶S△ACP= ______,BP的长为______.


(2)如图,在△ABC中,AB= 5,AC= 4,BC= 6,AP平分∠BAC,交BC于点P,则S△ABP∶S△ACP= ______,BP的长为______.
答案:(1)解:过点D作DE⊥AB于E,
∵∠C=90°,∠1=∠2,
∴DC=DE(角平分线上的点到角两边距离相等),
∵BC=10,BD=6,
∴DC=BC-BD=10-6=4,
∴DE=4,即点D到AB的距离为4。
(2)解:过点P作PD⊥AB于D,PE⊥AC于E,
∵AP平分∠BAC,
∴PD=PE(角平分线上的点到角两边距离相等),
∵S△ABP=$\frac{1}{2}$AB·PD,S△ACP=$\frac{1}{2}$AC·PE,
∴S△ABP∶S△ACP=AB∶AC=5∶4;
设BP=x,则PC=6-x,
∵S△ABP∶S△ACP=BP∶PC(等高三角形面积比等于底之比),
∴5∶4=x∶(6-x),
解得x=$\frac{10}{3}$,即BP的长为$\frac{10}{3}$。
答案:(1)4;(2)5∶4;$\frac{10}{3}$
∵∠C=90°,∠1=∠2,
∴DC=DE(角平分线上的点到角两边距离相等),
∵BC=10,BD=6,
∴DC=BC-BD=10-6=4,
∴DE=4,即点D到AB的距离为4。
(2)解:过点P作PD⊥AB于D,PE⊥AC于E,
∵AP平分∠BAC,
∴PD=PE(角平分线上的点到角两边距离相等),
∵S△ABP=$\frac{1}{2}$AB·PD,S△ACP=$\frac{1}{2}$AC·PE,
∴S△ABP∶S△ACP=AB∶AC=5∶4;
设BP=x,则PC=6-x,
∵S△ABP∶S△ACP=BP∶PC(等高三角形面积比等于底之比),
∴5∶4=x∶(6-x),
解得x=$\frac{10}{3}$,即BP的长为$\frac{10}{3}$。
答案:(1)4;(2)5∶4;$\frac{10}{3}$
3. 如图,用直尺和圆规在直线l上找到一点P,使点P到∠O的两边OA,OB的距离相等.


答案:解:1. 以点O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
2. 分别以点C、D为圆心,大于$\frac{1}{2}CD$长为半径画弧,两弧在∠AOB内部交于点E;
3. 作射线OE;
4. 射线OE与直线l的交点即为所求点P。
2. 分别以点C、D为圆心,大于$\frac{1}{2}CD$长为半径画弧,两弧在∠AOB内部交于点E;
3. 作射线OE;
4. 射线OE与直线l的交点即为所求点P。
4. 如图,在△ABC中,AD是角平分线,点P在AD上,PE//AB,交BC于点E,PF//AC,交BC于点F.求证:点D到PE和PF的距离相等.


答案:【解析】:
本题主要考查角平分线的性质,即角平分线上的点到角两边的距离相等,以及平行线的性质。
证明过程中,先根据平行线的性质得到一些角相等关系,再结合角平分线的定义推出相关角相等,进而得到$PE$和$PF$与角两边夹角的关系,最后利用角平分线的性质证明点$D$到$PE$和$PF$的距离相等。
【答案】:
证明:
∵$PE// AB$,$PF// AC$,
∴$\angle EPD = \angle BAD$,$\angle FPD = \angle CAD$(两直线平行,内错角相等)。
∵$AD$是角平分线,
∴$\angle BAD = \angle CAD$(角平分线的定义)。
∴$\angle EPD = \angle FPD$(等量代换)。
∵$PD$是角$\angle EPF$的平分线(角平分线的定义)。
根据角平分线的性质:角平分线上的点到角两边的距离相等。
所以点$D$到$PE$和$PF$的距离相等。
本题主要考查角平分线的性质,即角平分线上的点到角两边的距离相等,以及平行线的性质。
证明过程中,先根据平行线的性质得到一些角相等关系,再结合角平分线的定义推出相关角相等,进而得到$PE$和$PF$与角两边夹角的关系,最后利用角平分线的性质证明点$D$到$PE$和$PF$的距离相等。
【答案】:
证明:
∵$PE// AB$,$PF// AC$,
∴$\angle EPD = \angle BAD$,$\angle FPD = \angle CAD$(两直线平行,内错角相等)。
∵$AD$是角平分线,
∴$\angle BAD = \angle CAD$(角平分线的定义)。
∴$\angle EPD = \angle FPD$(等量代换)。
∵$PD$是角$\angle EPF$的平分线(角平分线的定义)。
根据角平分线的性质:角平分线上的点到角两边的距离相等。
所以点$D$到$PE$和$PF$的距离相等。