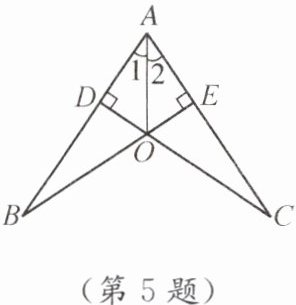
5. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB= OC.求证:∠1= ∠2.

答案:证明:
∵CD⊥AB,BE⊥AC,
∴∠ODB=∠OEC=90°。
在△ODB和△OEC中,
∠ODB=∠OEC,
∠DOB=∠EOC(对顶角相等),
OB=OC,
∴△ODB≌△OEC(AAS)。
∴OD=OE。
∵OD⊥AB,OE⊥AC,
∴AO平分∠BAC,即∠1=∠2。
∵CD⊥AB,BE⊥AC,
∴∠ODB=∠OEC=90°。
在△ODB和△OEC中,
∠ODB=∠OEC,
∠DOB=∠EOC(对顶角相等),
OB=OC,
∴△ODB≌△OEC(AAS)。
∴OD=OE。
∵OD⊥AB,OE⊥AC,
∴AO平分∠BAC,即∠1=∠2。
6. 如图,∠B= ∠C= 90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.


答案:【解析】:
本题可根据角平分线的性质定理,通过作辅助线构造全等三角形,进而证明$AE$是$\angle DAB$的平分线。
证明思路为:过点$E$作$EF\perp AD$于点$F$,先根据角平分线的性质得到$EC = EF$,再结合$E$是$BC$中点得到$EB = EF$,最后根据角平分线的判定定理证明$AE$是$\angle DAB$的平分线。
【答案】:
证明:
过点$E$作$EF\perp AD$于点$F$。
∵$DE$平分$\angle ADC$,$\angle C = 90^{\circ}$(即$EC\perp DC$),$EF\perp AD$,
根据角平分线的性质:角平分线上的点到角两边的距离相等,
∴$EC = EF$。
∵$E$是$BC$的中点,
∴$EB = EC$。
又∵$EC = EF$,
∴$EB = EF$。
∵$\angle B = 90^{\circ}$(即$EB\perp AB$),$EF\perp AD$,
根据角平分线的判定定理:到角两边距离相等的点在这个角的平分线上,
∴点$E$在$\angle DAB$的平分线上,即$AE$是$\angle DAB$的平分线。
本题可根据角平分线的性质定理,通过作辅助线构造全等三角形,进而证明$AE$是$\angle DAB$的平分线。
证明思路为:过点$E$作$EF\perp AD$于点$F$,先根据角平分线的性质得到$EC = EF$,再结合$E$是$BC$中点得到$EB = EF$,最后根据角平分线的判定定理证明$AE$是$\angle DAB$的平分线。
【答案】:
证明:
过点$E$作$EF\perp AD$于点$F$。
∵$DE$平分$\angle ADC$,$\angle C = 90^{\circ}$(即$EC\perp DC$),$EF\perp AD$,
根据角平分线的性质:角平分线上的点到角两边的距离相等,
∴$EC = EF$。
∵$E$是$BC$的中点,
∴$EB = EC$。
又∵$EC = EF$,
∴$EB = EF$。
∵$\angle B = 90^{\circ}$(即$EB\perp AB$),$EF\perp AD$,
根据角平分线的判定定理:到角两边距离相等的点在这个角的平分线上,
∴点$E$在$\angle DAB$的平分线上,即$AE$是$\angle DAB$的平分线。
7. 如图,OC是∠AOB的角平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E. F是OC上的另一点,连接DF,EF.求证:DF= EF.


答案:【解析】:
本题主要考查角平分线的性质以及全等三角形的判定与性质,可通过证明三角形全等得出$DF = EF$。
步骤一:根据角平分线的性质得到线段相等
已知$OC$是$\angle AOB$的角平分线,$PD\perp OA$,$PE\perp OB$,根据角平分线的性质:角平分线上的点到角两边的距离相等,可得$PD = PE$。
步骤二:证明$\angle PDF = \angle PEF$
因为$PD\perp OA$,$PE\perp OB$,所以$\angle PDO = \angle PEO = 90^{\circ}$。
又因为$\angle AOC = \angle BOC$($OC$是角平分线),$OP = OP$(公共边),根据全等三角形判定定理$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ODP\cong\triangle OEP$,则$\angle DPO = \angle EPO$。
因为$\angle DPF = 180^{\circ} - \angle DPO$,$\angle EPF = 180^{\circ} - \angle EPO$,所以$\angle DPF = \angle EPF$。
在$\triangle PDF$和$\triangle PEF$中,$PD = PE$,$\angle DPF = \angle EPF$,$PF = PF$(公共边),根据全等三角形判定定理$SAS$(两边及其夹角对应相等的两个三角形全等),可得$\triangle PDF\cong\triangle PEF$。
步骤三:根据全等三角形的性质得出结论
由于$\triangle PDF\cong\triangle PEF$,根据全等三角形的性质:全等三角形的对应边相等,所以$DF = EF$。
【答案】:
证明:
∵$OC$是$\angle AOB$的角平分线,$PD\perp OA$,$PE\perp OB$,
∴$PD = PE$。
∵$\angle PDO = \angle PEO = 90^{\circ}$,$\angle AOC = \angle BOC$,$OP = OP$,
∴$\triangle ODP\cong\triangle OEP(AAS)$,
∴$\angle DPO = \angle EPO$。
∵$\angle DPF = 180^{\circ} - \angle DPO$,$\angle EPF = 180^{\circ} - \angle EPO$,
∴$\angle DPF = \angle EPF$。
在$\triangle PDF$和$\triangle PEF$中,
$\begin{cases}PD = PE\\\angle DPF = \angle EPF\\PF = PF\end{cases}$
∴$\triangle PDF\cong\triangle PEF(SAS)$,
∴$DF = EF$。
本题主要考查角平分线的性质以及全等三角形的判定与性质,可通过证明三角形全等得出$DF = EF$。
步骤一:根据角平分线的性质得到线段相等
已知$OC$是$\angle AOB$的角平分线,$PD\perp OA$,$PE\perp OB$,根据角平分线的性质:角平分线上的点到角两边的距离相等,可得$PD = PE$。
步骤二:证明$\angle PDF = \angle PEF$
因为$PD\perp OA$,$PE\perp OB$,所以$\angle PDO = \angle PEO = 90^{\circ}$。
又因为$\angle AOC = \angle BOC$($OC$是角平分线),$OP = OP$(公共边),根据全等三角形判定定理$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ODP\cong\triangle OEP$,则$\angle DPO = \angle EPO$。
因为$\angle DPF = 180^{\circ} - \angle DPO$,$\angle EPF = 180^{\circ} - \angle EPO$,所以$\angle DPF = \angle EPF$。
在$\triangle PDF$和$\triangle PEF$中,$PD = PE$,$\angle DPF = \angle EPF$,$PF = PF$(公共边),根据全等三角形判定定理$SAS$(两边及其夹角对应相等的两个三角形全等),可得$\triangle PDF\cong\triangle PEF$。
步骤三:根据全等三角形的性质得出结论
由于$\triangle PDF\cong\triangle PEF$,根据全等三角形的性质:全等三角形的对应边相等,所以$DF = EF$。
【答案】:
证明:
∵$OC$是$\angle AOB$的角平分线,$PD\perp OA$,$PE\perp OB$,
∴$PD = PE$。
∵$\angle PDO = \angle PEO = 90^{\circ}$,$\angle AOC = \angle BOC$,$OP = OP$,
∴$\triangle ODP\cong\triangle OEP(AAS)$,
∴$\angle DPO = \angle EPO$。
∵$\angle DPF = 180^{\circ} - \angle DPO$,$\angle EPF = 180^{\circ} - \angle EPO$,
∴$\angle DPF = \angle EPF$。
在$\triangle PDF$和$\triangle PEF$中,
$\begin{cases}PD = PE\\\angle DPF = \angle EPF\\PF = PF\end{cases}$
∴$\triangle PDF\cong\triangle PEF(SAS)$,
∴$DF = EF$。