我们已经知道线段和角都是轴对称图形,多边形是否也具有轴对称性?举例说明.
答案:多边形不一定都具有轴对称性。
例如:正方形是轴对称图形,它有4条对称轴;一般的平行四边形不是轴对称图形。
例如:正方形是轴对称图形,它有4条对称轴;一般的平行四边形不是轴对称图形。
例1 等腰三角形的周长为20,其中一条边长为6,求另外两条边的长.
答案:【解析】:
本题主要考察等腰三角形的性质以及三角形的周长计算。
由于题目没有指明已知的边长是否为腰长,所以需要分两种情况讨论。
第一种情况,假设已知的边长$6$是等腰三角形的腰长,那么根据等腰三角形的性质,另一条腰长也为$6$。
由三角形的周长公式,可以求出底边的长度:
$20 - 6 - 6 = 8$。
再根据三角形的三边关系(任意两边之和大于第三边),可以验证$6, 6, 8$能否构成三角形:
$6 + 6 > 8$,$6 + 8 > 6$,$6 + 8 > 6$,满足条件。
第二种情况,假设已知的边长$6$是等腰三角形的底边,那么根据等腰三角形的性质,两条腰长相等。
设腰长为$x$,则三角形的周长为:
$6 + 2x = 20$。
解这个方程,得到:
$2x = 14$,$x = 7$。
再根据三角形的三边关系,可以验证$7, 7, 6$能否构成三角形:
$7 + 7 > 6$,$7 + 6 > 7$,$7 + 6 > 7$,满足条件。
【答案】:
另外两条边的长分别为$6, 8$或$7, 7$。
本题主要考察等腰三角形的性质以及三角形的周长计算。
由于题目没有指明已知的边长是否为腰长,所以需要分两种情况讨论。
第一种情况,假设已知的边长$6$是等腰三角形的腰长,那么根据等腰三角形的性质,另一条腰长也为$6$。
由三角形的周长公式,可以求出底边的长度:
$20 - 6 - 6 = 8$。
再根据三角形的三边关系(任意两边之和大于第三边),可以验证$6, 6, 8$能否构成三角形:
$6 + 6 > 8$,$6 + 8 > 6$,$6 + 8 > 6$,满足条件。
第二种情况,假设已知的边长$6$是等腰三角形的底边,那么根据等腰三角形的性质,两条腰长相等。
设腰长为$x$,则三角形的周长为:
$6 + 2x = 20$。
解这个方程,得到:
$2x = 14$,$x = 7$。
再根据三角形的三边关系,可以验证$7, 7, 6$能否构成三角形:
$7 + 7 > 6$,$7 + 6 > 7$,$7 + 6 > 7$,满足条件。
【答案】:
另外两条边的长分别为$6, 8$或$7, 7$。
例2 如图1-19,在△ABC中,AB= AC,点D在边AC上,BD= BC= AD.求△ABC的各角度数.
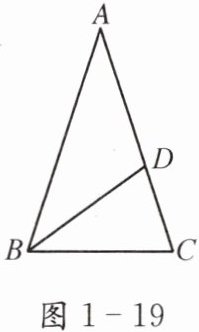

答案:【解析】:本题可根据等腰三角形的性质,结合三角形内角和定理以及三角形外角的性质来求解$\triangle ABC$各角的度数。
步骤一:设未知数表示角的度数
设$\angle A = x$,因为$AD = BD$,根据等腰三角形两底角相等的性质,可知$\angle ABD=\angle A = x$。
步骤二:求出$\angle BDC$的度数
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABD$中,$\angle BDC$是$\triangle ABD$的一个外角,所以$\angle BDC=\angle A + \angle ABD = 2x$。
步骤三:求出$\angle C$和$\angle ABC$的度数
因为$BD = BC$,所以$\angle C=\angle BDC = 2x$。
又因为$AB = AC$,所以$\angle ABC=\angle C = 2x$。
步骤四:根据三角形内角和定理列方程求解
在$\triangle ABC$中,根据三角形内角和定理:三角形内角和为$180^{\circ}$,可得$\angle A + \angle ABC + \angle C = 180^{\circ}$,即$x + 2x + 2x = 180^{\circ}$。
合并同类项可得$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
步骤五:求出$\triangle ABC$各角的度数
将$x = 36^{\circ}$代入$\angle A = x$,$\angle ABC = 2x$,$\angle C = 2x$,可得$\angle A = 36^{\circ}$,$\angle ABC = 72^{\circ}$,$\angle C = 72^{\circ}$。
【答案】:$\angle A = 36^{\circ}$,$\angle ABC = 72^{\circ}$,$\angle C = 72^{\circ}$。
步骤一:设未知数表示角的度数
设$\angle A = x$,因为$AD = BD$,根据等腰三角形两底角相等的性质,可知$\angle ABD=\angle A = x$。
步骤二:求出$\angle BDC$的度数
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABD$中,$\angle BDC$是$\triangle ABD$的一个外角,所以$\angle BDC=\angle A + \angle ABD = 2x$。
步骤三:求出$\angle C$和$\angle ABC$的度数
因为$BD = BC$,所以$\angle C=\angle BDC = 2x$。
又因为$AB = AC$,所以$\angle ABC=\angle C = 2x$。
步骤四:根据三角形内角和定理列方程求解
在$\triangle ABC$中,根据三角形内角和定理:三角形内角和为$180^{\circ}$,可得$\angle A + \angle ABC + \angle C = 180^{\circ}$,即$x + 2x + 2x = 180^{\circ}$。
合并同类项可得$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
步骤五:求出$\triangle ABC$各角的度数
将$x = 36^{\circ}$代入$\angle A = x$,$\angle ABC = 2x$,$\angle C = 2x$,可得$\angle A = 36^{\circ}$,$\angle ABC = 72^{\circ}$,$\angle C = 72^{\circ}$。
【答案】:$\angle A = 36^{\circ}$,$\angle ABC = 72^{\circ}$,$\angle C = 72^{\circ}$。
1.(1)等腰三角形的
如图,∵AB= AC,
∴
(2)等腰三角形
如图,∵AB= AC,AD⊥BC,
∴
∵AB= AC,BD= CD,
∴
∵AB= AC,∠BAD= ∠CAD,
∴

两底角
相等.如图,∵AB= AC,
∴
∠B
=∠C
.(2)等腰三角形
顶角的平分线
、底边上的中线
及底边上的高
重合.如图,∵AB= AC,AD⊥BC,
∴
BD=CD
,∠BAD=∠CAD
.∵AB= AC,BD= CD,
∴
AD⊥BC
,∠BAD=∠CAD
.∵AB= AC,∠BAD= ∠CAD,
∴
AD⊥BC
,BD=CD
.
答案:(1) 两底角;∠B;∠C
(2) 顶角的平分线;底边上的中线;底边上的高;BD=CD;∠BAD=∠CAD;AD⊥BC;∠BAD=∠CAD;AD⊥BC;BD=CD
(2) 顶角的平分线;底边上的中线;底边上的高;BD=CD;∠BAD=∠CAD;AD⊥BC;∠BAD=∠CAD;AD⊥BC;BD=CD
2. 选择题:
(1)下列长度的3条线段,能组成等腰三角形的是(
A. 2 cm,2 cm,4 cm
B. 3 cm,4 cm,6 cm
C. 3 cm,3 cm,8 cm
D. 4 cm,4 cm,5 cm
(2)在下列图形中,不一定是轴对称图形的是(
A. 角
B. 等腰三角形
C. 直角三角形
D. 等腰直角三角形
(3)已知一个等腰三角形的两条边长分别为2,4,则这个等腰三角形的周长是(
A. 6
B. 8
C. 10
D. 8或10
(1)下列长度的3条线段,能组成等腰三角形的是(
D
).A. 2 cm,2 cm,4 cm
B. 3 cm,4 cm,6 cm
C. 3 cm,3 cm,8 cm
D. 4 cm,4 cm,5 cm
(2)在下列图形中,不一定是轴对称图形的是(
C
).A. 角
B. 等腰三角形
C. 直角三角形
D. 等腰直角三角形
(3)已知一个等腰三角形的两条边长分别为2,4,则这个等腰三角形的周长是(
C
).A. 6
B. 8
C. 10
D. 8或10
答案:【解析】:
本题主要考察等腰三角形的性质以及三角形的三边关系。
(1) 对于选项A,有两条边长度为2 cm,但第三条边为4 cm,由于$2+2=4$,不满足三角形的三边关系(任意两边之和大于第三边),所以不能组成三角形,故A错误。
对于选项B,三条边长度分别为3 cm, 4 cm, 6 cm,满足三角形的三边关系,但没有两边相等,所以不是等腰三角形,故B错误。
对于选项C,有两条边长度为3 cm,但第三条边为8 cm,由于$3+3<8$,不满足三角形的三边关系,所以不能组成三角形,故C错误。
对于选项D,有两条边长度为4 cm,第三条边为5 cm,满足三角形的三边关系,且是等腰三角形,故D正确。
(2) 对于选项A,角一定是轴对称图形,对称轴是角的平分线所在的直线,故A错误。
对于选项B,等腰三角形一定是轴对称图形,对称轴是底边的垂直平分线,故B错误。
对于选项C,直角三角形不一定是轴对称图形,只有当它是等腰直角三角形时才是轴对称图形,故C正确。
对于选项D,等腰直角三角形一定是轴对称图形,对称轴是底边的垂直平分线,也是直角顶角的平分线,故D错误。
(3) 对于等腰三角形的两条边长分别为2和4,需要分两种情况考虑:
当腰长为2时,三边长为2, 2, 4。由于$2+2=4$,不满足三角形的三边关系,所以这种情况不成立。
当腰长为4时,三边长为4, 4, 2。满足三角形的三边关系,且周长为$4+4+2=10$。
【答案】:
(1) D
(2) C
(3) C
本题主要考察等腰三角形的性质以及三角形的三边关系。
(1) 对于选项A,有两条边长度为2 cm,但第三条边为4 cm,由于$2+2=4$,不满足三角形的三边关系(任意两边之和大于第三边),所以不能组成三角形,故A错误。
对于选项B,三条边长度分别为3 cm, 4 cm, 6 cm,满足三角形的三边关系,但没有两边相等,所以不是等腰三角形,故B错误。
对于选项C,有两条边长度为3 cm,但第三条边为8 cm,由于$3+3<8$,不满足三角形的三边关系,所以不能组成三角形,故C错误。
对于选项D,有两条边长度为4 cm,第三条边为5 cm,满足三角形的三边关系,且是等腰三角形,故D正确。
(2) 对于选项A,角一定是轴对称图形,对称轴是角的平分线所在的直线,故A错误。
对于选项B,等腰三角形一定是轴对称图形,对称轴是底边的垂直平分线,故B错误。
对于选项C,直角三角形不一定是轴对称图形,只有当它是等腰直角三角形时才是轴对称图形,故C正确。
对于选项D,等腰直角三角形一定是轴对称图形,对称轴是底边的垂直平分线,也是直角顶角的平分线,故D错误。
(3) 对于等腰三角形的两条边长分别为2和4,需要分两种情况考虑:
当腰长为2时,三边长为2, 2, 4。由于$2+2=4$,不满足三角形的三边关系,所以这种情况不成立。
当腰长为4时,三边长为4, 4, 2。满足三角形的三边关系,且周长为$4+4+2=10$。
【答案】:
(1) D
(2) C
(3) C