3. 填空题:
(1)在△ABC中,AB= AC,∠B= 80°,∠C=
(2)等腰三角形的一个外角等于140°,这个等腰三角形的顶角的度数是
(1)在△ABC中,AB= AC,∠B= 80°,∠C=
80
°,∠A= 20
°;(2)等腰三角形的一个外角等于140°,这个等腰三角形的顶角的度数是
40°或100°
.答案:
(1)80;20
(2)40°或100°
(1)80;20
(2)40°或100°
4.(1)如图,在△ABC中,AB= AC,AD⊥BC,垂足为D.求证:BD= CD,∠BAD= ∠CAD.
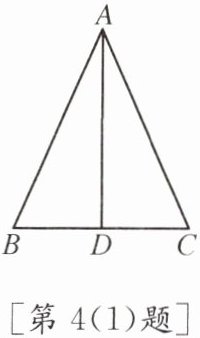
(2)如图,在△ABC中,AB= AC,∠BAD= ∠CAD.求证:AD⊥BC,BD= CD.

(3)如图,在△ABC中,AB= AC,BD= CD.求证:AD⊥BC,∠BAD= ∠CAD.


(2)如图,在△ABC中,AB= AC,∠BAD= ∠CAD.求证:AD⊥BC,BD= CD.

(3)如图,在△ABC中,AB= AC,BD= CD.求证:AD⊥BC,∠BAD= ∠CAD.

答案:4.(1)证明:∵AB=AC,AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
$\left\{\begin{array}{l} AB=AC\\ AD=AD\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,∠BAD=∠CAD;
(2)证明:在△ABD和△ACD中,
$\left\{\begin{array}{l} AB=AC\\ ∠BAD=∠CAD\\ AD=AD\end{array}\right.$,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC;
(3)证明:在△ABD和△ACD中,
$\left\{\begin{array}{l} AB=AC\\ AD=AD\\ BD=CD\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC.
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
$\left\{\begin{array}{l} AB=AC\\ AD=AD\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,∠BAD=∠CAD;
(2)证明:在△ABD和△ACD中,
$\left\{\begin{array}{l} AB=AC\\ ∠BAD=∠CAD\\ AD=AD\end{array}\right.$,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC;
(3)证明:在△ABD和△ACD中,
$\left\{\begin{array}{l} AB=AC\\ AD=AD\\ BD=CD\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC.