剪一张锐角三角形纸片,你能用折纸的方法分别折出这个三角形的一条角平分线、中线和高吗?折折看.
答案:解:能。
角平分线:将三角形的一个角的两边重合对折,折痕即为该角的角平分线。
中线:将三角形的一个顶点与对边中点重合对折(使对边两端点重合,折痕与对边交点为中点),连接顶点与中点的折痕即为该边上的中线。
高:将三角形的一条边对折,使这条边与它自身重合,得到这条边的垂线,过相对顶点的折痕即为该边上的高。
角平分线:将三角形的一个角的两边重合对折,折痕即为该角的角平分线。
中线:将三角形的一个顶点与对边中点重合对折(使对边两端点重合,折痕与对边交点为中点),连接顶点与中点的折痕即为该边上的中线。
高:将三角形的一条边对折,使这条边与它自身重合,得到这条边的垂线,过相对顶点的折痕即为该边上的高。
(1)在△ADC中,边AD上的高是
(2)在△AEC中,边CE上的高是
(3)在△FEA中,边EA上的高是
(4)已知AB= CD= 4,CE= 6,则△AEC的面积S=
CD
;(2)在△AEC中,边CE上的高是
AB
;(3)在△FEA中,边EA上的高是
FE
;(4)已知AB= CD= 4,CE= 6,则△AEC的面积S=
12
,AE=6
.答案:
(1) CD
(2) AB
(3) FE
(4) 12;6
(1) CD
(2) AB
(3) FE
(4) 12;6
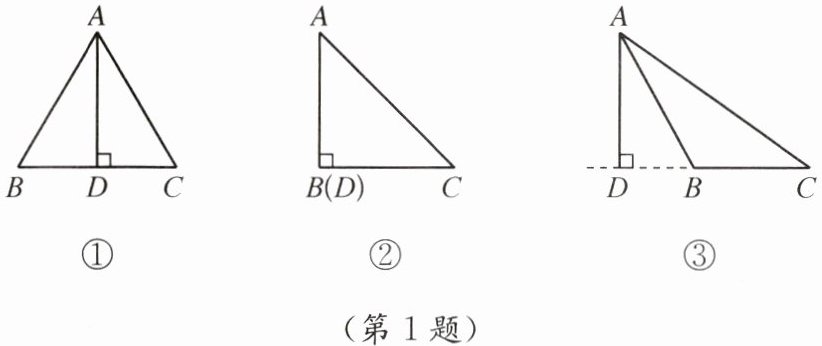
1. 如图,在△ABC中,AD是边BC上的高,图①、图②和图③中的三个∠ABC有什么不同?AD在各自三角形的什么位置?你能说出其中的规律吗?

答案:【解析】:
本题主要考查三角形的高这一概念。
在三角形中,从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
对于图①,$\angle ABC$是锐角,此时高$AD$在三角形$ABC$的内部。
对于图②,$\angle ABC$是直角,此时高$AD$与直角边$AB$重合,也就是在三角形的直角边上。
对于图③,$\angleABC$是钝角,此时高$AD$在三角形$ABC$的外部。
规律为:锐角三角形三条高都在三角形内部;直角三角形有两条高即两条直角边,一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部。
【答案】:
图①中$\angle ABC$是锐角,$AD$在$\bigtriangleup ABC$内部;
图②中$\angle ABC$是直角,$AD$在$\bigtriangleup ABC$的直角边上;
图③中$\angle ABC$是钝角,$AD$在$\bigtriangleup ABC$外部。
规律:锐角三角形三条高都在三角形内部;直角三角形有两条高即两条直角边,一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部。
本题主要考查三角形的高这一概念。
在三角形中,从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
对于图①,$\angle ABC$是锐角,此时高$AD$在三角形$ABC$的内部。
对于图②,$\angle ABC$是直角,此时高$AD$与直角边$AB$重合,也就是在三角形的直角边上。
对于图③,$\angleABC$是钝角,此时高$AD$在三角形$ABC$的外部。
规律为:锐角三角形三条高都在三角形内部;直角三角形有两条高即两条直角边,一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部。
【答案】:
图①中$\angle ABC$是锐角,$AD$在$\bigtriangleup ABC$内部;
图②中$\angle ABC$是直角,$AD$在$\bigtriangleup ABC$的直角边上;
图③中$\angle ABC$是钝角,$AD$在$\bigtriangleup ABC$外部。
规律:锐角三角形三条高都在三角形内部;直角三角形有两条高即两条直角边,一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部。
2. (1)如图①,线段AD,BE,CF是△ABC的三条中线,则AB= 2

(2)如图②,线段AD,BE,CF是△ABC的三条角平分线,则∠1=
BF
,BD= DC
,AE= $\frac{1}{2}$AC
;
(2)如图②,线段AD,BE,CF是△ABC的三条角平分线,则∠1=
∠2
,∠3= $\frac{1}{2}$∠ABC
,∠ACB= 2∠4
.答案:(1)BF;DC;AC
(2)∠2;∠ABC;∠4
(2)∠2;∠ABC;∠4