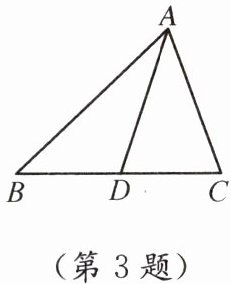
3.(1)如图,在△ABC中,点D在边BC上,连接AD.图中有
(2)在△ABC中,已知AC<AB<BC,那么∠A,∠B,∠C的大小关系是
3
个三角形,它们分别是:△ABC,△ABD,△ACD
.
(2)在△ABC中,已知AC<AB<BC,那么∠A,∠B,∠C的大小关系是
∠B<∠C<∠A
.(用“<”号连接)答案:【解析】:
(1) 对于第一个问题,需要数出图中三角形的个数,并列举出它们。
从图中可以看到,除了原三角形$ABC$外,还有由点$A$, $D$与原三角形的边构成的三角形$ABD$和$ACD$。
(2) 对于第二个问题,根据三角形的性质,大边对大角进行分析,即在三角形中,较长的一边对应的角也较大。
题目给出了边的长度关系 $AC < AB < BC$,可以直接得出角的大小关系为 $∠B < ∠C < ∠A$。
【答案】:
(1) $3$;$△ABC$,$△ABD$,$△ACD$
(2) $∠B < ∠C< ∠A$
(1) 对于第一个问题,需要数出图中三角形的个数,并列举出它们。
从图中可以看到,除了原三角形$ABC$外,还有由点$A$, $D$与原三角形的边构成的三角形$ABD$和$ACD$。
(2) 对于第二个问题,根据三角形的性质,大边对大角进行分析,即在三角形中,较长的一边对应的角也较大。
题目给出了边的长度关系 $AC < AB < BC$,可以直接得出角的大小关系为 $∠B < ∠C < ∠A$。
【答案】:
(1) $3$;$△ABC$,$△ABD$,$△ACD$
(2) $∠B < ∠C< ∠A$
4. 用11根火柴棒首尾相连搭成一个三角形,能搭出多少种不同的三角形?写出每种三角形三边的火柴棒根数.
答案:解:设三角形三边的火柴棒根数分别为$a$,$b$,$c$,且$a \leq b \leq c$,则$a + b + c = 11$,$a + b > c$。
因为$a \leq b \leq c$,所以$c \geq \frac{11}{3} \approx 3.67$,又$a + b > c$,即$11 - c > c$,所以$c < 5.5$,故$c$可取4,5。
当$c = 5$时,$a + b = 6$,则$b \geq a$,$b \leq 5$,$a \leq b$,可得:
$a = 2$,$b = 4$,$c = 5$
$a = 3$,$b = 3$,$c = 5$
当$c = 4$时,$a + b = 7$,则$b \leq 4$,$a \leq b$,可得:
$a = 3$,$b = 4$,$c = 4$
综上,能搭出3种不同的三角形,三边火柴棒根数分别为:
1. 2, 4, 5
2. 3, 3, 5
3. 3, 4, 4
因为$a \leq b \leq c$,所以$c \geq \frac{11}{3} \approx 3.67$,又$a + b > c$,即$11 - c > c$,所以$c < 5.5$,故$c$可取4,5。
当$c = 5$时,$a + b = 6$,则$b \geq a$,$b \leq 5$,$a \leq b$,可得:
$a = 2$,$b = 4$,$c = 5$
$a = 3$,$b = 3$,$c = 5$
当$c = 4$时,$a + b = 7$,则$b \leq 4$,$a \leq b$,可得:
$a = 3$,$b = 4$,$c = 4$
综上,能搭出3种不同的三角形,三边火柴棒根数分别为:
1. 2, 4, 5
2. 3, 3, 5
3. 3, 4, 4
5. 用一根长为18 cm的细绳围成一个等腰三角形.
(1)已知腰长是底边长的2倍,各边的长分别是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?若能,各边的长是多少?
(1)已知腰长是底边长的2倍,各边的长分别是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?若能,各边的长是多少?
答案:【解析】:
本题主要考查等腰三角形的性质以及三角形的三边关系。
(1) 设底边长为 $x$ cm,则腰长为 $2x$ cm。
由等腰三角形的性质知,两腰相等,所以两腰的总长为 $2 × 2x = 4x$ cm。
三角形的周长为底边加两腰,即 $x + 4x = 18$。
解得 $x = \frac{18}{5} = 3.6$ cm。
所以,腰长为 $2 × 3.6 = 7.2$ cm。
因此,等腰三角形的三边长分别为 7.2 cm,7.2 cm,3.6 cm。
(2) 分两种情况考虑:
当4 cm为底边时:
腰长为 $\frac{18 - 4}{2} = 7$ cm。
由三角形的三边关系知,任意两边之和大于第三边,所以 $4 + 7 > 7$ 且 $7 + 7 > 4$,满足条件。
因此,当4 cm为底边时,三边长为 4 cm,7 cm,7 cm。
当4 cm为腰长时:
底边长为 $18 - 4 × 2 = 10$ cm。
但由三角形的三边关系知,$4 + 4 < 10$,不满足条件,所以这种情况应舍去。
综上,能围成有一边长为4 cm的等腰三角形,且各边的长为 4 cm,7 cm,7 cm。
【答案】:
(1) 三边长分别为 7.2 cm,7.2 cm,3.6 cm。
(2) 能围成有一边长为4 cm的等腰三角形,各边的长为 4 cm,7 cm,7 cm。
本题主要考查等腰三角形的性质以及三角形的三边关系。
(1) 设底边长为 $x$ cm,则腰长为 $2x$ cm。
由等腰三角形的性质知,两腰相等,所以两腰的总长为 $2 × 2x = 4x$ cm。
三角形的周长为底边加两腰,即 $x + 4x = 18$。
解得 $x = \frac{18}{5} = 3.6$ cm。
所以,腰长为 $2 × 3.6 = 7.2$ cm。
因此,等腰三角形的三边长分别为 7.2 cm,7.2 cm,3.6 cm。
(2) 分两种情况考虑:
当4 cm为底边时:
腰长为 $\frac{18 - 4}{2} = 7$ cm。
由三角形的三边关系知,任意两边之和大于第三边,所以 $4 + 7 > 7$ 且 $7 + 7 > 4$,满足条件。
因此,当4 cm为底边时,三边长为 4 cm,7 cm,7 cm。
当4 cm为腰长时:
底边长为 $18 - 4 × 2 = 10$ cm。
但由三角形的三边关系知,$4 + 4 < 10$,不满足条件,所以这种情况应舍去。
综上,能围成有一边长为4 cm的等腰三角形,且各边的长为 4 cm,7 cm,7 cm。
【答案】:
(1) 三边长分别为 7.2 cm,7.2 cm,3.6 cm。
(2) 能围成有一边长为4 cm的等腰三角形,各边的长为 4 cm,7 cm,7 cm。
6. 已知:如图,在△ABC中,点P在△ABC内部.
求证:AC+CB>AP+PB.

求证:AC+CB>AP+PB.

答案:证明:
延长$BP$交$AC$于点$D$。
在$\triangle ABD$中,根据三角形三边关系“两边之和大于第三边”,可得$AD + PD>AP$ ①;
在$\triangle DCB$中,同理可得$DC + CB>DP + PB$ ②;
将①$+$②可得:
$AD+ PD + DC + CB>AP + DP + PB$,
两边同时减去$PD $,AD+DC=AC,得到:
$AC + CB>AP + PB$。
延长$BP$交$AC$于点$D$。
在$\triangle ABD$中,根据三角形三边关系“两边之和大于第三边”,可得$AD + PD>AP$ ①;
在$\triangle DCB$中,同理可得$DC + CB>DP + PB$ ②;
将①$+$②可得:
$AD+ PD + DC + CB>AP + DP + PB$,
两边同时减去$PD $,AD+DC=AC,得到:
$AC + CB>AP + PB$。