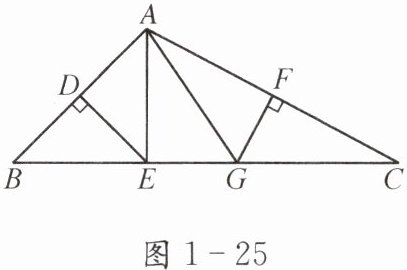
例1 如图1-25,在△ABC中,边AB的垂直平分线分别与边AB,BC交于点D,E,边AC的垂直平分线分别与边AC,BC交于点F,G.求△AEG的周长需要添加什么条件? 求∠EAG的度数需要添加什么条件?

答案:解:
1. 求△AEG的周长需要添加的条件:BC的长。
理由:∵DE垂直平分AB,∴EA=EB;∵FG垂直平分AC,∴GA=GC。
∴△AEG的周长=EA+EG+GA=EB+EG+GC=BC。
2. 求∠EAG的度数需要添加的条件:∠B和∠C的度数(或∠BAC的度数)。
理由:设∠B=x,∠C=y,则∠BAC=180°-x-y。
∵EA=EB,GA=GC,∴∠EAB=∠B=x,∠GAC=∠C=y。
∴∠EAG=∠BAC-∠EAB-∠GAC=180°-x-y-x-y=180°-2(x+y)(或直接用∠BAC -∠B -∠C)。
结论:求△AEG的周长需添加BC的长;求∠EAG的度数需添加∠B和∠C的度数(或∠BAC的度数)。
1. 求△AEG的周长需要添加的条件:BC的长。
理由:∵DE垂直平分AB,∴EA=EB;∵FG垂直平分AC,∴GA=GC。
∴△AEG的周长=EA+EG+GA=EB+EG+GC=BC。
2. 求∠EAG的度数需要添加的条件:∠B和∠C的度数(或∠BAC的度数)。
理由:设∠B=x,∠C=y,则∠BAC=180°-x-y。
∵EA=EB,GA=GC,∴∠EAB=∠B=x,∠GAC=∠C=y。
∴∠EAG=∠BAC-∠EAB-∠GAC=180°-x-y-x-y=180°-2(x+y)(或直接用∠BAC -∠B -∠C)。
结论:求△AEG的周长需添加BC的长;求∠EAG的度数需添加∠B和∠C的度数(或∠BAC的度数)。
例2 如图1-26,在△ABC中,分别以AB,AC为边作等边三角形ABE和等边三角形ACD,BD,CE相交于点O.
(1) BD与CE相等吗?为什么?
(2) 要使△ABE与△ACD全等,至少需要添加什么条件?在此条件下,整个图形是轴对称图形吗?

(1) BD与CE相等吗?为什么?
(2) 要使△ABE与△ACD全等,至少需要添加什么条件?在此条件下,整个图形是轴对称图形吗?

答案:【解析】:
(1)本题可根据等边三角形的性质得出相关边和角的关系,再通过全等三角形的判定定理证明$\triangle ABD\cong\triangle EAC$,进而得出$BD$与$CE$的关系。
步骤一:分析等边三角形的性质
已知$\triangle ABE$和$\triangle ACD$都是等边三角形,根据等边三角形的性质可知:
$AB = AE$,$AD = AC$;
$\angle BAE = \angle CAD = 60^{\circ}$。
步骤二:求出$\angle BAD$与$\angle EAC$的关系
因为$\angle BAE + \angle BAC = \angle CAD + \angle BAC$,所以$\angle BAD = \angle EAC$。
步骤三:证明$\triangle ABD\cong\triangle EAC$
在$\triangle ABD$和$\triangle EAC$中,$\begin{cases}AB = AE\\\angle BAD = \angle EAC\\AD = AC\end{cases}$,根据全等三角形的判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle ABD\cong\triangle EAC$。
步骤四:得出$BD$与$CE$的关系
由于全等三角形的对应边相等,因为$\triangle ABD\cong\triangle EAC$,所以$BD = CE$。
(2)本题可根据全等三角形的判定条件来确定使$\triangle ABE$与$\triangle ACD$全等需要添加的条件,再根据轴对称图形的定义判断整个图形是否为轴对称图形。
步骤一:确定使$\triangle ABE$与$\triangle ACD$全等需要添加的条件
已知$\triangle ABE$和$\triangle ACD$都是等边三角形,则$AB = AE$,$AC = AD$,$\angle BAE = \angle CAD = 60^{\circ}$。
根据全等三角形的判定定理($SAS$:两边及其夹角对应相等的三角形全等),当$AB = AC$(或$AE = AD$)时,$\triangle ABE\cong\triangle ACD$。
步骤二:判断整个图形是否为轴对称图形
当$AB = AC$时,因为$\triangle ABE$和$\triangle ACD$是等边三角形,所以$AB = AE = AC = AD$,$\angle BAE = \angle CAD = 60^{\circ}$,则$\angle BAC = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ}$。
此时$\triangle ABC$和$\triangle ADE$都是等边三角形,整个图形关于直线$AO$对称($AO$是$\angle BAC$和$\angle DAE$的角平分线),所以整个图形是轴对称图形。
【答案】:
(1)$BD$与$CE$相等。理由如下:
$\because\triangle ABE$和$\triangle ACD$都是等边三角形,
$\therefore AB = AE$,$AD = AC$,$\angle BAE = \angle CAD = 60^{\circ}$。
$\because\angle BAE + \angle BAC = \angle CAD + \angle BAC$,
$\therefore\angle BAD = \angle EAC$。
在$\triangle ABD$和$\triangle EAC$中,$\begin{cases}AB = AE\\\angle BAD = \angle EAC\\AD = AC\end{cases}$,
$\therefore\triangle ABD\cong\triangle EAC(SAS)$,
$\therefore BD = CE$。
(2)添加条件$AB = AC$(或$AE = AD$)。在此条件下,整个图形是轴对称图形。
(1)本题可根据等边三角形的性质得出相关边和角的关系,再通过全等三角形的判定定理证明$\triangle ABD\cong\triangle EAC$,进而得出$BD$与$CE$的关系。
步骤一:分析等边三角形的性质
已知$\triangle ABE$和$\triangle ACD$都是等边三角形,根据等边三角形的性质可知:
$AB = AE$,$AD = AC$;
$\angle BAE = \angle CAD = 60^{\circ}$。
步骤二:求出$\angle BAD$与$\angle EAC$的关系
因为$\angle BAE + \angle BAC = \angle CAD + \angle BAC$,所以$\angle BAD = \angle EAC$。
步骤三:证明$\triangle ABD\cong\triangle EAC$
在$\triangle ABD$和$\triangle EAC$中,$\begin{cases}AB = AE\\\angle BAD = \angle EAC\\AD = AC\end{cases}$,根据全等三角形的判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle ABD\cong\triangle EAC$。
步骤四:得出$BD$与$CE$的关系
由于全等三角形的对应边相等,因为$\triangle ABD\cong\triangle EAC$,所以$BD = CE$。
(2)本题可根据全等三角形的判定条件来确定使$\triangle ABE$与$\triangle ACD$全等需要添加的条件,再根据轴对称图形的定义判断整个图形是否为轴对称图形。
步骤一:确定使$\triangle ABE$与$\triangle ACD$全等需要添加的条件
已知$\triangle ABE$和$\triangle ACD$都是等边三角形,则$AB = AE$,$AC = AD$,$\angle BAE = \angle CAD = 60^{\circ}$。
根据全等三角形的判定定理($SAS$:两边及其夹角对应相等的三角形全等),当$AB = AC$(或$AE = AD$)时,$\triangle ABE\cong\triangle ACD$。
步骤二:判断整个图形是否为轴对称图形
当$AB = AC$时,因为$\triangle ABE$和$\triangle ACD$是等边三角形,所以$AB = AE = AC = AD$,$\angle BAE = \angle CAD = 60^{\circ}$,则$\angle BAC = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ}$。
此时$\triangle ABC$和$\triangle ADE$都是等边三角形,整个图形关于直线$AO$对称($AO$是$\angle BAC$和$\angle DAE$的角平分线),所以整个图形是轴对称图形。
【答案】:
(1)$BD$与$CE$相等。理由如下:
$\because\triangle ABE$和$\triangle ACD$都是等边三角形,
$\therefore AB = AE$,$AD = AC$,$\angle BAE = \angle CAD = 60^{\circ}$。
$\because\angle BAE + \angle BAC = \angle CAD + \angle BAC$,
$\therefore\angle BAD = \angle EAC$。
在$\triangle ABD$和$\triangle EAC$中,$\begin{cases}AB = AE\\\angle BAD = \angle EAC\\AD = AC\end{cases}$,
$\therefore\triangle ABD\cong\triangle EAC(SAS)$,
$\therefore BD = CE$。
(2)添加条件$AB = AC$(或$AE = AD$)。在此条件下,整个图形是轴对称图形。