例3 阅读并回答问题:
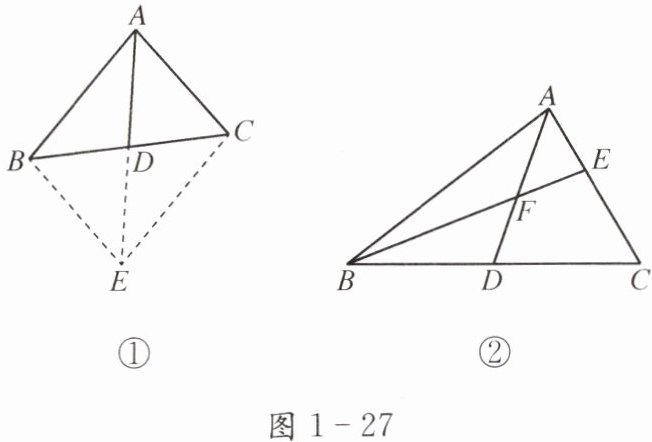
如图1-27①,在△ABC中,AD为中线,延长AD到点E,使DE= AD.在△ABD和△ECD中,AD= ED,∠ADB= ∠EDC,BD= CD,所以△ABD≌△ECD(SAS),进一步可得AB= EC,AB//CE等结论.
已知三角形的中线时,我们常用"倍长中线"的方法构造全等三角形,解决相关的计算或证明.
解决问题:如图1-27②,在△ABC中,AD是△ABC的中线,点F在中线AD上,连接并延长BF交AC于点E,且BF= AC.求证:∠AFE= ∠CAF.
如图1-27①,在△ABC中,AD为中线,延长AD到点E,使DE= AD.在△ABD和△ECD中,AD= ED,∠ADB= ∠EDC,BD= CD,所以△ABD≌△ECD(SAS),进一步可得AB= EC,AB//CE等结论.
已知三角形的中线时,我们常用"倍长中线"的方法构造全等三角形,解决相关的计算或证明.
解决问题:如图1-27②,在△ABC中,AD是△ABC的中线,点F在中线AD上,连接并延长BF交AC于点E,且BF= AC.求证:∠AFE= ∠CAF.

答案:【解析】:本题考查全等三角形的判定与性质。
根据题意,我们需要通过“倍长中线”的方法构造全等三角形。
第一步,延长$AD$至点$G$,使$DG = AD$,并连接$BG$。
由于$AD$是$\bigtriangleup ABC$的中线,根据中线的性质,我们有$BD = CD$。
在$\bigtriangleup ADC$和$\bigtriangleup GDB$中,由于$AD = GD$,$\angle ADC = \angle GDB$(对顶角),且$CD = BD$,根据$SAS$全等条件,我们得到$\bigtriangleup ADC ≌ \bigtriangleup GDB$。
由于$\bigtriangleup ADC ≌ \bigtriangleup GDB$,根据全等三角形的性质,我们有$BG = AC$,且$\angle CAD = \angle G$。
又因为题目给出$BF = AC$,所以$BG = BF$。
由于$BG = BF$,根据等腰三角形的性质,我们得到$\angle G = \angle BFG$。
又因为对顶角相等,即$\angle BFG = \angle AFE$,所以$\angle G = \angle AFE$。
由于之前已经得到$\angle CAD = \angle G$,所以$\angle AFE = \angle CAF$。
【答案】:证明:
延长$AD$至点$G$,使$DG = AD$,连接$BG$。
在$\bigtriangleup ADC$和$\bigtriangleup GDB$中,
$\left\{\begin{array}{l} AD = GD, \\ \angle ADC = \angle GDB, \\ CD = BD. \end{array} \right.$
∴ $\bigtriangleup ADC ≌ \bigtriangleup GDB (SAS)$。
∴ $BG = AC$,$\angle CAD = \angle G$。
∵ $BF = AC$,
∴ $BG = BF$。
∴ $\angle G = \angle BFG$。
∵ $\angle BFG = \angle AFE$,
∴ $\angle G = \angle AFE$。
∴ $\angle AFE = \angle CAF$。
根据题意,我们需要通过“倍长中线”的方法构造全等三角形。
第一步,延长$AD$至点$G$,使$DG = AD$,并连接$BG$。
由于$AD$是$\bigtriangleup ABC$的中线,根据中线的性质,我们有$BD = CD$。
在$\bigtriangleup ADC$和$\bigtriangleup GDB$中,由于$AD = GD$,$\angle ADC = \angle GDB$(对顶角),且$CD = BD$,根据$SAS$全等条件,我们得到$\bigtriangleup ADC ≌ \bigtriangleup GDB$。
由于$\bigtriangleup ADC ≌ \bigtriangleup GDB$,根据全等三角形的性质,我们有$BG = AC$,且$\angle CAD = \angle G$。
又因为题目给出$BF = AC$,所以$BG = BF$。
由于$BG = BF$,根据等腰三角形的性质,我们得到$\angle G = \angle BFG$。
又因为对顶角相等,即$\angle BFG = \angle AFE$,所以$\angle G = \angle AFE$。
由于之前已经得到$\angle CAD = \angle G$,所以$\angle AFE = \angle CAF$。
【答案】:证明:
延长$AD$至点$G$,使$DG = AD$,连接$BG$。
在$\bigtriangleup ADC$和$\bigtriangleup GDB$中,
$\left\{\begin{array}{l} AD = GD, \\ \angle ADC = \angle GDB, \\ CD = BD. \end{array} \right.$
∴ $\bigtriangleup ADC ≌ \bigtriangleup GDB (SAS)$。
∴ $BG = AC$,$\angle CAD = \angle G$。
∵ $BF = AC$,
∴ $BG = BF$。
∴ $\angle G = \angle BFG$。
∵ $\angle BFG = \angle AFE$,
∴ $\angle G = \angle AFE$。
∴ $\angle AFE = \angle CAF$。
1. 选择题:
(1) 已知三角形的两边长分别是2,4,则第三边的边长可以是(
A. 1
B. 2
C. 5
D. 6
(2) 下列说法中,正确的是(
A. 周长相等的两个锐角三角形全等
B. 周长相等的两个直角三角形全等
C. 周长相等的两个等腰三角形全等
D. 周长相等的两个等边三角形全等
(3) 如图,BE⊥AC,CF⊥AB,垂足分别为E,F,BE= CF,则图中全等三角形有(
A. 1对


B. 2对
C. 3对
D. 4对
(4) 如图,在三角形纸片ABC中,AC= BC,把△ABC沿着AC向下翻折,使点B落在点D处,连接BD.已知∠BAC= 40°,那么∠CBD的度数为(
A. 9°
B. 10°
C. 20°
D. 30°
(1) 已知三角形的两边长分别是2,4,则第三边的边长可以是(
C
).A. 1
B. 2
C. 5
D. 6
(2) 下列说法中,正确的是(
D
).A. 周长相等的两个锐角三角形全等
B. 周长相等的两个直角三角形全等
C. 周长相等的两个等腰三角形全等
D. 周长相等的两个等边三角形全等
(3) 如图,BE⊥AC,CF⊥AB,垂足分别为E,F,BE= CF,则图中全等三角形有(
B
).A. 1对


B. 2对
C. 3对
D. 4对
(4) 如图,在三角形纸片ABC中,AC= BC,把△ABC沿着AC向下翻折,使点B落在点D处,连接BD.已知∠BAC= 40°,那么∠CBD的度数为(
B
).A. 9°
B. 10°
C. 20°
D. 30°
答案:【解析】:
(1) 本题考察的是三角形三边关系“两边之和大于第三边,两边之差小于第三边”。
已知两边长分别是2和4,设第三边长为$x$,根据三角形三边关系可得:
$4 - 2 \lt x \lt 4 + 2$,即$2 \lt x \lt 6$。
逐一分析选项:
选项A:$1\lt 2$,不满足$2 \lt x \lt 6$,所以A选项错误。
选项B:$2 = 2$,不满足$2 \lt x \lt 6$,所以B选项错误。
选项C:$2\lt 5\lt 6$,满足$2 \lt x \lt 6$,所以C选项正确。
选项D:$6 = 6$,不满足$2 \lt x \lt 6$,所以D选项错误。
(2) 本题可根据全等三角形的判定定理,逐一分析每个选项。
选项A:周长相等的两个锐角三角形,只能说明它们三边之和相等,但三边的长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个锐角三角形不一定全等,A选项错误。
选项B:周长相等的两个直角三角形,同样只能说明三边之和相等,三边长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个直角三角形不一定全等,B选项错误。
选项C:周长相等的两个等腰三角形,只能确定两腰与底边之和相等,但两腰和底边的长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个等腰三角形不一定全等,C选项错误。
选项D:因为等边三角形的三边都相等,周长相等的两个等边三角形,其三边长度必然对应相等。
根据全等三角形判定定理“边边边”(SSS),三边对应相等的两个三角形全等,所以周长相等的两个等边三角形全等,D选项正确。
(3) 本题可根据全等三角形的判定定理,结合已知条件$BE\perp AC$,$CF\perp AB$,$BE = CF$,找出图中的全等三角形。
已知$BE\perp AC$,$CF\perp AB$,则$\angle AEB=\angle AFC = 90^{\circ}$。
在$\triangle ABE$和$\triangle ACF$中:
$\begin{cases} \angle AEB=\angle AFC,\\ \angle BAE=\angle CAF,\\ BE = CF. \end{cases}$
根据全等三角形判定定理“角角边”(AAS),可得$\triangle ABE\cong\triangle ACF$。
因为$AB = AC$(由$\triangle ABE\cong\triangle ACF$可得),$BE\perp AC$,$CF\perp AB$,$BE = CF$,在$\triangle BCE$和$\triangle CBF$中:
$\begin{cases} \angle BEC=\angle CFB = 90^{\circ},\\ BC = CB,\\ BE = CF. \end{cases}$
根据全等三角形判定定理“斜边直角边”(HL),可得$\triangle BCE\cong\triangle CBF$。
所以图中全等三角形有$\triangle ABE\cong\triangle ACF$,$\triangle BCE\cong\triangle CBF$,共$2$对,B选项正确。
(4) 本题可先根据等腰三角形的性质求出$\angle ACB$的度数,再根据折叠的性质得到相关角的关系,进而求出$\angle CBD$的度数。
因为$AC = BC$,$\angle BAC = 40^{\circ}$,根据等腰三角形两底角相等以及三角形内角和为$180^{\circ}$,可得:
$\angle ABC=\angle ACB=\frac{1}{2}×(180^{\circ}-\angle BAC)=\frac{1}{2}×(180^{\circ} - 40^{\circ}) = 70^{\circ}$。
由折叠的性质可知:$\triangle ABC\cong\triangle ADC$,所以$\angle D=\angle ABC = 70^{\circ}$,$BC = DC$。
因为$BC = DC$,所以$\angle CBD=\angle D = 70^{\circ}$。
在$\triangle BCD$中,$\angle CBD=\angle D = 70^{\circ}$,根据三角形内角和为$180^{\circ}$,可得:
$\angle BCD=180^{\circ}-2×70^{\circ}= 40^{\circ}$。
则$\angle ABD=\angle ABC-\angle CBD=70^{\circ}- \angle CBD$。
又因为$\angle ABC = 70^{\circ}$,$\angle BCD = 40^{\circ}$,$\angle BAC = 40^{\circ}$,所以$\angle ABD = 70^{\circ}- 30^{\circ}=10^{\circ}$,即$\angle CBD = 10^{\circ}$。
【答案】:
(1) C;(2) D;(3) B;(4) B
(1) 本题考察的是三角形三边关系“两边之和大于第三边,两边之差小于第三边”。
已知两边长分别是2和4,设第三边长为$x$,根据三角形三边关系可得:
$4 - 2 \lt x \lt 4 + 2$,即$2 \lt x \lt 6$。
逐一分析选项:
选项A:$1\lt 2$,不满足$2 \lt x \lt 6$,所以A选项错误。
选项B:$2 = 2$,不满足$2 \lt x \lt 6$,所以B选项错误。
选项C:$2\lt 5\lt 6$,满足$2 \lt x \lt 6$,所以C选项正确。
选项D:$6 = 6$,不满足$2 \lt x \lt 6$,所以D选项错误。
(2) 本题可根据全等三角形的判定定理,逐一分析每个选项。
选项A:周长相等的两个锐角三角形,只能说明它们三边之和相等,但三边的长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个锐角三角形不一定全等,A选项错误。
选项B:周长相等的两个直角三角形,同样只能说明三边之和相等,三边长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个直角三角形不一定全等,B选项错误。
选项C:周长相等的两个等腰三角形,只能确定两腰与底边之和相等,但两腰和底边的长度不一定对应相等,不满足全等三角形的判定条件,所以周长相等的两个等腰三角形不一定全等,C选项错误。
选项D:因为等边三角形的三边都相等,周长相等的两个等边三角形,其三边长度必然对应相等。
根据全等三角形判定定理“边边边”(SSS),三边对应相等的两个三角形全等,所以周长相等的两个等边三角形全等,D选项正确。
(3) 本题可根据全等三角形的判定定理,结合已知条件$BE\perp AC$,$CF\perp AB$,$BE = CF$,找出图中的全等三角形。
已知$BE\perp AC$,$CF\perp AB$,则$\angle AEB=\angle AFC = 90^{\circ}$。
在$\triangle ABE$和$\triangle ACF$中:
$\begin{cases} \angle AEB=\angle AFC,\\ \angle BAE=\angle CAF,\\ BE = CF. \end{cases}$
根据全等三角形判定定理“角角边”(AAS),可得$\triangle ABE\cong\triangle ACF$。
因为$AB = AC$(由$\triangle ABE\cong\triangle ACF$可得),$BE\perp AC$,$CF\perp AB$,$BE = CF$,在$\triangle BCE$和$\triangle CBF$中:
$\begin{cases} \angle BEC=\angle CFB = 90^{\circ},\\ BC = CB,\\ BE = CF. \end{cases}$
根据全等三角形判定定理“斜边直角边”(HL),可得$\triangle BCE\cong\triangle CBF$。
所以图中全等三角形有$\triangle ABE\cong\triangle ACF$,$\triangle BCE\cong\triangle CBF$,共$2$对,B选项正确。
(4) 本题可先根据等腰三角形的性质求出$\angle ACB$的度数,再根据折叠的性质得到相关角的关系,进而求出$\angle CBD$的度数。
因为$AC = BC$,$\angle BAC = 40^{\circ}$,根据等腰三角形两底角相等以及三角形内角和为$180^{\circ}$,可得:
$\angle ABC=\angle ACB=\frac{1}{2}×(180^{\circ}-\angle BAC)=\frac{1}{2}×(180^{\circ} - 40^{\circ}) = 70^{\circ}$。
由折叠的性质可知:$\triangle ABC\cong\triangle ADC$,所以$\angle D=\angle ABC = 70^{\circ}$,$BC = DC$。
因为$BC = DC$,所以$\angle CBD=\angle D = 70^{\circ}$。
在$\triangle BCD$中,$\angle CBD=\angle D = 70^{\circ}$,根据三角形内角和为$180^{\circ}$,可得:
$\angle BCD=180^{\circ}-2×70^{\circ}= 40^{\circ}$。
则$\angle ABD=\angle ABC-\angle CBD=70^{\circ}- \angle CBD$。
又因为$\angle ABC = 70^{\circ}$,$\angle BCD = 40^{\circ}$,$\angle BAC = 40^{\circ}$,所以$\angle ABD = 70^{\circ}- 30^{\circ}=10^{\circ}$,即$\angle CBD = 10^{\circ}$。
【答案】:
(1) C;(2) D;(3) B;(4) B