2. (1) 如图,作CE⊥AB,DF⊥AB,垂足分别为E,F.
① 已知AC//DB,且AC= DB,则△ACE≌△BDF,根据
② 已知AC//DB,且AE= BF,则△ACE≌△BDF,根据
③ 已知AE= BF,且CE= DF,则△ACE≌△BDF,根据
④ 已知AC= BD,CE= DF(或AE= BF),则△ACE≌△BDF,根据
(2) 如图,点Q在∠AOB的平分线上,QA⊥OA,QB⊥OB,垂足分别为A,B,则AQ=
(3) 如图,AB垂直平分CD,AC= 6 cm,BD= 4 cm,四边形ABCD的周长为
① 已知AC//DB,且AC= DB,则△ACE≌△BDF,根据
AAS
;② 已知AC//DB,且AE= BF,则△ACE≌△BDF,根据
ASA
;③ 已知AE= BF,且CE= DF,则△ACE≌△BDF,根据
HL
;④ 已知AC= BD,CE= DF(或AE= BF),则△ACE≌△BDF,根据
HL或AAS
;(2) 如图,点Q在∠AOB的平分线上,QA⊥OA,QB⊥OB,垂足分别为A,B,则AQ=
BQ
,理由是角平分线上的点到角两边的距离相等
;(3) 如图,AB垂直平分CD,AC= 6 cm,BD= 4 cm,四边形ABCD的周长为
20
cm.答案:【解析】:
(1)
① 已知$AC// DB$,且$AC = DB$,$CE\perp AB$,$DF\perp AB$,所以$\angle A=\angle B$(两直线平行,内错角相等),又$AC = DB$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“角角边”($AAS$),可得$\triangle ACE\cong\triangle BDF$。
② 已知$AC// DB$,则$\angle A=\angle B$(两直线平行,内错角相等),又$AE = BF$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“角边角”($ASA$),可得$\triangle ACE\cong\triangle BDF$。
③ 已知$AE = BF$,则$AE + EF=BF + EF$,即$AF = BE$,又$CE = DF$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“斜边直角边”($HL$),可得$\triangle ACE\cong\triangle BDF$。
④ 已知$AC = BD$,$CE = DF$(或$AE = BF$),$CE\perp AB$,$DF\perp AB$,所以$\angle AEC=\angle BFD = 90^{\circ}$,根据“斜边直角边”($HL$)(当$CE = DF$时)或通过$AE = BF$,$\angle AEC=\angle BFD = 90^{\circ}$,$AC = BD$,根据“角角边”($AAS$)(当$AE = BF$时),可得$\triangle ACE\cong\triangle BDF$。
(2) 因为点$Q$在$\angle AOB$的平分线上,$QA\perp OA$,$QB\perp OB$,根据角平分线上的点到角两边的距离相等,所以$AQ = BQ$。
(3) 因为$AB$垂直平分$CD$,所以$AC = AD = 6cm$,$BC = BD = 4cm$,则四边形$ABCD$的周长为$AC + AD+BC + BD=6 + 6+4 + 4=20cm$。
【答案】:
(1)
① $AAS$;
② $ASA$;
③ $HL$;
④ $HL$或$AAS$;
(2) $BQ$;角平分线上的点到角两边的距离相等;
(3) $20$。
(1)
① 已知$AC// DB$,且$AC = DB$,$CE\perp AB$,$DF\perp AB$,所以$\angle A=\angle B$(两直线平行,内错角相等),又$AC = DB$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“角角边”($AAS$),可得$\triangle ACE\cong\triangle BDF$。
② 已知$AC// DB$,则$\angle A=\angle B$(两直线平行,内错角相等),又$AE = BF$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“角边角”($ASA$),可得$\triangle ACE\cong\triangle BDF$。
③ 已知$AE = BF$,则$AE + EF=BF + EF$,即$AF = BE$,又$CE = DF$,$\angle AEC=\angle BFD = 90^{\circ}$,根据“斜边直角边”($HL$),可得$\triangle ACE\cong\triangle BDF$。
④ 已知$AC = BD$,$CE = DF$(或$AE = BF$),$CE\perp AB$,$DF\perp AB$,所以$\angle AEC=\angle BFD = 90^{\circ}$,根据“斜边直角边”($HL$)(当$CE = DF$时)或通过$AE = BF$,$\angle AEC=\angle BFD = 90^{\circ}$,$AC = BD$,根据“角角边”($AAS$)(当$AE = BF$时),可得$\triangle ACE\cong\triangle BDF$。
(2) 因为点$Q$在$\angle AOB$的平分线上,$QA\perp OA$,$QB\perp OB$,根据角平分线上的点到角两边的距离相等,所以$AQ = BQ$。
(3) 因为$AB$垂直平分$CD$,所以$AC = AD = 6cm$,$BC = BD = 4cm$,则四边形$ABCD$的周长为$AC + AD+BC + BD=6 + 6+4 + 4=20cm$。
【答案】:
(1)
① $AAS$;
② $ASA$;
③ $HL$;
④ $HL$或$AAS$;
(2) $BQ$;角平分线上的点到角两边的距离相等;
(3) $20$。
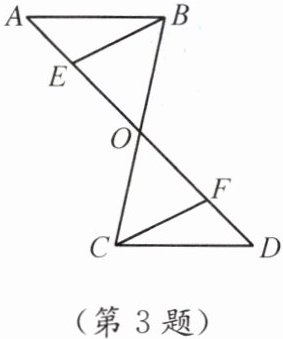
3. 如图,AB//CD,O是BC的中点,BE//CF,BE,CF分别交AD于点E,F.
(1) 求证:BE= CF.
(2) 图中共有几组全等三角形?请把它们都写出来.
(1) 求证:BE= CF.
(2) 图中共有几组全等三角形?请把它们都写出来.

答案:
(1)证明:
∵AB//CD,
∴∠A=∠D,∠ABE=∠DCF,
∵O是BC的中点,
∴BO=CO,
∵BE//CF,
∴∠BEO=∠CFO,∠EBO=∠FCO,
在△BEO和△CFO中,
∠BEO=∠CFO,∠EBO=∠FCO,BO=CO,
∴△BEO≌△CFO(AAS),
∴BE=CF;
(2)解:图中共有2组全等三角形,分别是△BEO≌△CFO,△ABE≌△DCF.
(1)证明:
∵AB//CD,
∴∠A=∠D,∠ABE=∠DCF,
∵O是BC的中点,
∴BO=CO,
∵BE//CF,
∴∠BEO=∠CFO,∠EBO=∠FCO,
在△BEO和△CFO中,
∠BEO=∠CFO,∠EBO=∠FCO,BO=CO,
∴△BEO≌△CFO(AAS),
∴BE=CF;
(2)解:图中共有2组全等三角形,分别是△BEO≌△CFO,△ABE≌△DCF.
4. 如图,已知线段c,求作等腰直角三角形,使其斜边等于线段c(保留作图痕迹,不必写作法).


答案:【解析】:本题考查了等腰直角三角形的性质以及作一条线段等于已知线段。我们需要利用已知的线段c,通过构造直角,并利用等腰直角三角形的性质(两直角边相等)来作出满足条件的三角形。
【答案】:解:
图略。
作法:①作线段$AB=c$。
②作$AB$的垂直平分线$MN$,垂足为$D$。
③以$D$为圆心,$\frac{1}{2}AB$长为半径作弧,交$MN$于点$C$。
④连接$AC$,$BC$。
则$\bigtriangleup ABC$就是所求作的等腰直角三角形。
【答案】:解:
图略。
作法:①作线段$AB=c$。
②作$AB$的垂直平分线$MN$,垂足为$D$。
③以$D$为圆心,$\frac{1}{2}AB$长为半径作弧,交$MN$于点$C$。
④连接$AC$,$BC$。
则$\bigtriangleup ABC$就是所求作的等腰直角三角形。